度量学习（metric learning）

转自：http://blog.csdn.net/nehemiah_li/article/details/44230053

度量学习（Metric Learning）

度量（Metric）的定义 

在数学中，一个度量（或距离函数）是一个定义集合中元素之间距离的函数。一个具有度量的集合被称为度量空间。

1 为什么要用度量学习？

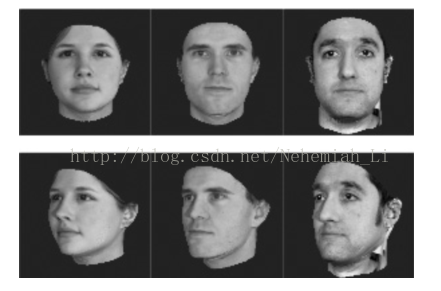
很多的算法越来越依赖于在输入空间给定的好的度量。例如K-means、K近邻方法、SVM等算法需要给定好的度量来反映数据间存在的一些重要关系。这一问题在无监督的方法（如聚类）中尤为明显。举一个实际的例子，考虑图1的问题，假设我们需要计算这些图像之间的相似度（或距离，下同）（例如用于聚类或近邻分类）。面临的一个基本的问题是如何获取图像之间的相似度，例如如果我们的目标是识别人脸，那么就需要构建一个距离函数去强化合适的特征（如发色，脸型等）；而如果我们的目标是识别姿势，那么就需要构建一个捕获姿势相似度的距离函数。为了处理各种各样的特征相似度，我们可以在特定的任务通过选择合适的特征并手动构建距离函数。然而这种方法会需要很大的人工投入，也可能对数据的改变非常不鲁棒。度量学习作为一个理想的替代，可以根据不同的任务来自主学习出针对某个特定任务的度量距离函数。

 

图 1

2 度量学习的方法

根据相关论文[2，3，4]，度量学习方法可以分为通过线性变换的度量学习和度量学习的非线性模型。

2.1 通过线性变换的度量学习

由于线性度量学习具有简洁性和可扩展性(通过核方法可扩展为非线性度量方法)，现今的研究重点放在了线性度量学习问题上。线性的度量学习问题也称为马氏度量学习问题，可以分为监督的和非监督的学习算法。

监督的马氏度量学习可以分为以下两种基本类型:

I 监督的全局度量学习：该类型的算法充分利用数据的标签信息。如

 

• Information-theoretic metric learning(ITML)
• Mahalanobis Metric Learning for Clustering([1]中的度量学习方法，有时也称为MMC)
• Maximally Collapsing Metric Learning (MCML)

 

II 监督的局部度量学习：该类型的算法同时考虑数据的标签信息和数据点之间的几何关系。如

 

• Neighbourhood Components Analysis (NCA)
• Large-Margin Nearest Neighbors (LMNN)
• Relevant Component Analysis(RCA)
• Local Linear Discriminative Analysis(Local LDA)

 

此外，一些很经典的非监督线性降维算法可以看作属于非监督的马氏度量学习。如

•  主成分分析(Pricipal Components Analysis, PCA)
• 多维尺度变换(Multi-dimensional Scaling, MDS)
• 非负矩阵分解(Non-negative Matrix Factorization,NMF)
• 独立成分分析(Independent components analysis, ICA)
• 邻域保持嵌入(Neighborhood Preserving Embedding,NPE)
• 局部保留投影(Locality Preserving Projections. LPP)

 

2.2 度量学习的非线性模型

非线性的度量学习更加的一般化，非线性降维算法可以看作属于非线性度量学习。经典的算法有等距映射(Isometric Mapping,ISOMAP) 、局部线性嵌入(Locally Linear Embedding, LLE) ，以及拉普拉斯特征映射(Laplacian Eigenmap，LE ) 等。另一个学习非线性映射的有效手段是通过核方法来对线性映射进行扩展。此外还有如下几个方面

 

• Non-Mahalanobis Local Distance Functions
• Mahalanobis Local Distance Functions
• Metric Learning with Neural Networks

3 应用

度量学习已应用于计算机视觉中的图像检索和分类、人脸识别、人类活动识别和姿势估计，文本分析和一些其他领域如音乐分析，自动化的项目调试，微阵列数据分析等[4]。

推荐阅读的论文

以下列举的论文大都对后来度量学习产生了很大影响（最高的google引用量上了5000次）。1-6篇论文是关于一些方法的论文，最后一篇为综述。

 

• Distance metric learning with application to clustering with side-information
• Information-theoretic metric learning(关于ITML)
• Distance metric learning for large margin nearest neighbor classification(关于LMNN)
• Learning the parts of objects by non-negative matrix factorization（Nature关于RCA的文章）
• Neighbourhood components analysis(关于NCA)
• Metric Learning by Collapsing Classes(关于MCML)
• Distance metric learning a comprehensive survey(一篇经典的综述)

机器学习数据集

UCI machine learning repository：http://archive.ics.uci.edu/ml/

 

 

参考文献

[1] Xing E P, Jordan M I, Russell S, et al. Distance metric learning with application to clustering with side-information[C]//Advances in neural information processing systems. 2002: 505-512.

[2] Kulis B. Metric learning: A survey[J]. Foundations and Trends in Machine Learning, 2012, 5(4): 287-364.

[3] Yang L, Jin R. Distance metric learning: A comprehensive survey[J]. Michigan State Universiy, 2006, 2.

[4]王微. 融合全局和局部信息的度量学习方法研究[D]. 中国科学技术大学, 2014.