【数据结构 顺序表】超详细理解&&例题&&错题

已于 2024-10-24 17:51:33 修改
阅读量1.3k 收藏 23
点赞数 23
分类专栏： 数据结构 文章标签： 1024程序员节 visual studio c语言 数据结构 html 算法
于 2024-10-24 17:17:21 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/Sunfor_sun/article/details/143130054
版权

数据结构 顺序表

你好，这里是新人 Sunfor

这篇是我最近对于数据结构 顺序表的学习心得和错题整理
有任何错误欢迎指正，欢迎交流！
会持续更新，希望对你有所帮助，我们一起学习，一起进步

前言

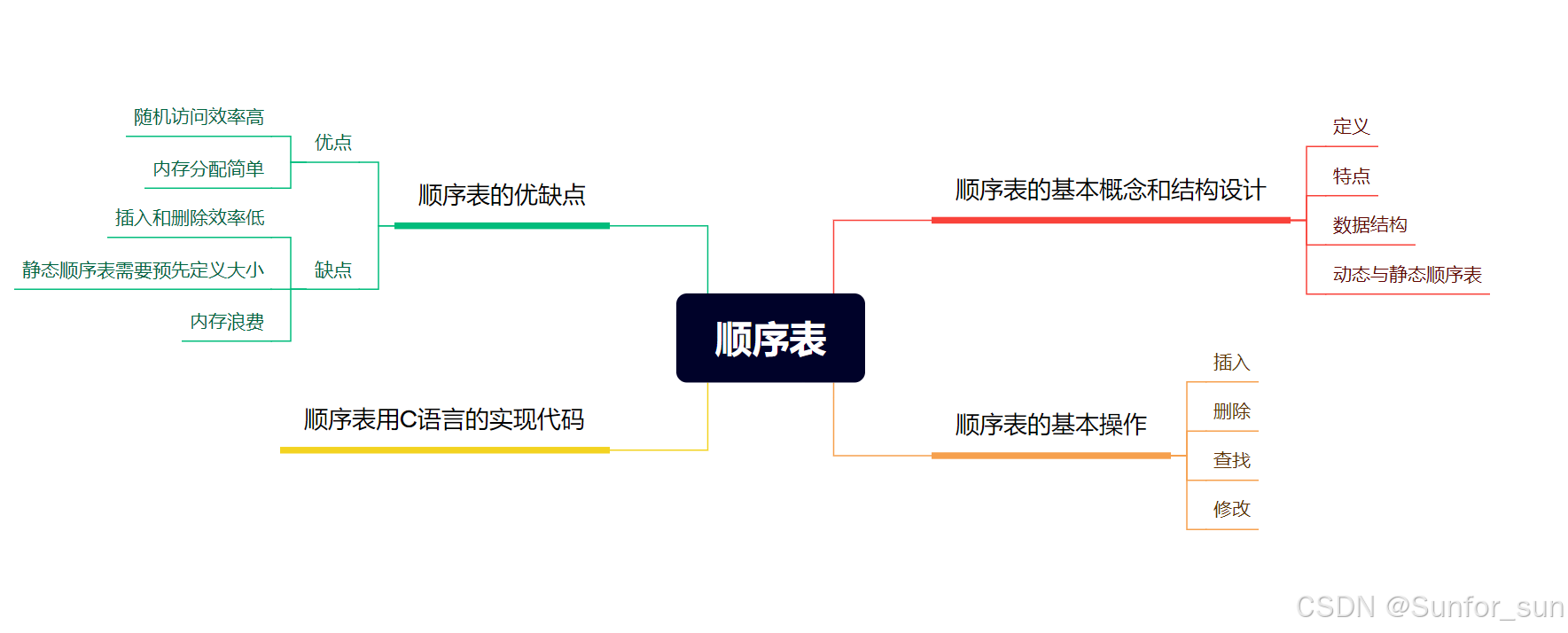
在这里插入图片描述

一、顺序表的基本概念和结构设计

1.线性表

在介绍顺序表之前，我们先要了解什么是 线性表
线性表是n个具有相同特性的数据元素的有限序列。线性表是一种在实际中广泛使用的的数据结构
常见的线性表：顺序表、链表、栈、队列、字符串
线性表在逻辑上是线性结构，也就是说是连续的一条直线
但是在物理结构上并不一定是连续的，线性表在物理上存储时，通常以数组和链式结构的形式存储

2.顺序表的概念

顺序表是一种线性表的存储结构，它将线性表的元素按照顺序存放在一段连续的内存空间中（物理地址连续），一般情况下采用数组存储
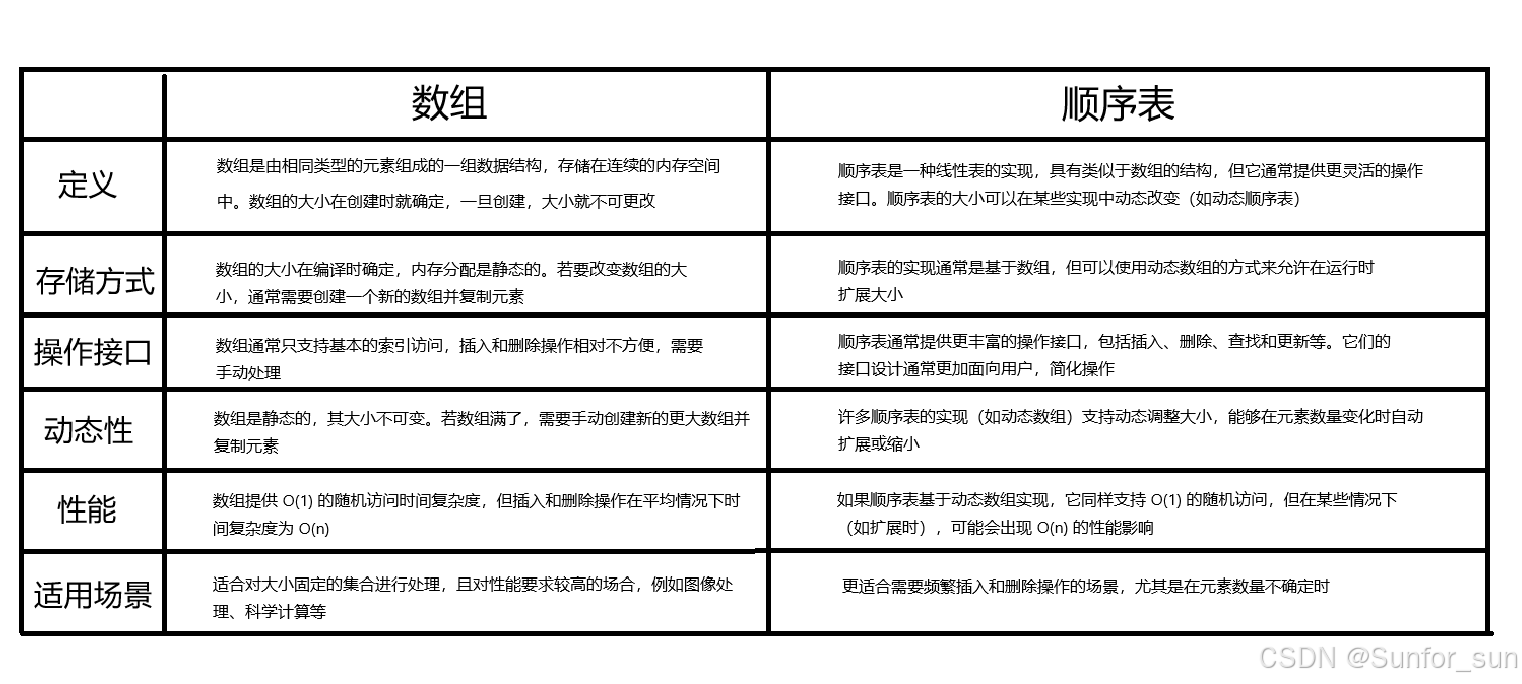
在这里插入图片描述
顺序表和数组的区别在哪呢？
首先 顺序表绝对不等于数组
我们来结合图像理解一下：
在这里插入图片描述
简单来理解：
数组类似于苍蝇馆子 顺序表类似于米其林餐厅

3.顺序表的结构

顺序表的结构体设计通常包括：存储数据的数组指针、当前元素的个数以及顺序表的最大容量

#include<stdio.h>
#include<stdlib.h>

typedef struct
{
   int* data;//存储元素的动态数组指针
   int length;//当前元素个数
   int capacity;//最大容量
}SeqList;

4.顺序表的分类

静态顺序表

使用定长数组存储元素
在这里插入图片描述
缺点：使用定长数组，给少了造成不够用，给多了造成空间浪费

动态顺序表

在这里插入图片描述
动态顺序表可以根据需要 自动扩展或缩小，减少了内存的浪费
动态顺序表支持随机访问，能够在常数时间内通过索引访问任何元素

二、顺序表的基本操作

初始化、插入、删除、查找、更新、遍历
我们等会儿在顺序表的实现中就会展示

三、顺序表的代码实现

在实现之前我们也需要合理使用多文件操作
例如扫雷这篇博客，我们需要建立3个文件

  • SeqList.h :存放整个程序需要的声明，同时也类似于目录的作用
  • SeqList.c :所需函数的定义
  • text.c :函数的具体实现，以及主函数

SeqList.h

#include<stdio.h>
#include<stdlib.h>
#include<assert.h>

//定义一个动态顺序表的结构
typedef int SLDatatype;//不确定具体的数据类型，先定义一个SLDatatype 方便后面的修改

typedef struct SqList{
	SLDatatype* arr;//动态数组，存储顺序表元素
	int capacity;//记录当前空间的大小
	int size;//有效数据的个数
}SL;//定义一个更好记的名字

//初始化
void SLInit(SL* ps);

//销毁
void SLDestory(SL* ps);

//打印
void SLPrint(SL* ps);

//插入数据
void SLPushBack(SL* ps,SLDatatype x);//尾插
void SLPushFront(SL* ps,SLDatatype x);//头插

//删除
void SLPopBack(SL* ps);//尾删
void SLPopFront(SL* ps);//头删

//在指定位置之前插入数据
void SLInsert(SL* ps,SLDatatype x,int pos);

//删除指定位置的数据
void SLErase(SL* ps,int pos);

//查找数据
int SLFind(SL* ps,SLDatatype x);

SeqList.c

#include"SeqList.h"

//初始化
void SLInit(SL* ps)
{
	ps->arr = NULL;//初始化数组指针为NULL,表示当前没有分配内存
	ps->size = ps->capacity = 0;//有效元素个数和容量初始化为0，表示顺序表为空且尚未分配空间
}

//销毁
void SLDestory(SL* ps)
{
	if(ps->arr)//相当于ps->arr != NULL
	{
		free(ps->arr);
	}
	ps->arr = NULL;
	ps->capacity = ps->size = 0;
}

//打印顺序表
void SLPrint(SL* ps)
{
	for(int i = 0;i < ps->size;i++)
	{
		printf("%d ",ps->arr[i]);
	}
	printf("\n");
}

//检查空间是否足够
void SLCheckCapacity(SL* ps)
{
	if(ps->size == ps->capacity)//空间不足
	{
		//增容
		//若capacity=0，就先给个默认值，否则*2
		int newCapacity = ps->capacity == 0?4:2* ps->capacity;

		//动态申请一块空间
		SLDatatype* tmp = ps->arr = (SLDatatype*)realloc(ps->arr,newCapacity* sizeof(SLDatatype));
		if(tmp ==NULL)
		{
			perror("realloc fail!");
			exit(1);
		}
		//更新数据
		ps->arr = tmp;
		ps->capacity = newCapacity;
	}
}

//尾插
void SLPushBack(SL* ps,SLDatatype x)
{
	assert(ps);//传入的指针不能为空
	SLCheckCapacity(ps);
	ps->arr[ps->size++] = x;//将元素添加到数组末尾，并增加有效元素个数
}

//头插
void SLPushFront(SL* ps,SLDatatype x)
{
	assert(ps);
	SLCheckCapacity(ps);
	for(int i = ps->size;i > 0;i--)//从当前顺序表的最后一个有效元素开始，向前移动元素，为插入新元素腾出空间，
	{
		ps->arr[i] = ps->arr[i - 1];
	}
	//下标为0的位置空出来
	ps->arr[0] = x;
	//插入之后size也后移
	ps->size++;
}

举个例子方便大家理解

//尾删
void SLPopback(SL* ps)
{
	//说明顺序表不为空
	assert(ps);
	assert(ps->size);

	//把最后一个数据删掉
	//ps->arr[ps->size - 1] = -1;//多余了
	ps->size--;//虽然后面有数据，但不是有效数据，对后续的计算不影响，新的数据会直接覆盖上去
}

在这里插入图片描述

//头删
void SLPopFront(SL* ps)
{
	assert(ps);
	assert(ps->size);


    //数据整体向前挪动一位
	for (int i = 0;i<ps->size-1; i++)
	{
		ps->arr[i] = ps->arr[i + 1];//i = size -2
	}
	//删除一个数据size前移
	ps->size--;
}

在这里插入图片描述

//在指定位置之前插入数据
void SLInsert(SL* ps, SLDatatype x, int pos)
{
	assert(ps);
	//         = 头插          = 尾插
	assert(pos >= 0 && pos <= ps->size);
	//判断空间是否足够
	SLCheckCapacity(ps);

	//pos及之后的数据整体向后移一位
	for (int i = ps->size; i > pos; i--)
	{
		ps->arr[i] = ps->arr[i - 1];//pos+1 -> pos
	}

	ps->arr[pos] = x;
	ps->size++;
}

在这里插入图片描述

// 删除指定位置的数据
void SLErase(SL* ps, int pos)
{
	assert(ps);
	//                 不能= size为最后一个数据
	assert(pos >= 0 && pos < ps->size);
	for (int i = pos;i < ps->size-1;i++)
	{
		ps->arr[i] = ps->arr[i + 1];//size - 2 <- size -1
	}
	ps->size--;
}

在这里插入图片描述

//查找数据
int SLFind(SL* ps, SLDatatype x)
{
	assert(ps);
	for (int i = 0; i < ps->size; i++)
	{
		if (ps->arr[i] == x) 
		{
			return i;
		}
	}
	//没有找到：返回一个无效的下标
	return -1;
}

text.c

#include"SeqList.h"

void SLtest01()
{
	SL s;

	SLInit(&s);//得把地址传过去 值才会改变

	SLPushBack(&s, 1);
	SLPushBack(&s, 2);
	SLPushBack(&s, 3);
	SLPushBack(&s, 4);

	//SLPushFront(&s, 1);
	//SLPushFront(&s, 2);
	//SLPushFront(&s, 3);
	//SLPushFront(&s, 4);

	SLPrint(&s);//1 2 3 4

	//SLPopback(&s);
	//SLPrint(&s);
	//SLPopback(&s);
	//SLPrint(&s);
	//SLPopback(&s);
	//SLPrint(&s);
	//SLPopback(&s);
	//SLPrint(&s);
	//为空就不能再删

	//SLPopFront(&s);
	//SLPrint(&s);
	//SLPopFront(&s);
	//SLPrint(&s);
	//SLPopFront(&s);
	//SLPrint(&s);
	//SLPopFront(&s);
    //SLPrint(&s);
	//不能对空顺序表继续删除

	//SLInsert(&s, 11, 0);
	//SLPrint(&s);
	//SLInsert(&s, 22, s.size);
	//SLPrint(&s);
	//SLInsert(&s, 33, 2);
	//SLPrint(&s);

	//SLErase(&s, 0);
	//SLPrint(&s);
	//SLErase(&s, s.size-1);
	//SLPrint(&s);
	//SLErase(&s, 1);
	//SLPrint(&s);

	SLFind(&s, 2);

	int find = SLFind(&s, 222);
	if (find < 0)
	{
		printf("没找到！\n");
	}
	else
	{
		printf("找到了！\n");
	}

	SLDestory(&s);
}

int main()
{
	SLtest01();
	
	return 0;
}
  • 注意，在顺序表的实现过程中，我们还是要常用调试，这样更容易发现错误，也方便我们去理解

四、顺序表的优缺点

1.优点

  • 随机访问：顺序表允许 O(1) 时间复杂度的随机访问，可以直接通过索引访问任何元素。
  • 内存局部性：顺序表中的元素存储在连续的内存地址中，有助于提高缓存命中率，进而提升访问速度。
  • 简单实现：顺序表的实现相对简单，常用操作（如插入、删除、遍历）易于理解和实现。
  • 空间效率：在没有太多插入和删除操作的情况下，顺序表的空间利用效率较高，因为其元素是连续存储的。
  • 动态扩展：许多实现支持动态扩展，能够在需要时自动增加容量，适应不同大小的需求。
  • 简化的内存管理：相较于链表，顺序表的内存管理较为简单，通常只需一次性申请一块内存即可。
  • 易于实现算法：某些算法（如排序、查找等）在顺序表上实现时，往往更加高效和简洁。

2.缺点

  • 固定容量：在创建时通常需要指定初始容量，若超出容量需进行扩展，扩展过程可能导致性能下降。
  • 插入和删除效率低：在中间位置插入或删除元素时，需要移动大量元素，时间复杂度为 O(n)。
  • 内存浪费：为了避免频繁扩展，可能会预留额外的内存，这在某些情况下可能导致空间浪费。
  • 不支持复杂数据结构：顺序表适合存储简单数据，处理复杂对象时，灵活性较差。
  • 数据类型限制：在一些语言中，顺序表要求所有元素为同一数据类型，限制了灵活性。

五、顺序表的算法题整理

顺序表的合并
题目要求：
给你两个按非递减顺序排列的整数数组 nums1 和 nums2，另有两个整数 m 和 n ，分别表示 nums1 和 nums2 中的元素数目。
请你合并 nums2 到 nums1 中，使合并后的数组同样按 非递减顺序 排列。
注意：最终，合并后数组不应由函数返回，而是存储在数组 nums1 中。为了应对这种情况，nums1 的初始长度为 m + n，其中前 m 个元素表示应合并的元素，后 n 个元素为 0 ，应忽略。nums2 的长度为 n

如果用顺序表去做这道题我们该怎么去考虑呢
首先顺序表的 底层逻辑是数组，所以我们先用数组去解决这道题目
给定两个数组，分别给定三个指针，一个指向第一个数组的最后一个元素，一个指向第二个数组的最后一个元素，一个指向两个数组合并后的数组的最后一个元素

void merge(int* nums1, int nums1Size, int m, int* nums2, int nums2Size, int n) {
    int l1 = m - 1;//nums1的有效元素最后一个索引
    int l2 = n - 1;//nums2的有效元素最后一个索引
    int l3 = m + n - 1;// 合并后数组的最后一个索引

    while (l1 >= 0 && l2 >= 0)
    {
        if (nums1[l1] > nums2[l2])
        {
            nums1[l3--] = nums1[l1--];//将较大的元素放在合并后数组
        }
        else
        {
            nums1[l3--] = nums2[l2--];//将较大的元素放在合并后数组
        }
    }

    while (l2 >= 0)
    {
        nums1[l3--] = nums2[l2--];//如果nums2还有剩余元素，将其放在nums1中
    }
}

那如果我们使用 顺序表 去解决类似的问题呢
已知顺序表L1和L2中数据均由小到大排序，请用尽可能快的方法将L1与L2中的数据合并到L3中，使数据在L3中按升序排列

#include <stdio.h>
#include <stdlib.h>

#define MAXSIZE 100

typedef struct {
    int data[MAXSIZE];
    int length;
} SQList;

void init(SQList* L);
void print(const SQList* L);
void merge(const SQList* L1, const SQList* L2, SQList* L3);

int main() {
    SQList L1, L2, L3;

    // 初始化 L1 和 L2
    printf("初始化线性表 L1:\n");
    init(&L1);
    
    printf("初始化线性表 L2:\n");
    init(&L2);

    // 合并 L1 和 L2 到 L3
    merge(&L1, &L2, &L3);

    // 打印合并后的线性表 L3
    printf("合并后的线性表 L3:\n");
    print(&L3); 

    return 0;
}

// 初始化线性表
void init(SQList* L) {
    printf("请输入线性表的长度 (最多 %d): ", MAXSIZE);
    scanf("%d", &(L->length));

    // 确保长度不超过 MAXSIZE
    if (L->length > MAXSIZE) {
        L->length = MAXSIZE;
        printf("输入长度超过最大值，已设置为 %d。\n", MAXSIZE);
    }

    printf("请输入线性表的数据（要求有序）:\n");
    for (int i = 0; i < L->length; i++) {
        printf("元素 %d: ", i + 1);
        scanf("%d", &(L->data[i]));
    }
}

// 合并两个有序线性表
void merge(const SQList* L1, const SQList* L2, SQList* L3) {
    int i = 0, j = 0, k = 0;

    // 合并过程
    while (i < L1->length && j < L2->length) {
        if (L1->data[i] < L2->data[j]) {
            L3->data[k++] = L1->data[i++];
        } else {
            L3->data[k++] = L2->data[j++];
        }
    }

    // 复制剩余元素
    while (i < L1->length) {
        L3->data[k++] = L1->data[i++];
    }
    while (j < L2->length) {
        L3->data[k++] = L2->data[j++];
    }

    // 设置 L3 的长度
    L3->length = k; 
}

// 打印线性表数据
void print(const SQList* L) {
    printf("线性表的数据: ");
    for (int i = 0; i < L->length; i++) {
        printf("%d ", L->data[i]);
    }
    printf("\n"); // 打印换行
}

顺序表的奇偶数划分
尽可能快地将顺序表L中的所有奇数调整到表的左边，所有偶数调整到表的右边

首先我们要将左边的偶数和右边的奇数都找出来，再进行交换

#include <stdio.h>
#include <stdlib.h>

typedef struct {
    int *data;
    int length;
} sequence_list;

// 初始化线性表
void init(sequence_list *L, int n) {
    L->data = (int *)malloc(n * sizeof(int));
    L->length = n;
    for (int i = 0; i < n; i++) {
        scanf("%d", &L->data[i]);
    }
}

// 输出线性表
void Print(sequence_list *L) {
    for (int i = 0; i < L->length; i++) {
        printf("%d", L->data[i]);
        if (i < L->length - 1) {
            printf(" ");
        }
    }
    printf("\n");
}

// 重新排列奇偶数
void partition(sequence_list *L) {
    int left = 0, right = L->length - 1;
    while (left < right) {
        // 找到左边的偶数
        while (left < right && L->data[left] % 2 != 0) {
            left++;
        }
        // 找到右边的奇数
        while (left < right && L->data[right] % 2 == 0) {
            right--;
        }
        // 交换
        if (left < right) {
            int temp = L->data[left];
            L->data[left] = L->data[right];
            L->data[right] = temp;
        }
    }
}

int main() {
    int n;
    scanf("%d", &n);
    
    sequence_list L;
    init(&L, n);
    
    partition(&L);
    
    Print(&L);
    
    // 释放内存
    free(L.data);
    
    return 0;
}

顺序表的学习我们先在此告一段落，之后在学习数据结构的过程中还会有顺序表的补充内容随机掉落，其他数据结构的相关知识也会陆续更新，大家可以持续关注~

评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值