【凸优化笔记一】仿射集+凸集+锥

引言

最近开始接触凸优化问题，发现自己这块知识点处于零散的认知阶段，所以配合着哔站上的课程，以及相应配套的书籍进行学习。
哔站链接传送门：中科大-凸优化
推荐的书籍有以下三本：
Convex Optimization Stephen Boyd, Lieven Vandenberghe
Nonlinear Programming, Second Edition Dimitri Bertsekas
Parallel and Distributed Computation:Numerical Methods Dimitri Bersekas, John Tsitsiklis

接下来的学习以及引用也主要来自于这三本书。

直线&线段

直线和线段是我们自从接触小学初中的几何问题以来，最常见也是最基本的概念，为什么在这里还需要重新提一下这两个概念呢？
首先，正是因为其基础，方便大家形成螺旋式上升的模式；其次，这两个概念必然为后续的一些概念打下了铺垫和引理的作用；最后，请用数学的语言来表达高维空间上的直线和线段的定义。（这里思考片刻，曾经在初高中时期，我们应该是学习过二维平面上的直线的定义的吧，试试能够完整的写下来）

直线的定义

$$\begin{array}{c}\{\begin{array}{lr}{X}_1\ne X_2\in R^n,& \\ \theta \in R,& \\ Y=\theta X_1+(1-\theta )X_2=X_2+\theta (X_1-X_2),& \end{array}\end{array}$$

线段的定义

由于线段是直线的一部分，所以仅需在直线的定义下稍加限制即可满足线段定义
$$\begin{array}{c}\{\begin{array}{lr}{X}_1\ne X_2\in R^n,& \\ \theta \in R,\theta \in [0,1]& \\ Y=\theta X_1+(1-\theta )X_2=X_2+\theta (X_1-X_2),& \end{array}\end{array}$$

仿射集 Affine Sets

正式进入正文，仿射集，有以下定义形式
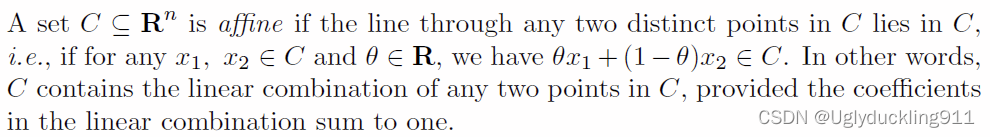一个集合C是仿射集，若$\forall X_1,X_2\in C$，则连接$X_1,X_2$的直线也在集合中；换言之，线性组合两点（可以思考成向量）依然在集合C中。
以上定义，可被扩大为$X_1,...,X_k$的仿射组合。

与C相关的子空间

由于往往在现实问题中，当得到某仿射集后，认为性质不够好，可以通过减掉其集合中的一个元素，即可获得与C相关的子空间，V。由此不再收到仿射集定义中1的限制。
以下是定义及其证明

线性方程组的解集是仿射集

以下是证明过程
上图中最后一句也说明了，小标题是一充分必要条件。

零空间

结合以上的与C相关的子空间V以及线性方程组的解集是仿射集，可以有以下推演

值得注意的是，V中任意元素都是A的零空间。

仿射包 Affine Hull

任意集合C，构成尽可能小的仿射集，即为仿射包

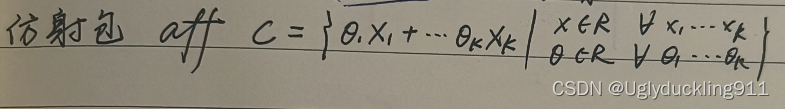
凸集 Convex Set

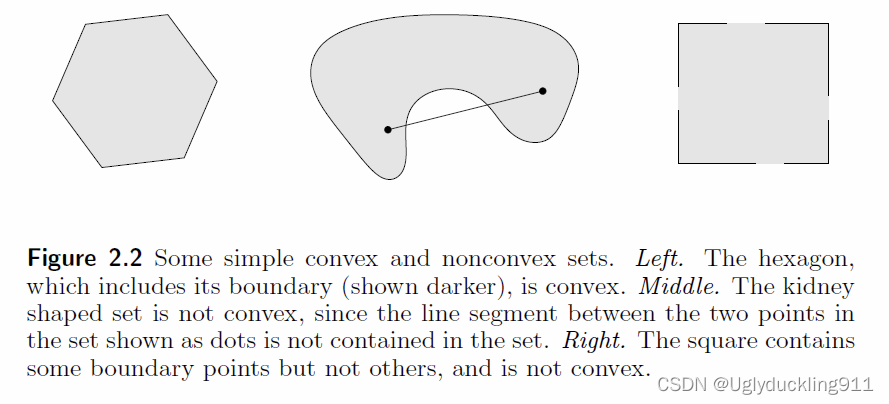
一个集合C是凸集，当任意两点之间的线段仍在C内。

其中，值得注意的是，仿射集是凸集的特例。以二维平面上的一个圆为例，不难发现，圆是凸集，但不是仿射集。这里可以简易的认为，需要满足凸集的要求比仿射集低，所以仿射集是凸集的特例，仿射集一定是凸集，凸集不一定是仿射集。从定义角度的需要包含的直线和线段中，也可以说明两者的关系。

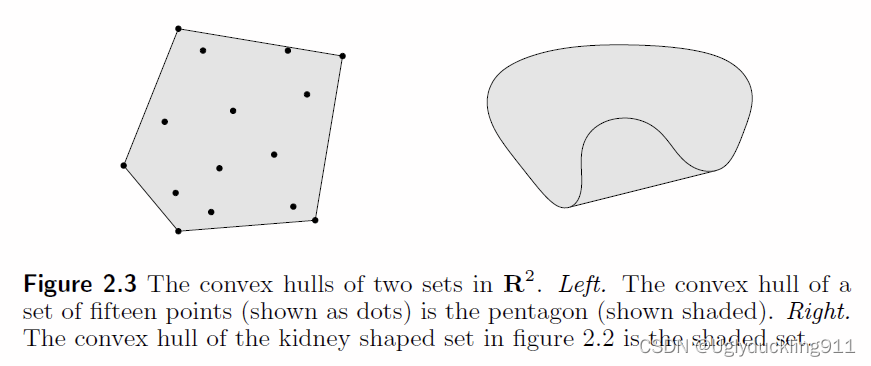
凸包 Convex Hull

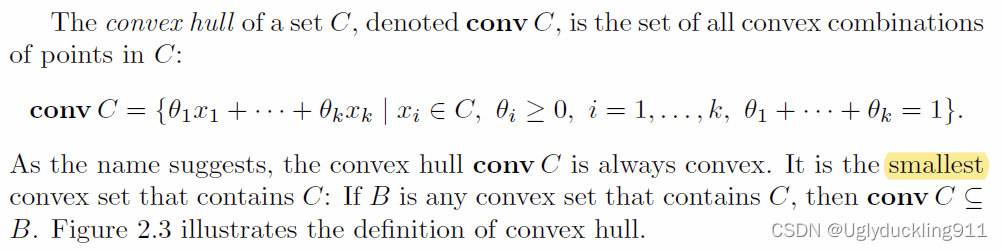
书里面，在对凸包定义的时候，看似没有对$\theta$上限进行范围限制；不过在根据二维定义或者多维中的所有$\theta$之和为1，可以推算出来$\theta$限制在0~1之间。
以下是针对一个集合，所构建的凸包

锥 Cone

C是锥的定义
$$\forall X\in C,\theta \ge 0,有\theta X\in C$$
C是凸锥的定义
$$\forall X_1,X_2\in C,{\theta }_1,{\theta }_2\ge 0,有{\theta }_1{X}_1+{\theta }_2{X}_2\in C$$

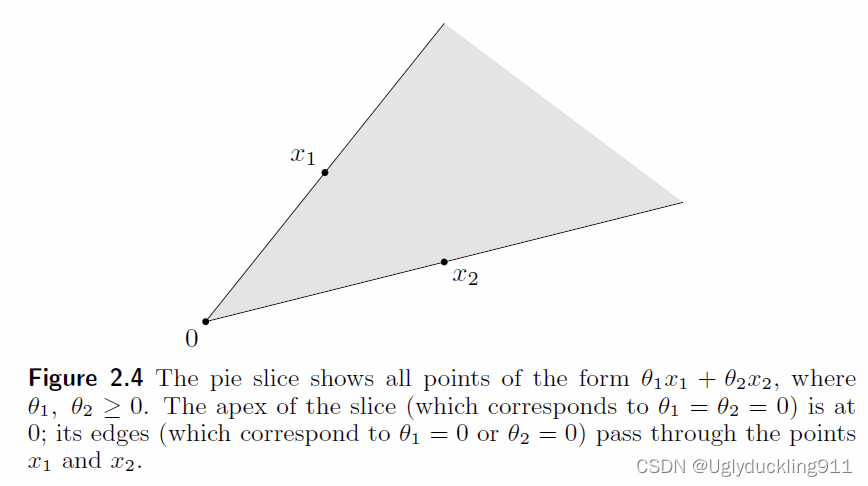
凸锥包

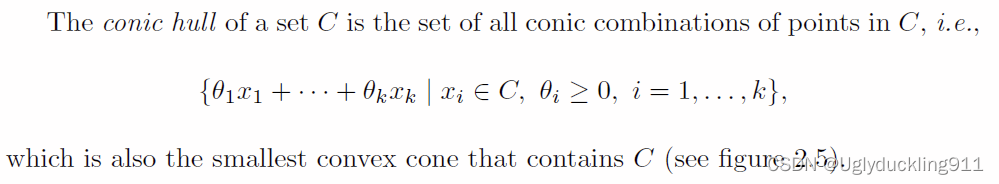
以下是针对一个集合，所构建的凸锥包

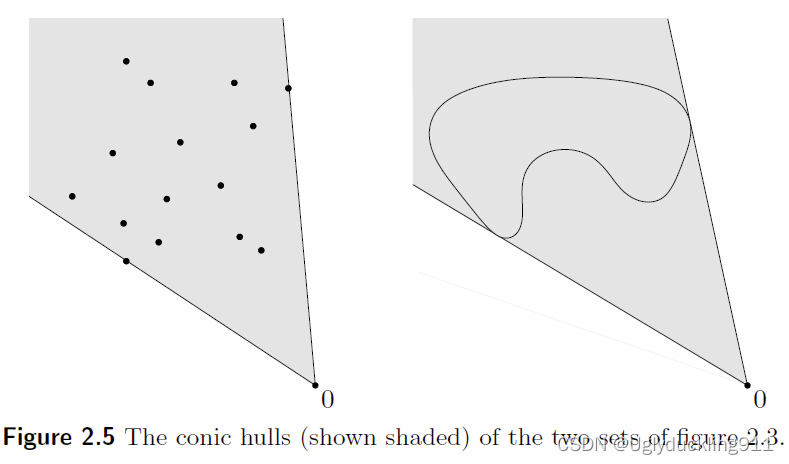
总结

以上主要是对仿射集、凸集、凸锥等概念及其广义化性质进行展示，并且通过几个典型的例子加以说明三者的区别。