4、不仅仅应用于标定的非线性优化问题

一、非线性优化算法通用流程

非线性优化的基本流程可以总结如下(最小化问题)：

可以看到，我们主要的工作就是寻找那个$\Delta x_i$，而不同的寻找方法和更新流程，就对应不同的优化方法。

二、不同的优化方法

1.梯度下降法

上图表示我们目标函数的二维表现形式。我们通过非线性优化的方法找到函数的最小值对应的$x_1$和$x_2$。

其中$g(x)$是$F(x)$的一阶导。$\alpha$为我们设定的步长。为了达到使得目标函数值随自变量变化而减少的要求，得出下降方向$h$。
也就是说，我们在$x$点给定一个步长$\alpha$和一个与一阶导方向夹角大于90°的一个方向$h$,则可以保证目标函数值是向减少的方向更新自变量参数的。

2.最速下降法

最速下降法也很简单，顾名思义就是找到使得目标函数变化率最大的那个方向即可。

即，当函数梯度和下降方向夹角为$\pi$时，迭代更新最快可以达到最小值。

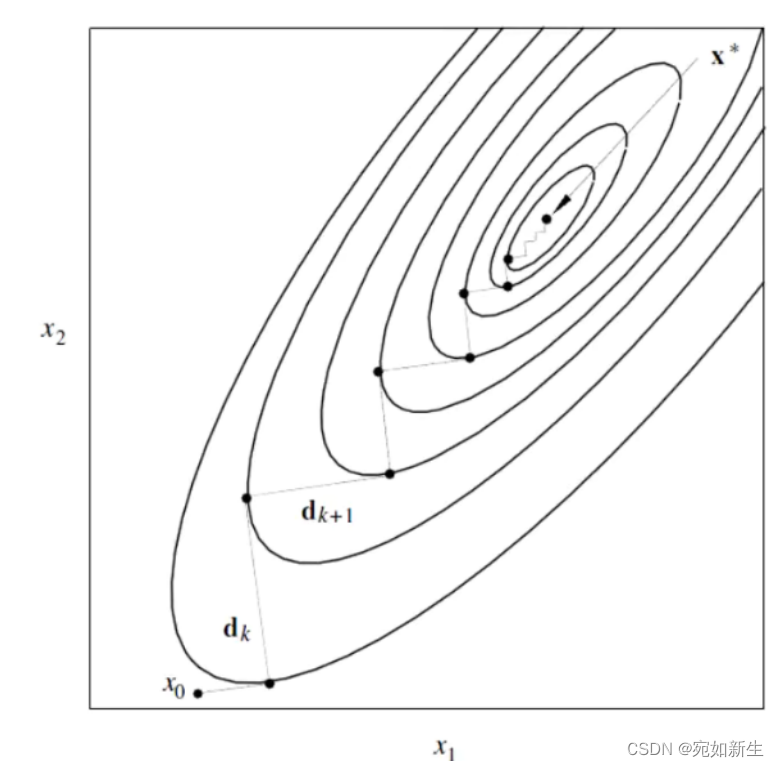
他是有明显缺点的。由于这里面我们要给定他一个非负步长$\alpha$,从上图来看，步长给大了，对后面迭代过程是不友好的，很容易陷入反复，陷入一个死循环。步长给小了效率太低，所以这个$\alpha$很难去合理确定。

3.牛顿法

牛顿法是对最速下降法的一个改进。

我们通过上面的方法就能直接解出$h$，但这也是有条件的，那就是$H$必须正定，但在实际的工程问题中这很难一直保证。
一般情况下，牛顿法中$\alpha =1$。

牛顿法之所以比最速下降法要好就是因为，牛顿法用了泰勒公式进行了二阶近似。求解出来的$h$受二阶导的影响，接近最小值附近时，$h
$会变得更小来适应最后阶段的迭代。
缺点也很明显，他要计算二阶海森矩阵，这是非常复杂的，加大了计算量。

4.高斯-牛顿法

高斯牛顿法又是对牛顿法的改进。

与牛顿法对比，发现高斯牛顿法不是对目标函数进行展开，而是对里面的误差函数$f(x)$进行一阶泰勒展开。代入目标函数，发现得到$J^{T}Jh=-J^{T}f(x)$,与牛顿法的正规方程形式一致，相当于高斯牛顿法用$J^{T}J$近似了牛顿法中很难计算的$H$。这大大降低了牛顿法的计算量。

---

缺点就是，实际工程中我们仍不能一直保证$J^{T}J$是正定的。而且步长取得不能太大，因为一阶泰勒近似在$x$附近才能有很好的近似。

5.LM法

LM法正是解决了上面高斯牛顿法无法保证“海森矩阵”为正定以及步长不能太大的缺点。


可见，LM法既避免了计算复杂的海森矩阵，又保证了信息矩阵的正定性，同时还合理的选择了更新步长。无疑，是这几个优化方法中最好的优化算法。

4、非常感谢您的阅读。