机器人逆运动学（迭代法雅可比矩阵）

1引言

机器人逆运动学（Inverse Kinematics，IK）是机器人学和计算机图形学中的一项重要技术，主要用于求解机器人末端执行器（如机械手或者机器人手臂）在三维空间中达到特定位置和姿态所需的各个关节角度。逆运动学的任务是给定机器人末端执行器的目标位置和姿态，计算出满足这一要求的关节角度。它与正运动学相对，正运动学是通过已知的关节参数计算末端执行器的位置和姿态。机器人逆运动学是研究如何根据已知的末端状态（如末端位置和姿态）推算出控制机器人的关节指令的一门技术。它与正运动学相反，正运动学则是通过传感器数据计算机器人末端的位置和动作，而逆运动学则是从末端状态倒推回关节的控制指令。

2.逆运动学问题

给定的末端执行器位姿求解相应的关节变量成为逆运动学问题。由于机械臂工作时的运动轨迹通常在笛卡尔儿空间规划，而实际可控制的变量是各个关节的量，因此逆运动学问题更令人感兴趣。

3.逆运动学方法及其优缺点 

1. 几何法（Geometric Methods）：

   • 工作原理：利用机械结构的几何特性，将问题转化为向量和矩阵运算，通过逆矩阵（inverse kinematics）计算关节位置。
   • 优点：计算相对简单，适合实时控制，适用于刚性机械结构。
   • 缺点：在处理缓冲区或柔性部件时表现有限，随着关节数量增加，计算效率降低。

2. 优化法（Optimization Methods）：

   • 工作原理：将逆运动学问题转化为优化问题，通过迭代算法（如梯度下降、牛顿拉夫森方法）寻找最优解。
   • 优点：能够处理复杂的非线性约束，适合多关节机器人，支持实时调整控制指令。
   • 缺点：计算资源需求高，可能导致延迟，传感器噪声和环境动态性质会影响优化结果。

3. 参考帧法（Reference Frame Methods）：

   • 工作原理：将末端位置分解为相对于某个参考帧的位姿和局部坐标，简化了状态表示。
   • 优点：简化了复杂机械结构中的关节状态表示，适用于需要动态参考系变换的情况。
   • 缺点：在处理环境动态性质或高度约束时表现有限，计算过程过于依赖具体实现方式。

4. 基于动态规划的方法（Dynamic Programming Methods）：

   • 工作原理：将整个状态空间分解为多个子问题，通过分解和迭代逐步求解。
   • 优点：能够有效解决动态环境中的障碍物避让问题，提高了算法的鲁棒性和适应性。
   • 缺点：计算复杂度较高，可能导致性能下降，需要多次迭代来达到收敛。

5. 混合方法（Mixed Methods）：

   • 优点：综合利用各方法的优势，提升整体性能，适用于复杂且多样化的逆运动学问题。
   • 缺点：实现复杂度较高，需要对多种方法有深入理解，可能导致算法运行时间增加。

6. 基于深度学习的方法（Deep Learning Methods）：

   • 工作原理：利用神经网络映射传感器数据到关节控制指令，通过大量数据训练自动学习复杂环境中的状态转换。
   • 优点：能够捕捉机器人动作中复杂的非线性关系，易于扩展和适应不同机械结构。
   • 缺点：需要大量标注数据支持，数据收集可能耗时且成本高昂，计算资源需求较大，影响实时性。

7. 迭代法（Iteration Methods）：

   • 工作原理：通过迭代更新变量值，逐步逼近解。雅可比矩阵在优化算法中起到关键作用，用来评估目标函数对变量的敏感性。
   • 优点：支持实时调整和缓解非线性约束问题。
   • 缺点：可能导致收敛速度较慢，需要合适的初始值。

8. 雅可比矩阵（Jacobian Matrix）：

   • 作用：在逆运动学优化中，雅可比矩阵用于描述变量之间的关系，并帮助算法选择搜索方向，以更有效地逼近解。
   • 应用场景：广泛应用于梯度下降等优化算法中，特别是在处理复杂约束和多目标优化时。

4.雅可比矩阵 

在进行迭代解之前，要先具备雅可比矩阵的基础知识以及推导过程。

5.matlab代码及实验 

设定的期望位置：
迭代式在第9次迭代收敛到允许误差范围内！
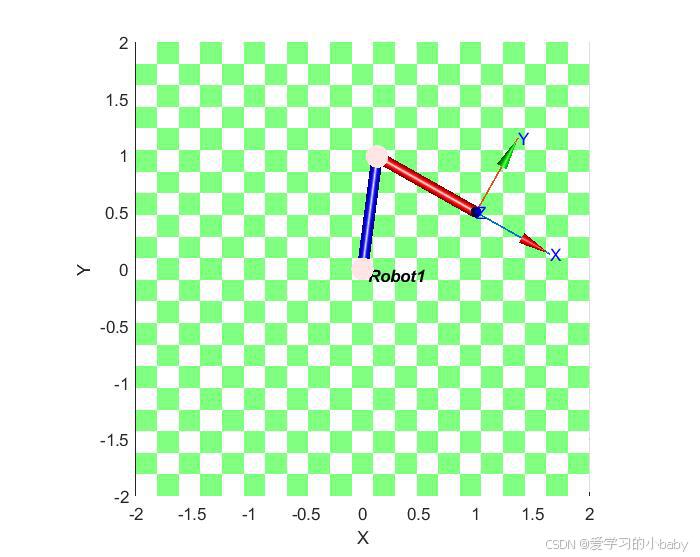
迭代法得到的关节角度为：theta1=82.5772,theta2=-112.0243
迭代式在第10次迭代收敛到允许误差范围内！
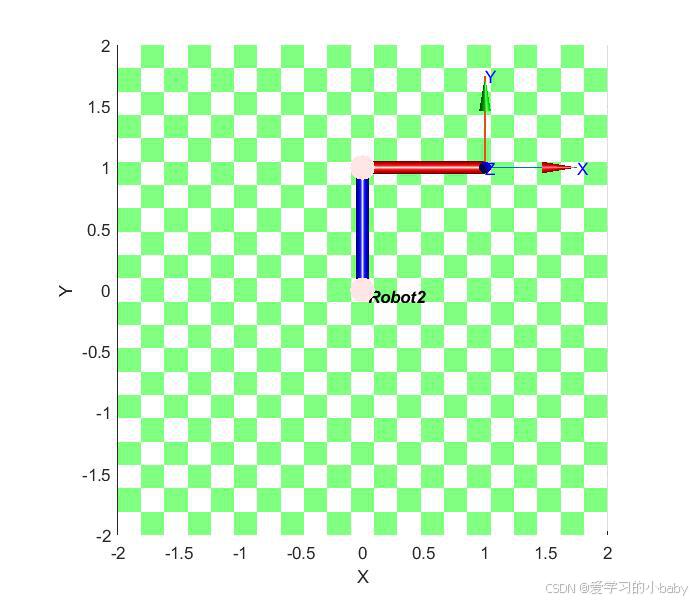
迭代法得到的关节角度为：theta1=90,theta2=-90
 
robot1 = 
 
Robot1 (2 axis, RR, stdDH, fastRNE)                              
                                                                 
+---+-----------+-----------+-----------+-----------+-----------+
| j |     theta |         d |         a |     alpha |    offset |
+---+-----------+-----------+-----------+-----------+-----------+
|  1|         q1|          0|          1|          0|          0|
|  2|         q2|          0|          1|          0|          0|
+---+-----------+-----------+-----------+-----------+-----------+
                                                                 
grav =    0  base = 1  0  0  0   tool =  1  0  0  0              
          0         0  1  0  0           0  1  0  0              
       9.81         0  0  1  0           0  0  1  0              
                    0  0  0  1           0  0  0  1              
 
期望末端位置：xd=1,yd=0.5我计算出的实际末端位置：x=1,yd=0.5
 
robot2 = 
 
Robot2 (2 axis, RR, stdDH, fastRNE)                              
                                                                 
+---+-----------+-----------+-----------+-----------+-----------+
| j |     theta |         d |         a |     alpha |    offset |
+---+-----------+-----------+-----------+-----------+-----------+
|  1|         q1|          0|          1|          0|          0|
|  2|         q2|          0|          1|          0|          0|
+---+-----------+-----------+-----------+-----------+-----------+
                                                                 
grav =    0  base = 1  0  0  0   tool =  1  0  0  0              
          0         0  1  0  0           0  1  0  0              
       9.81         0  0  1  0           0  0  1  0              
                    0  0  0  1           0  0  0  1              
 
期望末端位置：xd=1,yd=1我计算出的实际末端位置：x=1,yd=1

clc;clear;close all;
%步骤一 计算利用雅可比矩阵的迭代解
L1=1;%第一个连杆长度
L2=1;%第二个连杆长度
theta0=[0;0];%机器人的初始关节角度
%设定最大接待次数
max_iterations=100;
%设定容许误差
tolerance=1e-6;%判断迭代是否收敛即当前计算结果与目标位置之间的差距是否足够小
disp('设定的期望位置：');
xd1=1;
yd1=0.5;
%计算逆解
[theta1,converged1]=inverse_kinematics(xd1,yd1,L1,L2,theta0, ...
    max_iterations,tolerance);%converged1: 输出的布尔值指示算法是否成功收敛
if converged1
    disp(['迭代法得到的关节角度为：theta1=',num2str(theta1(1)*180/pi), ...
        ',theta2=',num2str(theta1(2)*180/pi)]);
else
    disp('迭代失败');
end
xd2=1;
yd2=1;
%计算逆解
[theta2,converged2]=inverse_kinematics(xd2,yd2,L1,L2,theta0, ...
    max_iterations,tolerance);
if converged2
    disp(['迭代法得到的关节角度为：theta1=',num2str(theta2(1)*180/pi), ...
        ',theta2=',num2str(theta2(2)*180/pi)]);
else
    disp('迭代失败');
end
%步骤二 利用机器人工具箱验证
%定义机械臂模型
%% 
figure;
L1=Link('d',0,'a',1,'alpha',0);%第一段连杆
L2=Link('d',0,'a',1,'alpha',0);%第二段连杆
robot1=SerialLink([L1 L2],'name','Robot1');
robot1.display();
q1=[theta1(1) theta1(2)];% 将逆运动学计算出的关节角度赋值给 q1
robot1.plot(q1)% 绘制机械臂在给定关节角度下的姿态
T=robot1.fkine(q1);
pos=T(1:3,4);
%关节角对应的末端位置 （与期望末端位置对比）
x=pos(1);
y=pos(2);
disp(['期望末端位置：xd=',num2str(xd1),',yd=',num2str(yd1), ...
    '我计算出的实际末端位置：x=',num2str(x),',yd=',num2str(y)]);
figure;%创建一个新的图形窗口
L1=Link('d',0,'a',1,'alpha',0);%第一段连杆
L2=Link('d',0,'a',1,'alpha',0);%第二段连杆
robot2=SerialLink([L1 L2],'name','Robot2');%创建一个串联机械臂模型
robot2.display();% 显示机械臂的结构
q2=[theta2(1) theta2(2)];
robot2.plot(q2)
T=robot2.fkine(q2);% 计算正向运动学，得到末端执行器的转换矩阵
pos=T(1:3,4);% 从转换矩阵中提取末端位置（x, y, z）
%关节角对应的末端位置 （与期望末端位置对比）
x=pos(1);
y=pos(2);
disp(['期望末端位置：xd=',num2str(xd2),',yd=',num2str(yd2), ...
    '我计算出的实际末端位置：x=',num2str(x),',yd=',num2str(y)]);
%二连杆机械臂逆运动学求解函数
function[theta,converged]=inverse_kinematics(xd,yd,L1,L2,theta0, ...
    max_itertions,tolerance)
%xd,yd:目标坐标
%L1,L2:两个连杆长度
%theta0：初始关节角度
%max_iterations:最大迭代次数
%tolerance:目标误差
%theta：求解得到的关节角度
%converged：是否收敛
    theta=theta0;% 初始化当前关节角度
    converged=false;% 初始化收敛状态为false
    for i=1:max_itertions
    %计算雅可比矩阵
      J=[-L1*sin(theta(1))-L2*sin(theta(1)+theta(2)),-L2*sin(theta(1)+theta(2));
          L1*cos(theta(1))+L2*cos(theta(1)+theta(2)),L2*cos(theta(1)+theta(2))];
        %计算当前末端坐标
        x=L1*cos(theta(1))+L2*cos(sum(theta));
        y=L1*sin(theta(1))+L2*sin(sum(theta));
        %计算期望末端位置与当前末端位置的误差
        e=[xd-x;yd-y];
        %判断误差是否满足要求
        %e 是一个向量时norm(e) 计算的是该向量的 L2 范数（也称为欧几里得范数)
        %norm(e) 被用来计算期望末端位置与当前末端位置之间的误差大小
        if norm(e)<tolerance
            converged=true;
            disp(['迭代式在第',num2str(i),'次迭代收敛到允许误差范围内！']);
            break;
        end
        %利用迭代式更新关节角度（由于雅可比矩阵）
        %如果雅可比矩阵
        [m,n]=size(J);
        if m==n&&det(J)~=0  %如果雅可比矩阵是方阵且行列式不等于0（秩为2），
                            %则迭代式直接使用雅可比矩阵的逆
            theta=theta+inv(J)*e;%inv(J) 计算雅可比矩阵的逆矩阵，
            % 乘以误差 (e) 后，可以得到需要调整的关节角度，
            % 直接加到当前的关节角度 (\theta) 上
        else%否则迭代式使用雅可比矩阵的伪逆
            theta=theta+pinv(J)*e;%这是一种扩展的逆运算
            % 适用于非方阵或奇异矩阵
        end
    end
        %将最终的迭代角度映射到-pi~pi
        %wrapToPi180(angle)形参是角度,作用是将角度映射为-180~180
        theta=wrapToPi(theta);
        if ~converged
            warning('迭代未收敛！');
        end
    
end
% function[theta,converged] = inverse_kinematics(xd,yd,L1,L2,theta0,max_iterations,tolerance)
% theta = theta0;
% converged = false;
% for i = 1:max_iterations
% J=[-L1*sin(theta(1))-L2*sin(theta(1)+theta(2)),-L2*sin(theta(1)+theta(2));L1*cos(theta(1))+L2*cos(theta(1)+theta(2)),L2*cos(theta(1)+theta(2))];
% x=L1*cos(theta(1))+L2*cos(sum(theta));
% y=L1*sin(theta(1))+L2*sin(sum(theta));
% e=[xd - x;yd - y];
% if norm(e)<tolerance
% converged=true;
% disp(['迭代式在第',num2str(i),'次迭代收敛到允许误差范围内！']);
% break;
% end
% [m,n]=size(J);
% if m==n&&det(J)~=0
% theta=theta + inv(J)*e;
% else
% theta = theta + pinv(J)*e;
% end
% end
% theta=wrapToPi(theta);%warpTo180(angle)形参是角度，作用是将角度映射为-180°~180°
% if ~converged
% warning('迭代未收敛！');
% end
% end