【发作期行波估计的多变量线性回归】测试癫痫样放电是否组织为行波，并推断其速度（Matlab代码实现）-CSDN博客

本文链接：https://blog.csdn.net/Yan_she_He/article/details/144415121

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

⛳️赠与读者

💥1 概述

一、引言

二、研究背景

三、研究方法

四、实验设计与结果分析

五、讨论与展望

六、结论

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码实现

⛳️赠与读者

👨‍💻做科研，涉及到一个深在的思想系统，需要科研者逻辑缜密，踏实认真，但是不能只是努力，很多时候借力比努力更重要，然后还要有仰望星空的创新点和启发点。建议粉丝按目录次序逐一浏览，免得骤然跌入幽暗的迷宫找不到来时的路，它不足为你揭示全部问题的答案，但若能让人胸中升起一朵朵疑云，也未尝不会酿成晚霞斑斓的别一番景致，万一它给你带来了一场精神世界的苦雨，那就借机洗刷一下原来存放在那儿的“躺平”上的尘埃吧。

或许，雨过云收，神驰的天地更清朗.......🔎🔎🔎

💥1 概述

【发作期行波估计的多变量线性回归】测试癫痫样放电是否组织为行波，并推断其速度研究文档

我提供了几种回归方法来估计高分辨率脑电图数据中的行波速度。你可以通过观察多单位尖峰或局部场电位的时空分布，然后估计它们的速度，来统计性地测试行波的存在。点过程、包络（时间序列）和互相关方法都提供了鲁棒选项（最小绝对偏差法）

一、引言

癫痫是一种慢性神经系统疾病，其发作时的大脑电活动异常复杂。研究癫痫样放电的时空分布特性，特别是是否组织为行波，对于理解癫痫的发病机制及指导治疗具有重要意义。本文旨在探讨利用多变量线性回归方法估计高分辨率脑电图（EEG）数据中的行波速度，以统计性地测试行波的存在并推断其速度。

二、研究背景

癫痫与脑电图：
- 脑电图是记录大脑电活动的非侵入性技术，对于癫痫的诊断和治疗具有重要意义。
- 癫痫发作时的脑电信号与正常状态下相比有明显的差异，表现为不规则、程度各异的痫样放电。
行波与癫痫样放电：
- 行波是指在空间上连续传播的电信号波。
- 在癫痫研究中，行波的存在与否及其速度对于理解癫痫样放电的传播机制至关重要。

三、研究方法

数据预处理：
- 对高分辨率脑电图数据进行滤波、去噪和伪迹处理，以确保信号的纯净性和可靠性。
特征提取：
- 从预处理后的EEG信号中提取有用的信息，如时域特征、频域特征和时频域特征。
- 特别是要提取与行波相关的特征，如波形的时空分布、传播方向等。
多变量线性回归：
- 构建多变量线性回归模型，以时空分布为自变量，行波速度为因变量。
- 利用回归模型估计行波速度，并统计性地测试行波的存在。
其他方法比较：
- 将多变量线性回归方法与点过程、包络（时间序列）和互相关等方法进行比较，以评估其性能和鲁棒性。

四、实验设计与结果分析

实验设计：
- 选择一定数量的癫痫患者作为研究对象，记录其发作期的脑电图数据。
- 对数据进行预处理和特征提取后，应用多变量线性回归方法估计行波速度。
结果分析：
- 观察回归模型的拟合效果，评估行波速度的估计准确性。
- 比较不同方法下的行波速度估计结果，分析多变量线性回归方法的优势和局限性。
- 统计性地测试行波的存在，并探讨其可能的生理机制。

五、讨论与展望

讨论：
- 分析多变量线性回归方法在估计行波速度中的优势和不足。
- 探讨其他可能影响行波速度的因素，如癫痫类型、病灶位置等。
展望：
- 进一步优化多变量线性回归模型，提高行波速度的估计准确性。
- 探索其他先进的信号处理技术，以更全面地理解癫痫样放电的时空分布特性。
- 将研究结果应用于癫痫的临床诊断和治疗中，为改善患者的生活质量提供科学依据。

六、结论

本文利用多变量线性回归方法估计了高分辨率脑电图数据中的行波速度，并统计性地测试了行波的存在。实验结果表明，多变量线性回归方法能够有效地估计行波速度，为理解癫痫样放电的传播机制提供了新的视角。然而，该方法仍存在一些局限性，需要进一步优化和完善。未来的研究将致力于探索更先进的信号处理技术和更全面的实验设计，以更深入地理解癫痫的发病机制并指导治疗。

📚2 运行结果

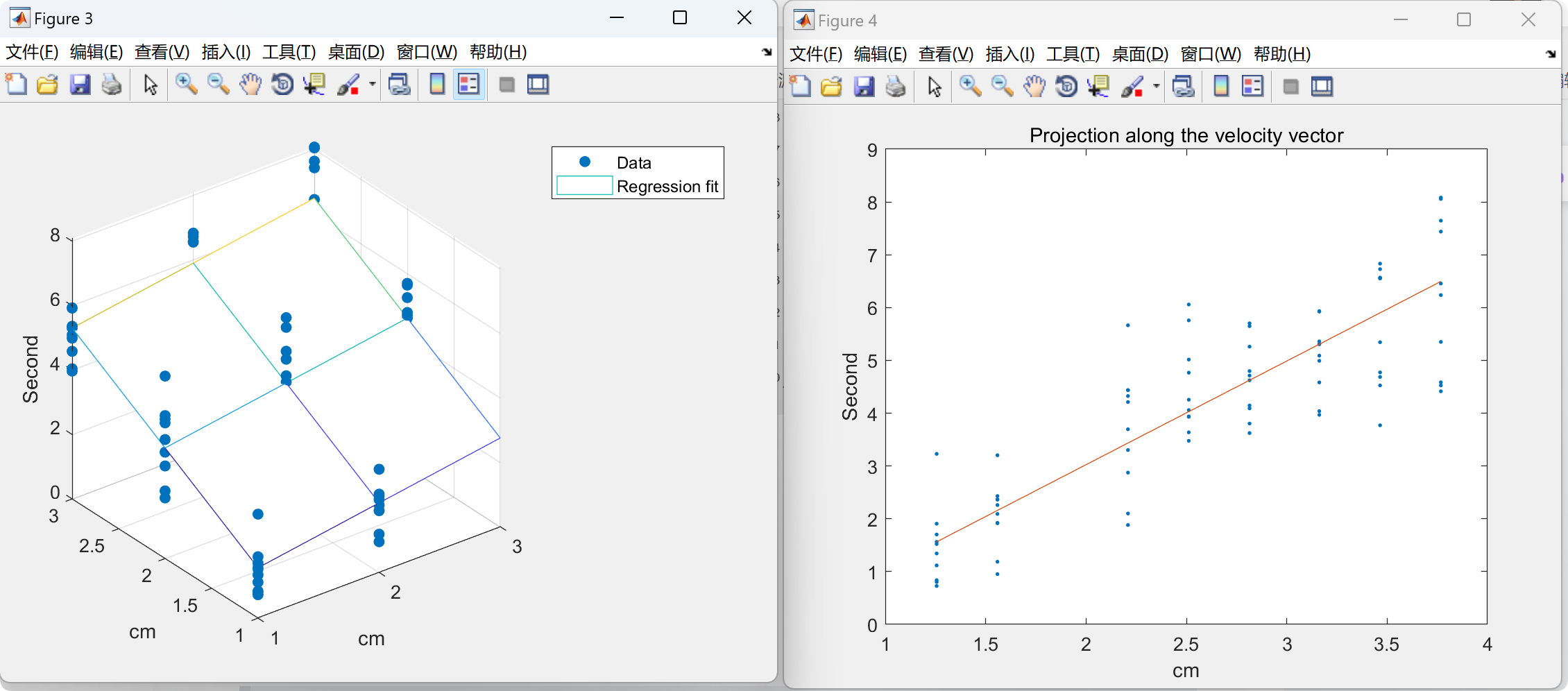
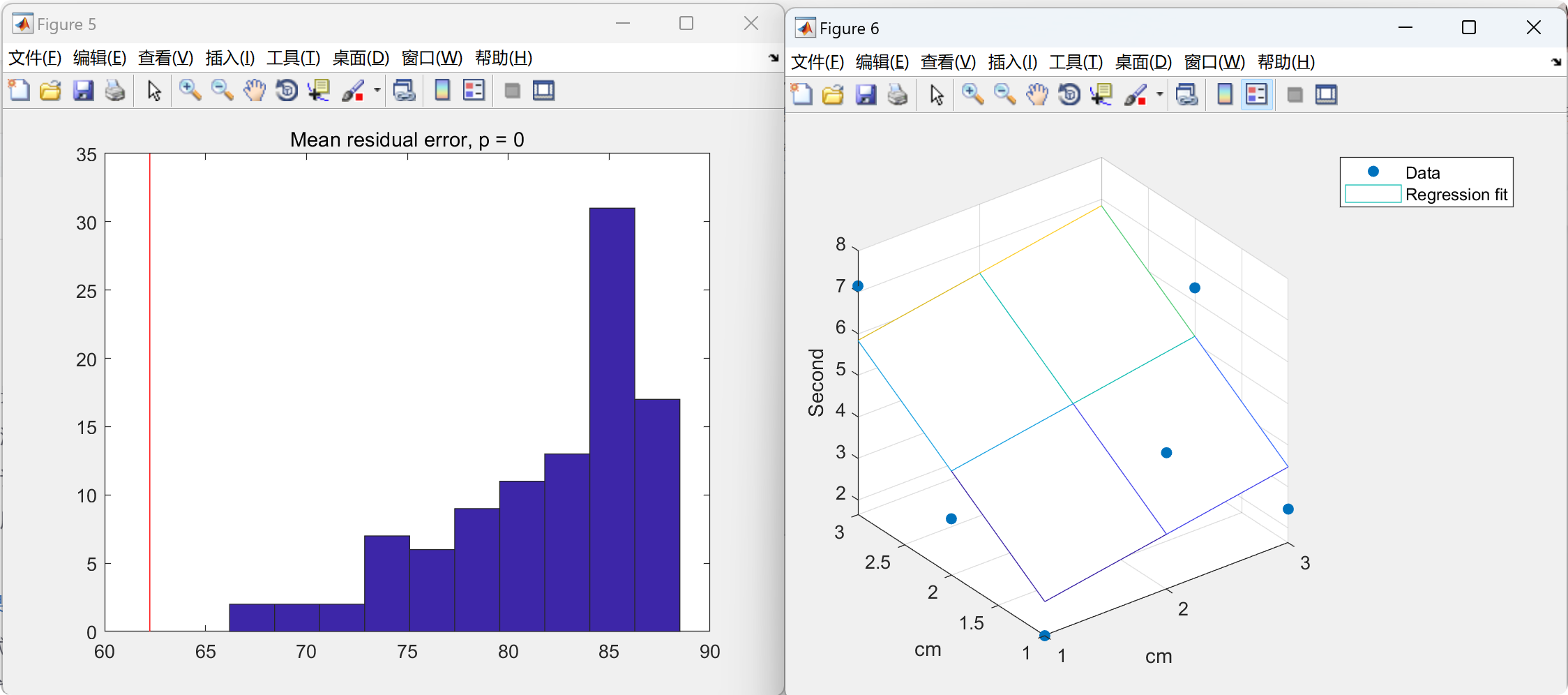
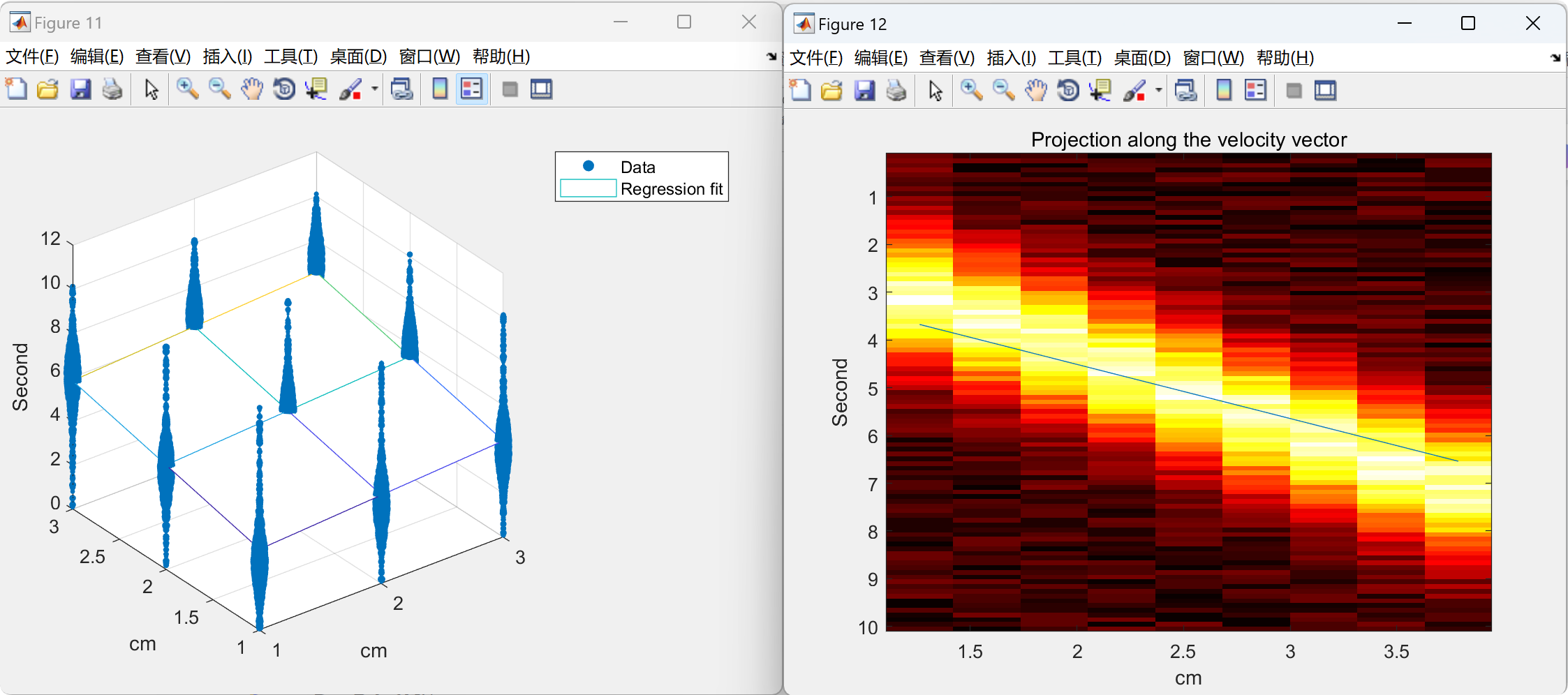
部分代码：

% Multiunit estimator
Beta = [0.5;1.5]; % this is the ground truth for beta
T = P * Beta;
T = repmat(T,[1,10]); % Each channel can have several events
T = T + randn(size(T)); % Get some noise
T = mat2cell(T,ones(size(T,1),1),size(T,2)); % Put those spikes in cells
T{7} = []; % For example, channel 7 fails to detect any spike
[beta, V, p] = SpatialLinearRegression(T,P,'switch_plot',1) % Least square estimator
[beta, V, p] = SpatialLinearRegression(T,P,'switch_plot',1,'Lossfun','L1') % Least absolute deviation estimator

%% Negative peak & maximal descent estimator
Beta = [0.5;1.5]; % this is the ground truth for beta
T = P * Beta; % This is the timing of negative peak/maximal descent
T = T + randn(size(T)); % Get some noise
T = mat2cell(T,ones(size(T,1),1),size(T,2)); % Put those spikes in cells
[beta, V, p] = SpatialLinearRegression(T,P,'switch_plot',1) % Least square estimator
[beta, V, p] = SpatialLinearRegression(T,P,'switch_plot',1,'Lossfun','L1') % Least absolute deviation estimator

%% High gamma envelope estimator
Beta = [0.5;1.5]; % this is the ground truth for beta
T = P * Beta; % This is the timing of maximal gamma power
% Suppose gamma power is Gaussian distributed around the gamma power peak
T_grid = mean(T) + (-50:50)/10;% Let's look at 101 data points around the ictal discharge, & suppose sampling rate = 10
W = normpdf(bsxfun(@minus,T_grid,T),0,1);
W = W + rand(size(W))*max(W(:))/5; % Give it some background noise
imagesc(W); % This is gamma power
[beta, V, p] = SpatialLinearRegression(W,P,'switch_plot',1,'Fs',10) % Least square estimator
[beta, V, p] = SpatialLinearRegression(W,P,'switch_plot',1,'Lossfun','L1','Fs',10) % Least absolute deviation estimator