【建模与控制网络物理系统】由7个磁悬浮系统(Maglev)组成的网络物理系统，设计分布式控制协议，多智能体系统执行协同跟踪任务研究（Matlab代码、Simulink仿真实现）-CSDN博客

本文链接：https://blog.csdn.net/Yan_she_He/article/details/145791158

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

⛳️赠与读者

💥1 概述

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码、Simulink仿真、数据、文档讲解下载

⛳️赠与读者

👨‍💻做科研，涉及到一个深在的思想系统，需要科研者逻辑缜密，踏实认真，但是不能只是努力，很多时候借力比努力更重要，然后还要有仰望星空的创新点和启发点。建议读者按目录次序逐一浏览，免得骤然跌入幽暗的迷宫找不到来时的路，它不足为你揭示全部问题的答案，但若能解答你胸中升起的一朵朵疑云，也未尝不会酿成晚霞斑斓的别一番景致，万一它给你带来了一场精神世界的苦雨，那就借机洗刷一下原来存放在那儿的“躺平”上的尘埃吧。

或许，雨过云收，神驰的天地更清朗.......🔎🔎🔎

💥1 概述

建模与控制网络物理系统

1 引言

在本文中，我们研究了一个由7个磁悬浮系统（Maglev）组成的网络物理系统（Cyber-Physical System）。我们设计了一个分布式控制协议，其中多智能体系统执行协同跟踪任务。考虑到不同的网络通信结构，我们比较了这些不同选择对受控系统的影响。随后，我们选择了一个特定的网络结构，以便突出显示在领导者稳态代理参考行为发生变化的不同场景之间的收敛时间点。此外，我们还分析了在输出测量中引入噪声的影响，以及用于设计控制器和观测器的不同变量的影响。

2 通信网络

在实验中，我们尝试了不同的网络结构，从最简单的星型连接结构（每个跟随节点都与领导者相连）到更复杂的结构。我们将深入讨论每种情况。

2.1 星型配置

这是最简单的配置。在这种情况下，所有智能体的收敛时间是相同的，因为它们同时接收到相同的信息，因此不需要等待其他智能体。正如预期的那样，这是性能最好的网络结构，但由于其简单性以及每个跟随者的动态特性相同，使得第一个跟随者与其他跟随者无法区分，因此我们决定不在接下来的实验部分中选择它。

2.2 分支配置

在分支版本中，我们创建了两个跟随节点的分支，每个分支的头部都连接到领导者节点。每个分支由3个跟随者组成（分别标记为偶数分支和奇数分支），其中每个节点的行为与其在另一个分支中对应的平行节点相同（1-2，3-4，5-6）。我们尝试通过添加边（例如从6到1）来修改这种结构，并随后改变其权重；这两种变化分别可以在图（3）中看到。前者展示了添加这条边如何将奇数分支向偶数分支的最后一个智能体靠拢，而后者则进一步增加了这种偏移，体现在动态行为中。

2.3 队列配置

在队列版本中，正如其名称所示，每个跟随节点从领导者节点开始依次连接到下一个节点。我们将这种结构称为标准队列。我们测试了一些变化，例如从6到1的边，以及从6到2的边，并分别使用原始权重和修改后的权重；以下图表展示了这些不同配置的动态行为。与分支结构类似，从6到1的边使所有智能体向最后一个智能体靠拢，而从6到2的边则保持第一个智能体的行为不变。在标准队列中，收敛时间明显低于其他两种结构，这是由于耦合增益比其他两种配置要高得多。

详细文档讲解见底第4部分。

📚2 运行结果

剩下的去掉图框：

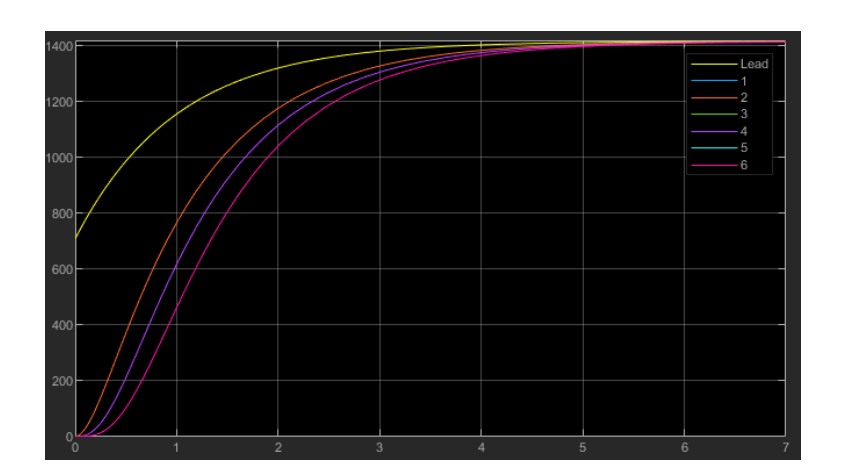
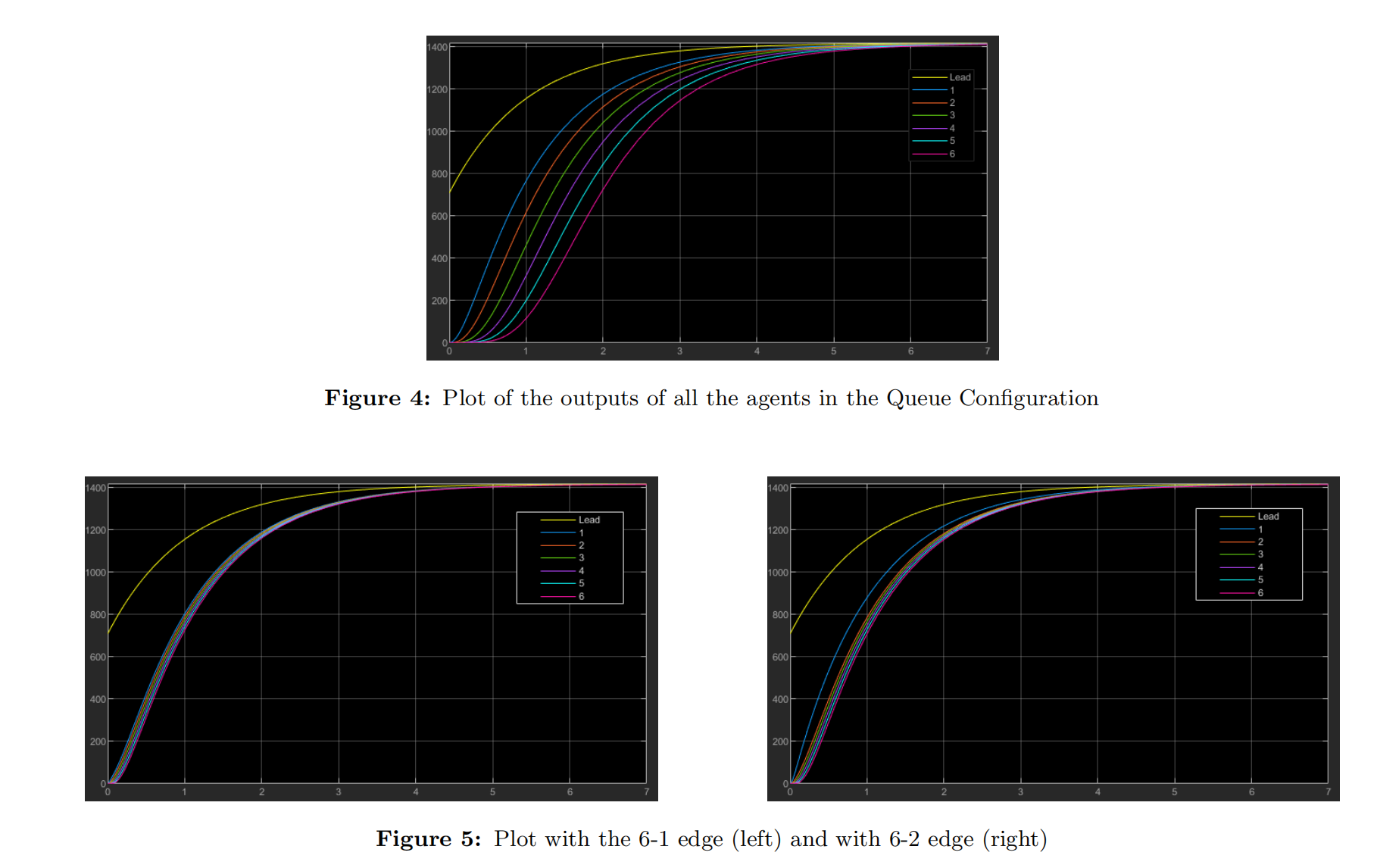
Simulink版本：2020a，低版本可能会报错。

部分代码：

%Initial conditions
random = 1;
if (random == 1)
x0 = [((rand(1,6)*4)-1)/C(1,1);rand(1,6)/707.27]; %agent
else
x0 = [0,0];
end

x1 = [0;1/707.27]; %leader

%Poles for steady-state reference
pconst = [0 -1];
psine = [-j +j];
pramp = [0 0];
p = psine;
%%Parameter GRID-SEARCH
%use cellcomb as combination of values
% cmul = [1 2 5 10 15 20 25 30 35 40 45 50 55 60 65 70 75 80 85 90 95 100];
% Rval = [0.1 1 2 10 50 100];
% Qval = [0.1 1 2 10 50 100];
% val = {cmul,Rval,Qval};
% cellcomb = cell(1,numel(val));
% [cellcomb{:}] = ndgrid(val{:});
% cellcomb = cellfun(@(X) reshape(X,[],1),cellcomb,'UniformOutput',false);
% cellcomb = horzcat(cellcomb{:})
cellcomb = 1;
%%NETWORK STRUCTURES
% LINE STRUCTURE
Adj = tril(ones(6),-1) - tril(ones(6),-2);
Deg = diag(sum(Adj,2));
Pinning = zeros(6);
Pinning(1,1) = 1;
L = Deg- Adj;
c = 1/(2*min(real(eig(L+Pinning))));

%% Local Agent state dynamics control
Kctrl = acker(A,B,[p]);
A = A-B*Kctrl;

%Information gathering
umax = zeros(6,length(cellcomb));
ut0 = zeros(6,length(cellcomb));
d = zeros(2,length(cellcomb));
umaxn = zeros(6,length(cellcomb));
ut0n = zeros(6,length(cellcomb));
dn = zeros(2,length(cellcomb));
ctemp = c;

w=warning('off','all');
for i=1:length(cellcomb)
%Q R and c gridsearch
% c = ctemp*cellcomb(i,1);
% Q = eye(2)*cellcomb(i,2);
% R = cellcomb(i,3);
%Choose Q and R and cfrom test
Q = eye(2)*50;
R = 10;
c = ctemp*10;

%SVFB
%%Feedback GAIN control matrix K
Pk = are(A,B*inv(R)*B',Q);
K = inv(R)*B'*Pk;

%% Observer gain Fn/Fl
Pn = are(A',C'*inv(R)*C,Q);
% Fn = Pneigh*C'*inv(R);
Fn = Pn*C'*inv(R);
%Local f
Fl = -Fn;

%Hurwitz check, if
if(Hurwitz(A,c,L,Pinning,Fn,C) == 0)
disp("\t Variables were non Hurwitz\n")
disp("Variable c:\n")
disp(c)
disp("Variable R:\n")
disp(R)
disp("Variable Q:\n")
disp(Q)
continue;
end
simOut = sim('neighbour_generalized');
%%LOCAL INFOGATHER
%Get time at with input is 0 for each agent
ut0(1,i) = simOut.get('u1').time(find( abs(simOut.get('u1').data) >= -1e-3 ,1,'last'));
ut0(2,i) = simOut.get('u2').time(find( abs(simOut.get('u2').data) >= -1e-3 ,1,'last'));
ut0(3,i) = simOut.get('u3').time(find( abs(simOut.get('u3').data) >= -1e-3 ,1,'last'));
ut0(4,i) = simOut.get('u4').time(find( abs(simOut.get('u4').data) >= -1e-3 ,1,'last'));
ut0(5,i) = simOut.get('u5').time(find( abs(simOut.get('u5').data) >= -1e-3 ,1,'last'));
ut0(6,i) = simOut.get('u6').time(find( abs(simOut.get('u6').data) >= -1e-3 ,1,'last'));

%Max input for each agent
umax(1,i) = max(abs(simOut.get('u1').data));
umax(2,i) = max(abs(simOut.get('u2').data));
umax(3,i) = max(abs(simOut.get('u3').data));
umax(4,i) = max(abs(simOut.get('u4').data));
umax(5,i) = max(abs(simOut.get('u5').data));
umax(6,i) = max(abs(simOut.get('u6').data));

%Delta is global disagreement
delta6x1 = simOut.get('delta6x1').data;
delta6x2 = simOut.get('delta6x2').data;

delta6t = simOut.get('delta6x1').time;
%Find convergence time for each experiment
d(1,i) = delta6t( find( abs(delta6x1) >= 1e-3 ,1,'last'));
d(2,i) = delta6t( find( abs(delta6x2) >= 1e-3 ,1,'last'));

%%NEIGHBOURHOOD INFOGATHER
ut0n(1,i) = simOut.get('un1').time(find( abs(simOut.get('un1').data) >= -1e-3 ,1,'last'));
ut0n(2,i) = simOut.get('un2').time(find( abs(simOut.get('un2').data) >= -1e-3 ,1,'last'));
ut0n(3,i) = simOut.get('un3').time(find( abs(simOut.get('un3').data) >= -1e-3 ,1,'last'));
ut0n(4,i) = simOut.get('un4').time(find( abs(simOut.get('un4').data) >= -1e-3 ,1,'last'));
ut0n(5,i) = simOut.get('un5').time(find( abs(simOut.get('un5').data) >= -1e-3 ,1,'last'));
ut0n(6,i) = simOut.get('un6').time(find( abs(simOut.get('un6').data) >= -1e-3 ,1,'last'));


umaxn(1,i) = max(abs(simOut.get('un1').data));
umaxn(2,i) = max(abs(simOut.get('un2').data));
umaxn(3,i) = max(abs(simOut.get('un3').data));
umaxn(4,i) = max(abs(simOut.get('un4').data));
umaxn(5,i) = max(abs(simOut.get('un5').data));
umaxn(6,i) = max(abs(simOut.get('un6').data));