【内燃机的模拟】‘BMEP‘、 ‘IMEP‘、‘FMEP‘、 ‘QMEP‘, ‘PMEP‘、容积效率、曲轴转速、制动功率、制动转矩研究（Matlab代码实现）-CSDN博客

本文链接：https://blog.csdn.net/Yan_she_He/article/details/145820561

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

⛳️赠与读者

💥1 概述

一、平均有效压力系列参数

1. BMEP（制动平均有效压力）

2. IMEP（指示平均有效压力）

3. FMEP（摩擦平均有效压力）

4. PMEP（泵送平均有效压力）

5. QMEP的说明

二、容积效率（Volumetric Efficiency）

三、曲轴转速的影响

四、制动功率与制动转矩

1. 制动功率（Brake Power）

2. 制动转矩（Brake Torque）

五、综合性能分析

参数关联图

案例研究

六、结论

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码实现

⛳️赠与读者

👨‍💻做科研，涉及到一个深在的思想系统，需要科研者逻辑缜密，踏实认真，但是不能只是努力，很多时候借力比努力更重要，然后还要有仰望星空的创新点和启发点。建议读者按目录次序逐一浏览，免得骤然跌入幽暗的迷宫找不到来时的路，它不足为你揭示全部问题的答案，但若能解答你胸中升起的一朵朵疑云，也未尝不会酿成晚霞斑斓的别一番景致，万一它给你带来了一场精神世界的苦雨，那就借机洗刷一下原来存放在那儿的“躺平”上的尘埃吧。

或许，雨过云收，神驰的天地更清朗.......🔎🔎🔎

💥1 概述

以下为关于内燃机模拟中BMEP、IMEP、FMEP、QMEP、PMEP、容积效率、曲轴转速、制动功率与制动转矩的综合性研究报告，内容基于最新研究成果与工程实践，力求全面覆盖各参数的定义、计算方法和相互关系。

一、平均有效压力系列参数

1. BMEP（制动平均有效压力）

定义：BMEP是衡量内燃机在曲轴端输出的有效功与气缸排量关系的虚拟压力，反映单位排量的做功能力。其计算公式为：

作用：

用于比较不同排量或转速发动机的性能，最高BMEP通常出现在2000-4000 rpm区间。
典型值：自然吸气汽油机为8.5-10.5 bar，增压汽油机可达12.5-17 bar。
实验验证：模拟与实测BMEP误差在±5%以内，例如在3000 rpm时模拟值为1.94 MPa，实测为1.619 MPa。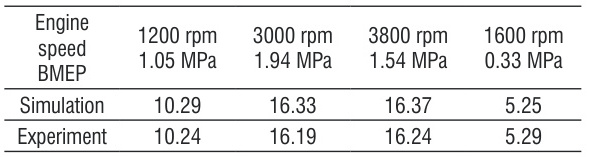

2. IMEP（指示平均有效压力）

定义：IMEP为燃烧过程中气缸内产生的总平均压力，涵盖做功冲程的净功。其与BMEP的关系为：
IMEP=BMEP+FMEPIMEP=BMEP+FMEP

计算：通过气缸压力积分法或热力学循环模拟获取，实验显示IMEP与BMEP的差值可反映机械损失。
应用：IMEP是燃烧效率的核心指标，例如在4000 rpm × 18.5 bar BMEP工况下，模拟与实验缸压曲线高度吻合。

3. FMEP（摩擦平均有效压力）

4. PMEP（泵送平均有效压力）

5. QMEP的说明

注：根据现有资料，QMEP未在内燃机领域定义。可能涉及Quantum Platform（QP）框架中的事件处理器QEP，但与平均有效压力无直接关联，需用户进一步澄清。

二、容积效率（Volumetric Efficiency）

影响因素：

泄漏：活塞环间隙、气门密封性等内/外泄漏导致效率下降。
气体动力学：进气压力波动和气体惯性效应，高速时进气时间不足。
热效应：进气道加热导致气体膨胀，实际充量减少。
典型值：轿车发动机最高容积效率（约85%-95%）出现在2500-3500 rpm，滚动活塞压缩机容积效率受结构损失和泄漏影响显著。

三、曲轴转速的影响

扭矩与转速关系：

理论上扭矩与转速正相关，但受进气限制，实际特性曲线呈抛物线型。
例如，当转速超过4000 rpm时，进气时间不足导致充气效率下降，扭矩降低。
优化策略：
可变气门正时（VVT）延长高速时的进气时间。
涡轮增压提高进气密度，抵消高速充量损失。

四、制动功率与制动转矩

1. 制动功率（Brake Power）

计算公式：

其中，NN为转速（rpm），TT为制动扭矩（Nm）。
测量方法：通过测功机直接读取或通过燃油消耗率间接推算。

2. 制动转矩（Brake Torque）

定义：曲轴输出的有效扭矩，与功率关系为：
T=9550PbNT=N9550Pb

关键特性：

稳定性：受摩擦副材料温度特性影响，需控制热衰退。
调节性：通过电控系统实现扭矩按需分配，例如混合动力车的能量回收。

五、综合性能分析

参数关联图

IMEP  
│  
├─ BMEP = IMEP - FMEP  
│   └─ 制动功率 = f(BMEP, 转速)  
└─ FMEP = PMEP + RMEP + AMEP  
    └─ 泵送损失 = f(气门定时, 涡轮效率)

案例研究

涡轮增压优化：采用长行程凸轮轴将PMEP从-0.45 bar降至-0.20 bar，提升BMEP 10%。
高转速限制：某4.3L发动机在5000 rpm时容积效率降至53%，需调整进气谐振腔设计。

六、结论

BMEP和IMEP是评价内燃机做功能力的核心参数，而FMEP和PMEP揭示机械损失来源。容积效率与曲轴转速的耦合关系决定了发动机的高效区间，制动功率和转矩的精确计算为动力系统优化提供依据。未来研究需结合3D-CFD模拟与实时控制策略，进一步提升内燃机综合性能。

📚2 运行结果

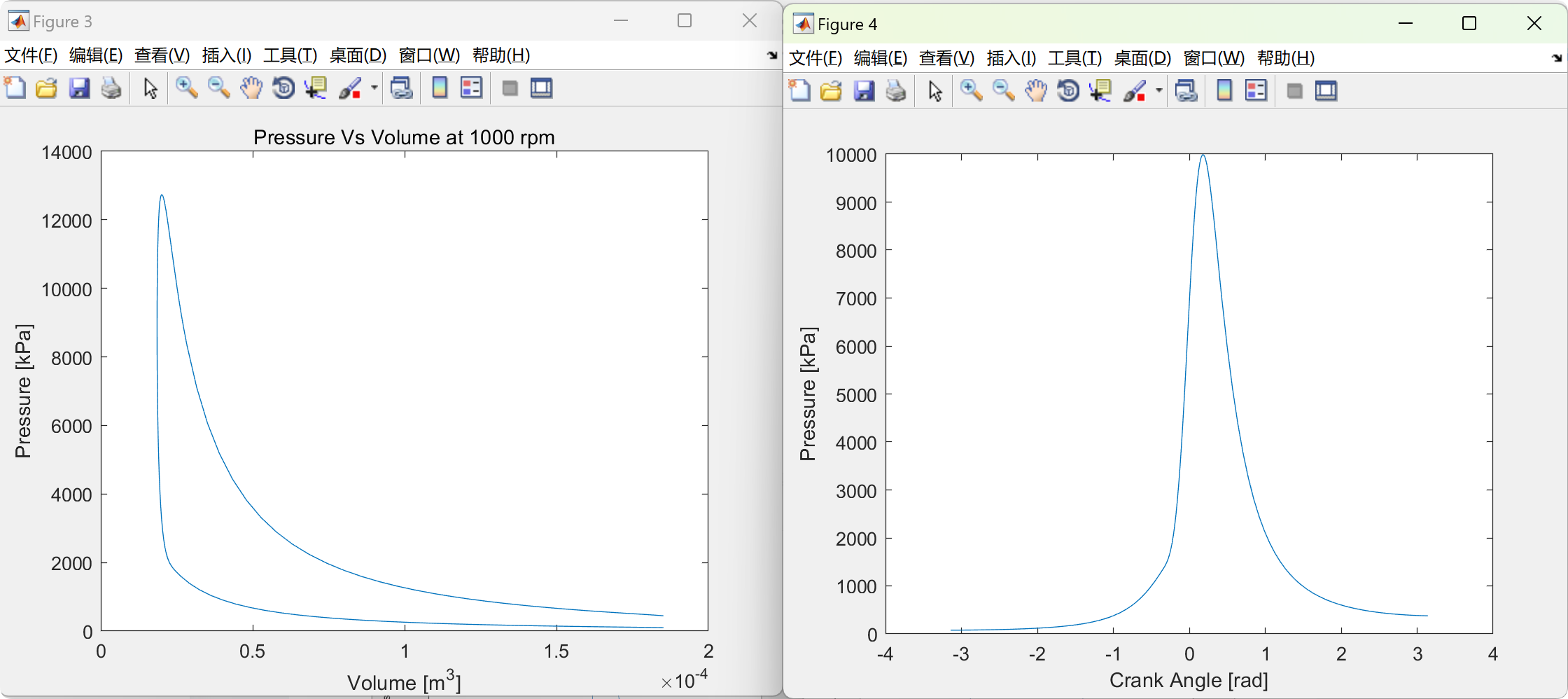
部分代码：

Rsp = 0.287;     %specific gas constant for air         [kJ/kg.K]
k  = 1.35;       %specific heat ratio                   [unitless]
Cv = Rsp/(k-1);  %specific heat capacity const volume   [kJ/kg.K]
Cp = k*Cv;       %specific heat capacity const pressure [kJ/kg.K]

%Define ambient conditions
Pa = 101.325;         %Ambient pressure          [kPa]
Ta = 333.15;          %Ambient temperature       [K]
rho_a  = Pa/(Rsp*Ta); %Ambient density           [kg/m^3]

%Temperature coming out of the intake pipe
T1 = Ta;       %Initial temperature       [K]

%Engine Geometric Parameters
np = 6;          %Number of cylinders       [unitless]
rc = 10;         %compression ratio         [unitless]

%Specify 2 of the following 3: Vd, B and L
Vd = 0.002;                    %Total displacement volume [m^3]
B  = .5*(4*Vd/(np*pi))^(1/3);     %Bore       [m]
L  =  4*B;%4*Vd/(np*pi*B^2);        %Stroke     [m]
a  = L/2;                      %crankshaft length [m]

%Specify either R (geometric ratio) or l (connecting rod length)
R  = 5.5;                      %Geometric ratio, l/a      [unitless]
l  = R*a;                      %Connecting rod length,    [m]

%Operational parameters
Nstart  = 1000;             %crankshaft rotational speed [rpm]
Nend    = 5000;     
Nnumber = 3;                %don't request fewer than 2 or the code will break
theta_s = -20;              %combustion timing angle [degrees]
theta_s = theta_s * pi/180; %convert angle to radians

%Fuel parameters
Qhv = 43400;                %Fuel heating value  [kJ/kg fuel]
AF  = 22;                   %A/F ratio           [unitless]
Qin = Qhv/(AF+1);           %Heat input,         [kJ/kg mixture]
theta_d = 40;               %combustion duration [degrees]
theta_d = theta_d*pi/180;   %convert angle to radians

%Cooling parameters
Tinf= 85+273;                %Coolant/Wall Temperature [K]
Vbdc = (Vd/np)*(rc/(rc-1));  %BDC volume [m^3]
Vtdc = (Vd/np)*(1/(rc-1));   %TDC volume [m^3]
Ach  = 0.25*pi*B^2;          %Cylinder head surface area [m^2]
Ap   = Ach;                  %Piston crown  surface area [m^2]

%Intake geometry patterns
LD_intake = 1000; %L/D for intake [unitless]
epsD      = 0.01; %epsilon/D (roughness) of intake [unitless]
BD_intake = 1;    %B/D_intake [unitless]

%Valve Parameters
n_iv      = 2;    %Number of intake valves    [unitless]
n_ev      = 2;    %Number of exhaust valves   [unitless]
Te_min = 273+800; %minimum expected exhaust temperature [K]
N_max  = 8000;    %max crankshaft spe2d [RPM]

%TASK 3: CALCULATE THE REQUIRED VALVE DIAMETERS HERE *****LECTURE 10 slide 27
Up_avg_max = 2*L*N_max/60; %max average piston speed based on max crankshaft speed [m/s]
c_in   = sqrt(k*Rsp*1000*Ta);     %speed of sound in the inlet pipe
c_ex   = sqrt(k*Rsp*1000*Te_min); %speed of sound in the exhaust pipe
D_iv   = sqrt(4*1.3*B^2*Up_avg_max/c_in/pi)/n_iv;  %Diameter of intake valves  [m]
D_ev   = sqrt(4*1.3*B^2*Up_avg_max/c_ex/pi)/n_ev;  %Diameter of exhaust valves [m]