👨🎓个人主页
💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
文献来源:

交直流系统潮流计算及相互关联特性分析研究
随着交直流输电系统的网络结构日益复杂,传统的纯交流潮流算法受到挑战,国内外学者对此进行了研究。截至到目前,交直流系统的潮流算法分为两大类:统一计算和交替迭代计算4。直流输电系统平衡方程包括换流器的稳态方程以及相关控制方程,统一潮流算法将交流与直流平衡方程同时求解。与其不同,交替迭代算法将两者分离计算,第一步将直流线路作为等值PQ负荷,求解交流系统状态量;第二步求解直流系统状态量,将第一步求解得到的交流端电压设为恒定值[5]。
在交直流转换过程中,换流装置吸收的无功功率约为所传输的直流功率的-一半,其中逆变器吸收的无功功率更多,能达到60%左右[14-15]。在传统电压稳定性分析方法的基础上得知,若受端交流系统无功供给不足,交直流系统会发生严重的电压失稳现象,尤其是逆变站受端电网交直流混合节点。
目前来说,人们主要从静态、动态两个角度研究交直流系统电压稳定性问题。在静态电压稳定角度,分析方法包括最大功率曲线法、短路比法、电压稳定因子分析法、特征值分析、崩溃点法等。在动态电压稳定角度,分析方法包括动态最大功率曲线法、分叉理论法、时域仿真、暂态能量函数等6]。
对于潮流算法,合适的存储结构可实现元素的快速检索、更新、存储,提高计算速度。本章算法采用支路潮流微增量为基元,使支路与雅可比矩阵直接关联;采用三角检索存储格式,存储框架不改变,只在预留的位置添加注入元,避免了繁琐的信息检索[49]。
相对于消除全部直流变量方法来说,保留直流电流变量的交直流潮流计算方法增加了雅可比矩阵的维数,与纯交流的雅可比矩阵格式有差异,但关于状态量直流电流的导数项多数为0,矩阵的稀疏度依然较高。以交流潮流部分的存储技术为基础,为保持其雅可比格式最大化相容,该算法按照不同的控制方式,将直流输电线路等效成相应的节点与线路,在相应的存储数组上作相应的变化。
以文献[49]阐述的封闭存储框架为基础,阐述添加直流输电单元对存储检索技术的影响。以一条直流输电线路为例,整流器节点为i,逆变器节点k,分析在不同控制方式下存储格式的调整。假设n为电网总节点数,b为考虑虚拟支路的总支路数,直流输电单元个数分别为a,临时指针 pt,同时定义的各存储数组,变化如下:

一、交直流系统定义与结构
交直流混合系统由交流电网、直流电网及换流设备构成,其核心功能是实现交直流电能的双向高效转换与传输。典型结构包括:
- 交流系统:作为传统电力网络的基础,通过变压器、电抗器等设备与换流站连接,承担电能分配功能。例如,送端和受端交流系统通过电抗器、电容器等实现电压稳定。
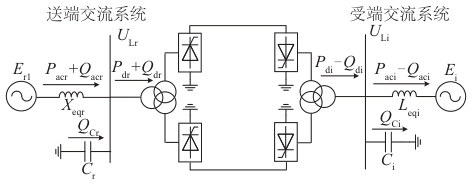
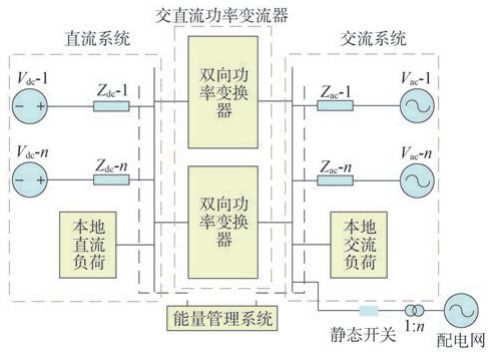
- 直流网络:包括柔性直流(如MMC-HVDC)和传统直流(如LCC-HVDC),通过换流器与交流系统互联。柔性直流网络采用多电平换流技术,具备无功功率独立调节能力。
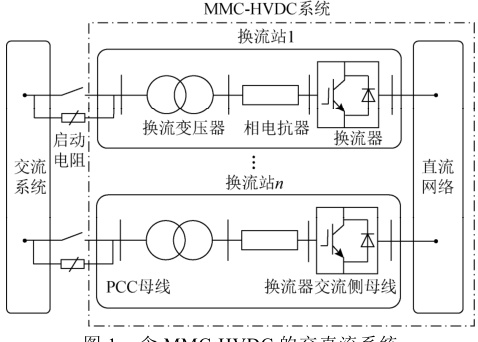
- 换流站:核心设备为换流变压器、相电抗器和换流器(VSC或LCC),实现交直流电能转换。公共连接点(PCC)母线负责多换流站的功率协调。
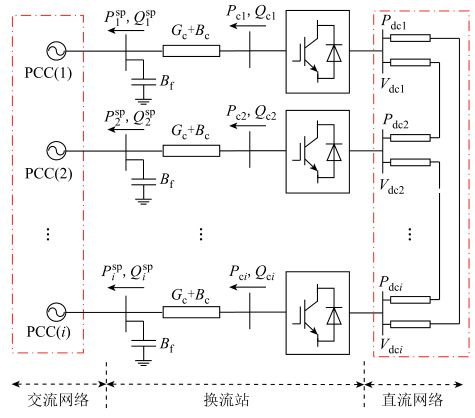
- 能量管理系统(EMS) :集成源网荷储协调控制,实现潮流优化、电能质量监测及经济调度。
二、交直流系统潮流计算原理与方法
1. 数学模型
-
交流系统:基于节点导纳矩阵,通过牛顿-拉夫逊法或PQ分解法求解电压幅值、相位及功率分布。
-
直流系统:需建立换流器方程,例如两端直流系统的电压-功率关系:

其中,Db为换流变压器参数,Rd为线路电阻,α为触发角。
-
换流器模型:VSC换流器需考虑脉宽调制(PWM)控制方式,其方程涉及直流电压、有功/无功功率的耦合。
2. 计算方法
- 统一迭代法:将交流与直流变量统一构建雅可比矩阵,收敛速度快但计算复杂度高。
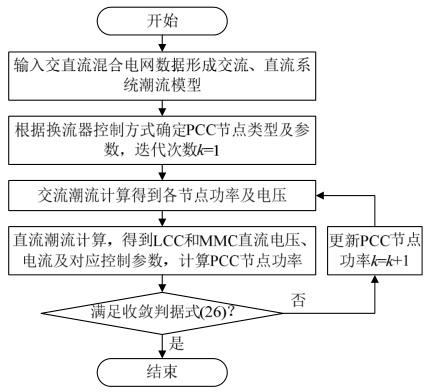
- 交替迭代法:分步求解交流与直流方程,适用于多控制策略场景。流程包括:初始化交流潮流→计算直流参数→更新PCC节点功率→迭代至收敛。
- 全纯嵌入法(HEM) :通过幂级数展开求解非线性方程,避免初值敏感性,适用于概率潮流分析。
- 概率潮流:采用蒙特卡洛模拟、多项式混沌展开(PCE)等方法处理风电出力不确定性。
3. 控制方式影响
- 定功率/定电压控制:增强电压相互作用强度,易导致换相失败。
- 定电流/定熄弧角控制:电压交互作用较弱,适用于稳定运行场景。
三、交直流系统相互关联特性
1. 交互作用因子(MIIF)
- 定义:衡量多馈入系统中直流子系统间电压波动的耦合程度。
- 影响因素:
- 电气距离:直流落点间距越小(联系阻抗ZijZij越低),MIIF越大。
- 交流系统强度:受端系统等值阻抗ZnjZnj越大(系统强度越弱),MIIF越高。
- 负荷特性:恒功率负荷的MIIF高于恒阻抗负荷。
2. 系统强度指标
- 多馈入短路比(MISCR) :与MIIF成反比,反映系统对直流功率扰动的承受能力。
- 控制方式影响:定功率控制会降低本地交流系统强度,增加电压失稳风险。
3. 动态交互问题
- 次同步振荡(SSO) :交直流参数(如线路阻抗、控制环参数)影响振荡传播特性。
- 故障恢复差异:机电-电磁混合仿真显示,故障恢复初期直流响应特性与纯机电仿真存在偏差。
四、现有研究进展与挑战
1. 研究热点
- 高效算法:交替迭代法结合稀疏矩阵技术,提升大规模系统计算效率。
- 概率潮流:全纯嵌入法与PCE结合,解决风电不确定性对潮流分布的影响。
- 多端直流系统:二阶锥规划(SOCP)将非凸优化问题转化为凸问题,实现最优潮流求解。
2. 技术挑战
- 模型复杂度:含多电力电子变压器(PET)的系统需建立端口耦合模型,解耦难度大。
- 计算效率:高维随机变量导致“维数灾”,限制PCE方法的应用。
- 控制策略协调:多换流站控制模式切换需动态调整潮流方程。
五、联合仿真工具与案例
1. 仿真工具
- 机电-电磁混合仿真:PSS/E(机电暂态)与PSCAD/EMTDC(电磁暂态)联合,适用于交直流故障分析。
- ADPSS平台:支持400回直流、10万节点的大规模仿真,具备并行计算能力。
- GPU加速技术:基于异构并行计算,提升电磁暂态仿真速度。
2. 典型案例
- 南方电网仿真:对比常规直流与柔性直流的故障响应,验证混合仿真精度。
- 内蒙古背靠背工程:通过PSModel实现异步联网,优化潮流分布。
- 湖北电网应用:高保真直流控制保护模型,解决接地极引线故障判别难题。
六、结论与展望
交直流系统潮流计算及关联特性分析是保障电网安全运行的核心技术。未来研究需聚焦:
- 多时间尺度建模:融合机电、电磁及市场动态模型,实现全景仿真。
- 人工智能融合:结合深度学习优化潮流预测与控制策略。
- 标准化与工程化:制定换流站控制接口标准,推动仿真工具国产化。
📚2 运行结果
2.1 整流侧定电流,逆变侧定电压

2.2 整流侧定电流,逆变侧定熄弧角

2.3 整流侧定功率,逆变侧定电压

2.4 整流侧定功率,逆变侧定熄弧角

2.5 整流侧定触发角,逆变侧定电流

部分代码:
%% 直流节点编号
D_CN=Hvdc.con(:,[1 2])';%直流节点编号
A_CN=setdiff(1:n,union(D_CN,SW.con(1,1)))';
N_DC=size(D_CN,1);%直流节点个数
N_AC=size(A_CN,1);%交流节点个数
P_N=setdiff(1:n,SW.con(1,1))';
Q_N=setdiff(P_N,PV.con(:,1));
P_N=intersect(A_CN, P_N);%交流节点P方程节点
Q_N=intersect(A_CN, Q_N);%交流节点Q方程节点
P=size(P_N,1); %交流节点P方程个数
Q=size(Q_N,1); %交流节点Q方程个数
% YK=zeros(P+Q);
DPa=zeros(P,1);
DQa=zeros(Q,1);
DPt=zeros(N_DC,1);
DQt=zeros(N_DC,1);
Dd1=zeros(N_DC,1);
Dd2=zeros(N_DC,1);
Dd3=zeros(N_DC,1);
Dd4=zeros(N_DC,1);
Dd5=zeros(1,1);
H=zeros(P+N_DC);
N=zeros(P+N_DC,Q+N_DC);
M=zeros(Q+N_DC,P+N_DC);
L=zeros(Q+N_DC);
JRX=zeros(9,9);
%% 直流迭代初值设置+控制方式
V_d=ones(N_DC,1)*1.1562;%直流电压初值
I_D=0.5;
% fai=ones(N_DC,1)*30/180*pi;%功率因数角初值30°
P_d=0.6.*ones(N_DC,1);
Qd=0.3.*ones(N_DC,1);
Sd=0.5.*ones(N_DC,1);
Control_ang=[20/180*pi;17/180*pi];%换流器控制角,第一个为alpha,第二个为gama
% Control_ang(2)=30/180*pi;
W=cos(Control_ang);
K_T=ones(N_DC,1);%直流支路两端变压器变比值设置
🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。
[1]王云鹏. 交直流系统潮流计算及相互关联特性分析[D].山东大学,2016.























 503
503

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








