基于快速探索随机树RRT和Dubins路径规划与避障研究（Matlab代码实现）-CSDN博客

本文链接：https://blog.csdn.net/Yan_she_He/article/details/147709243

👨‍🎓个人主页

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

一、RRT算法的基本原理与应用

1. 基本原理

2. 改进算法

3. 应用场景

二、Dubins路径规划的定义与数学特性

1. 定义

2. 局限性

三、RRT与Dubins路径的结合策略

1. 结合动机

2. 具体方法

3. 案例实现

四、避障技术与动态环境优化

1. 传感器融合

2. 动态避障策略

3. 改进算法

五、挑战与未来方向

1. 现有挑战

2. 未来方向

六、结论

📚2 运行结果

2.1 RRT

2.2 RRT_Dubins

2.3 RRT_obstacles

2.4 RRT_Dubins_obstacles

🎉3 参考文献

💥4 Matlab代码实现

💥1 概述

一、RRT算法的基本原理与应用

1. 基本原理

快速探索随机树算法

令 Tk 为一个有 K 个节点的 RRT，Q 为 Tk 的节点，Cfree 为与障碍物无碰撞的机器人自由状态空间。定义 Qinit 为初始状态即起点，Qgoal 为目标状态即终点。令 Qrand 为空间中一个随机选取的位姿状态，然后找出 Tk 中距离 Qrand 最近的节点Qnear。设p，q∈Cfree，令D( Qnear，Qrand) ≤D( Q，Qrand) 。在 Qrand 与 Qnear 连线上求 Qnew，Qnew 必须满足 Qnew ∈ Cfree 且 D( Qnear，Qrand) = ρ的条件，其中 ρ ＞ 0，为 RRT 生长的最小单位长度，称为步长。如果存在 Qnew，则 Tk 增加一个新节点; 否则重新选取 Qrand，重复以上过程。初始的 RRT 算法的构建过程如图 1 所示。

Dubins 理论

Dubins 于 1957 年提出了 Dubins 曲线理论，主要内容是在满足一定曲率条件下，连接同一平面内具有特定方向向量的任意两点的最短轨迹是曲线[20]。在没有其他约束因素的情况下，同一平

面上的任意两点的最短路径是直线，但是在有一定的曲率约束的情况下，最短的路径则是圆弧。

Dubins 曲线理论主要用来求解有曲率约束的最短路径。通过选择两条与两个圆相切的切线中的一

条，可以得到 Dubins 路径，其中起始和终止位置都在圆弧上。圆弧的半径是曲率半径，它由无人

系统的转弯半径决定，圆弧中心就是曲率中心，于是该问题就简化为寻找两个圆弧的公切线。两

圆之间有两种公切线：内切线、外切线。在给定位姿点下，无人系统可以向左转和向右转，路径可以以顺时针方向和逆时针方向结束。一个给定的位姿点上有两种转弯方式，因此有两个相切圆，如图 3 所示。一个向右转弯，在弧段 C1上标记 R ，另一个是向左转弯，在弧段 C2 上标记 L ，一个位姿点可以产生 4 条 Dubins 路径。即 LSL， LSR， RSL ，RSR ，如图 4 所示。

RRT（快速探索随机树）是一种基于采样的路径规划算法，由Steven M. Lavalle于1998年提出。其核心思想是通过随机采样和树状扩展探索高维空间，逐步构建从起点到目标的可行路径。算法流程包括：

随机采样：在配置空间中随机选取目标点。
最近邻搜索：在现有树中找到距离目标点最近的节点。
扩展与碰撞检测：向目标方向扩展步长，若新节点无碰撞则加入树中。
迭代收敛：重复直到路径到达目标或达到最大迭代次数。

2. 改进算法

RRT*：引入重连接机制，优化路径长度和平滑度，实现渐近最优。
RRT-smart*：结合智能采样策略，减少冗余节点并优化路径直线性。
Informed RRT*：通过椭圆区域限制采样空间，加速收敛。
双向RRT（RRT-Connect） ：从起点和目标点双向生长树，提升效率。

3. 应用场景

机器人导航：适用于非凸、高维环境下的避障。
无人机航迹规划：结合滚动窗口策略处理未知环境。
自动驾驶：优化轨迹以最小化能量消耗或转弯半径。

二、Dubins路径规划的定义与数学特性

1. 定义

Dubins路径是满足最小转弯半径约束的最短路径，由直线段（S）和圆弧段（L/R，左/右转）组成，共有6种类型（如LSL、RSR等）。其数学特性包括：

曲率约束：路径需满足最大曲率（即最小转弯半径）。
几何组合：通过微分几何原理生成连续路径。

2. 局限性

路径不连续性：圆弧与直线连接处的曲率突变，需车辆停顿调整转向。
动态适应性差：仅适用于静态环境，需结合其他算法处理动态障碍。

三、RRT与Dubins路径的结合策略

1. 结合动机

运动学约束：Dubins路径确保生成的路径满足车辆转弯半径限制。
全局探索能力：RRT的高效采样弥补Dubins在复杂环境中的路径搜索不足。

2. 具体方法

RRT-Dubins：在RRT扩展时用Dubins曲线替代直线连接，确保运动学可行性。
Dubins RRT*：通过重连接机制优化路径质量，并引入启发式函数加速收敛。
动态环境适应：结合滚动窗口和动态检测机制，实时更新路径以避开移动障碍。

3. 案例实现

MATLAB仿真：通过替换RRT的边为Dubins曲线，生成平滑路径。
机械臂规划：利用Dubins曲线优化RRT*生成的轨迹，解决路径抖动问题。

四、避障技术与动态环境优化

1. 传感器融合

多传感器协同：激光雷达（精度高）结合超声波（低成本）和视觉（环境建模），提升障碍物检测鲁棒性。
数据融合算法：如D-S证据理论加权融合多源数据，减少误检。

2. 动态避障策略

实时重规划：检测到动态障碍后，快速调用RRT*或人工势场法重新规划路径。
预测与规避：通过历史轨迹预测障碍物运动，提前调整路径。

3. 改进算法

目标导向采样：以概率偏向目标点，减少随机性并提升收敛速度。
动态步长调整：根据环境复杂度自适应调整扩展步长，平衡探索与避障效率。

五、挑战与未来方向

1. 现有挑战

计算复杂度：高维空间下RRT的实时性不足，需硬件加速或并行计算。
动态环境适应性：多障碍物协同避障仍依赖全局重规划，效率较低139。
T-RO | 动态混乱环境中无人机的快速自适应感知与规划，仅凭单个雷达在人群中稳定飞行

01:31

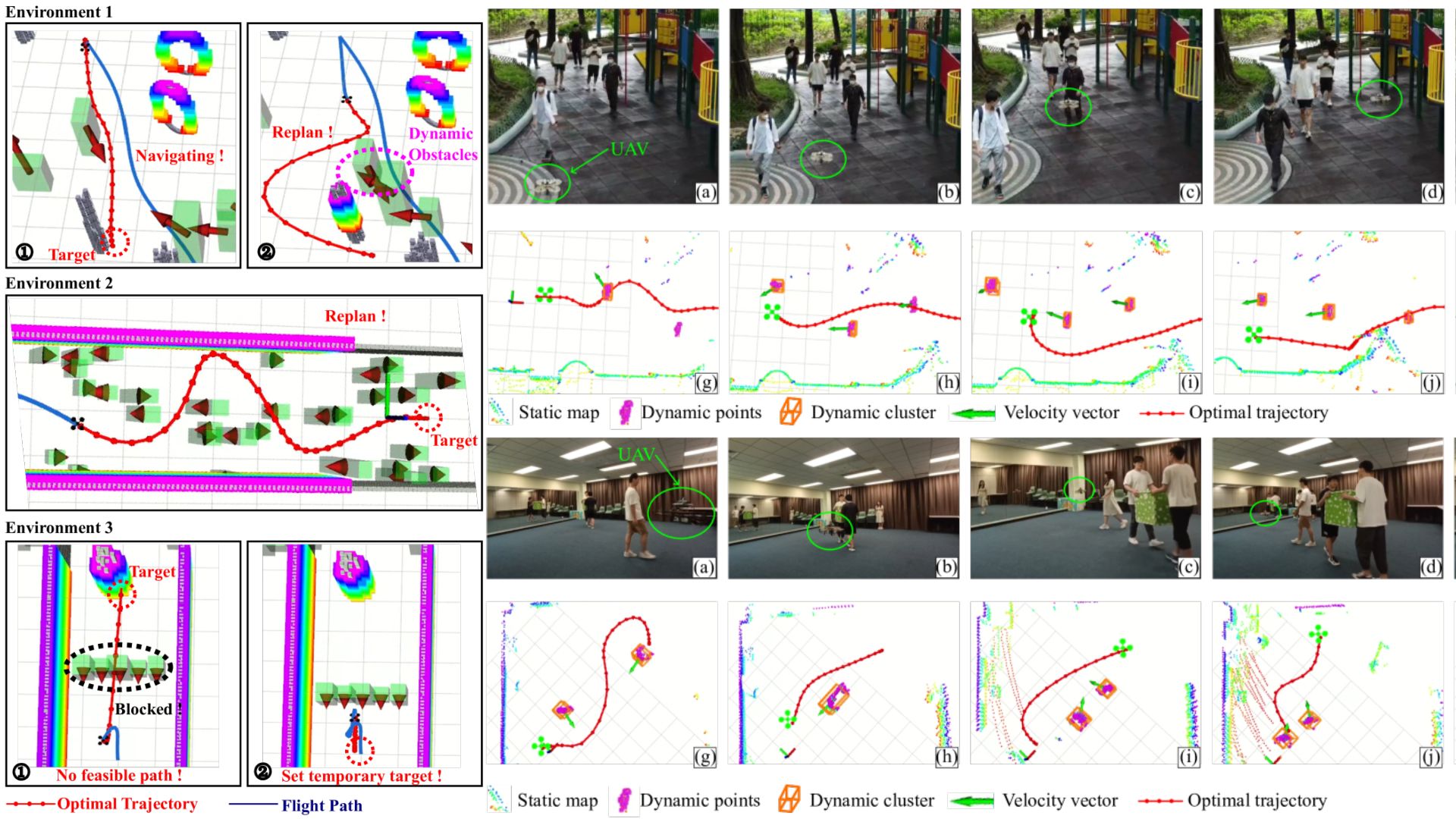
2. 未来方向

深度学习融合：利用卷积神经网络（CNN）学习环境特征，优化采样策略。
多智能体协同：研究多机器人路径分配与避碰策略。
在线优化：结合模型预测控制（MPC）实现动态环境下的实时轨迹跟踪138。
轨迹优化｜矩形增量膨胀安全走廊构建算法(附ROS C++/Python实现)

六、结论

RRT与Dubins路径的结合有效解决了运动学约束下的路径规划问题，在机器人、无人机和自动驾驶领域展现出广泛应用潜力。未来通过算法优化与多技术融合（如深度学习、多传感器协同），有望进一步提升复杂环境下的规划效率与安全性。

📚2 运行结果

2.1 RRT

2.2 RRT_Dubins

2.3 RRT_obstacles

2.4 RRT_Dubins_obstacles

部分代码：

main_fig_name = 'RRT with dubins curve and obstacle detection';
close(findobj('type','figure','name',main_fig_name));

%%%%%%%%%%%%%%%%%%%% User Configuration Area %%%%%%%%%%%%%%%%%%%%
% define the map
map.height = 20;
map.width = 20;
map.center = [0, 0];
map.offset = map.center - [map.width, map.height]./2; % bottom-left corner

% starting vertex
origin = [1,2, 20*pi/180];

% define the obstacles using polygones, should be a cell stack of arrays.
poly = { [-4,-4; -1.5, -4; 0, -2.5; -0.5, -1; -3, 0],...
[0,3; 3,3; 3, 6; 4, 6; 1.5, 8; -1, 6; 0, 6] };

% RRT parameters
iteration = 1000;
th_range = 2*pi; % do not change without knowledge about Dubins
th_center = 0;
th_offset = 0;

% dubins parameters
turning_rad = 0.5;
exp = 0.2;
%%%%%%%%%%%%%%%%%%%% End of configuration area %%%%%%%%%%%%%%%%%%%%
% main program starts here
poly = poly_verify(poly, map);
if ~iscell(poly)
error("Ending due to incorrect obsticle polygon setting");
return;
end

% prelocation of data
edges.x = zeros(iteration,2);
edges.y = zeros(iteration,2);
edges.th = zeros(iteration,2);
edges.param(iteration).p_init = [0, 0, 0]; % the initial configuration
edges.param(iteration).seg_param = [0, 0, 0]; % the lengths of the three segments
edges.param(iteration).r = turning_rad; % model forward velocity / model angular velocity turning radius
edges.param(iteration).type = -1; % path type. one of LSL, LSR, ...
edges.param(iteration).flag = 0;

% initial conditions, DO NOT CHANGE
vertecies = origin;
vert_count = 1;
ind_nearest = zeros(iteration,1);
edge_count = 0;

% figure('name', 'RRT growing'); % originally for real-time animation
tic;
for i=1:iteration
% random point generation
x_rand = map.width*rand() + map.offset(1);
y_rand = map.height*rand() + map.offset(2);
th_rand = th_range*rand() + th_offset;

% check if (x,y) is available or not
if chk_xy_available([x_rand,y_rand], map, poly) == 0
continue;
end


% connect to nearest point
[ind_nearest(i),param_nearest] = dubins_searchn(vertecies, [x_rand, y_rand, th_rand], turning_rad);

% check availablility, see dubins_core.m for more info
if( param_nearest.flag < 0)
continue; % goto next loop, reset i doesn't work in MATLAB
elseif( chk_dubins_collision(param_nearest, map, poly, exp)==0 )
%%%%%%%%%%%%%%%%% edit line %%%%%%%%%%%%%%%%
% append the newly generated point and edge to the existing list
vertecies(vert_count+1,:) = [x_rand, y_rand, th_rand];
vert_count = vert_count + 1;