鲁棒优化（3）-yalmip+guobi的小例子

最新推荐文章于 2025-03-20 22:12:42 发布

Yudibrother

最新推荐文章于 2025-03-20 22:12:42 发布

阅读量4.2k

点赞数 9

本文链接：https://blog.csdn.net/Yudibrother/article/details/116237753

版权

鲁棒优化机会约束股票投资 Gamma选择概率公式

关键词由CSDN通过智能技术生成

前言

前面我们已经介绍了，连续线性模型的鲁棒对等转换全部过程，本章内容分两部分.
1.将鲁棒优化与机会约束结合，从概率的角度，选取Γ的大小，并给出一个简单易行的公式.
2.结合实例，直观的阐述鲁棒优化的过程.实例选取股票的投资和回报问题

一、如何选择Γ的大小

在Bertsimas和Sim，2004的文章，The price of Robustness中通过中心极限定理给出了概率公式.过程非常复杂，所以本文直接给出结论公式.
在这里插入图片描述
J是不确定向量的维度。概率由标准正态分布函数计算得出.
大概有0.35的概率不被违背

二、股票投资问题

设有150只股票，n=150，投资的期望回报和偏离期望的标准差分别为
在这里插入图片描述
求解以下问题

其中，标准差是不确定的向量.
之前我们设定目标函数中不能含有不确定变量，所以进行如下等式转换

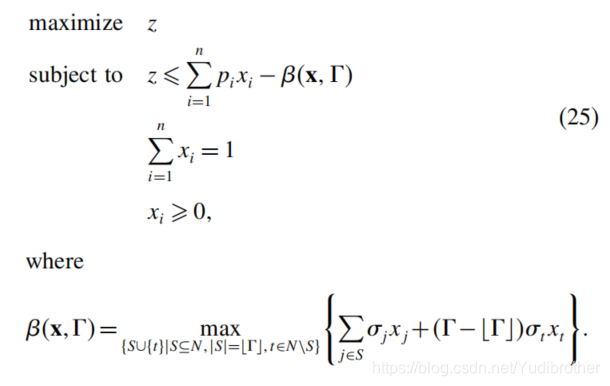
将其转换为鲁棒对等模型

for i = 1 : 150
    p(i) = 1.15 + (0.05 / 150) * i; %计算期望
    sigam(i) = (0.05 / 450) * (2 * i * 150 * 151) ^ 0.5; %计算标准差
end
%设置决策变量
t = sdpvar(1, 1);
x = sdpvar(1, 150); %股票投资比例
gama = 5 * ones(1, 150); %控制保守度
m = sdpvar(1, 150); %对偶变量
Q = sdpvar(1, 150); %对偶变量
%%写入相应的约束
st = [sum(x) == 1]; %投资比例之和等于1
for i = 1 : 150
    st = [st, sigam(1, i) * x(1, i) <= m(1, i) + Q(1, i), ...
        0 <= Q(1, i), ...
        0 <= x(1, i), ...
        0 <= m(1, i), ...
        t <= p * x' - m(1, i) * gama(1, i) - sum(Q)]; %...表示换行
end
optimize(st, -t)%求解
plot(1 : 150, value(x)); %画出投资比例图

在这里插入图片描述