GAMES101-计算机图形学学习笔记-Transformation

原视频教程链接：https://www.bilibili.com/video/BV1X7411F744

仿射变换

仿射变换 = 线性变换 + 平移

线性变换

缩放

$x^{\prime }=s_{x}x{y}^{\prime }=s_{y}y$

$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{cc}{s}_x& 0\\ 0& s_y\end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]$

错切变换

$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{cc}1& a\\ 0& 1\end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]$

旋转

默认为绕原点逆时针旋转


有如下性质：

$R_{-\theta }=\left[\begin{array}{cc}cos\theta & sin\theta \\ -sin\theta & cos\theta \end{array}\right]=R_{\theta }^T=R_{\theta }^{-1}$

像这种其逆矩阵等于转置矩阵的矩阵，在数学上定义为正交矩阵。

平移

$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{c}x\\ y\end{array}\right]+\left[\begin{array}{c}{t}_x\\ t_y\end{array}\right]$

齐次坐标

为了将两种变换统一表示，引入齐次坐标，增加一个维度w

故平移后：

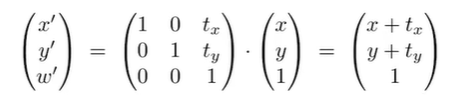
点与向量的表示
2D point: (x, y, 1)^T
2D vector: (x, y, 0)^T 具有平移不变性

且满足：
vector ± vector = vector
point - point = vector
vector + point = point

point + point : 结果为两点的中点，因为在齐次坐标中：
$\left[\begin{array}{c}x\\ y\\ w\end{array}\right]$ is a point $\left[\begin{array}{c}x/w\\ y/w\\ 1\end{array}\right](w\ne 0)$

逆变换
矩阵A经过M变换得到矩阵B，矩阵B则经过M^-1 变换回到A
证明：
MA = B = MM^-1 B
故 A = M^-1 B

由于矩阵的乘法是不满足交换律的，故变换的顺序十分重要
如旋转45°后向x方向平移1个单位:(从右至左结合)

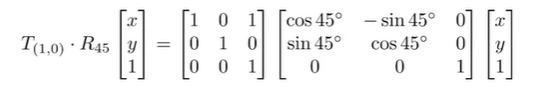
复杂的操作可分解成多次简单变换
如围绕点 c 旋转 α

变换矩阵为：$T(c)\cdot R(\alpha )\cdot T(-c)$

3D变换

use 4x4 matrix for affine transformations

旋转

由z到y旋转，$y\times z=x$

由z到x旋转，因为 $z\times x=y$，和另外两种情况旋转方向不一致，所以写法上有差异。

由x到y旋转，$x\times y=z$

绕轴n旋转α度 （n经过原点）

Viewing(观测) 变换

视角变换

一般将摄像机放在原点，y轴作为上方，看向-z。

通过变换矩阵$M_{view}$将其变换到目标状态，需要以下步骤：

• 将 e 移至原点
• 旋转 g 至 -Z
• 旋转 t 至 Y
• 旋转 (g x t) 至 X

$M_{view}=R_{view}{T}_{view}$

$R_{view}$不好直接求得，可先求得$R_{view}^{-1}$

$R_{view}^{-1}=\left[\begin{array}{cccc}{x}_{\hat{g}\times \hat{t}}& x_t& x_g& 0\\ y_{\hat{g}\times \hat{t}}& y_t& y_g& 0\\ z_{\hat{g}\times \hat{t}}& z_t& z_g& 0\\ 0& 0& 0& 1\end{array}\right]$

$R_{view}=\left[\begin{array}{cccc}{x}_{\hat{g}\times \hat{t}}& y_{\hat{g}\times \hat{t}}& z_{\hat{g}\times \hat{t}}& 0\\ x_t& y_t& z_t& 0\\ x_g& y_g& z_g& 0\\ 0& 0& 0& 1\end{array}\right]$

投影

正交投影

简单理解为：

• 摄像机看向 -Z，上方为Y轴
• 丢弃模型的 Z 轴
• 缩放到 $[-1,1{]}^2$ 的矩形中

更正式的做法：
将任意立方体转化为标准立方体

透视投影

将视锥体压成一个立方体，再进行正交投影

根据相似三角形原理，可求得：$y^{\prime }=\frac{n}{z}y,x^{\prime }=\frac{n}{z}x$

所以：
$M_{persp->ortho}\left[\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right]=\left[\begin{array}{c}nx\\ ny\\ unknown\\ z\end{array}\right]$

$M_{persp->ortho}=\left[\begin{array}{cccc}n& 0& 0& 0\\ 0& n& 0& 0\\ ?& ?& ?& ?\\ 0& 0& 1& 0\end{array}\right]$

近平面上所有的点位置不会发生改变，带入z=n

$\left[\begin{array}{c}x\\ y\\ n\\ 1\end{array}\right]=>\left[\begin{array}{c}nx\\ ny\\ n^2\\ n\end{array}\right]$

可求出第三列为$\left[\begin{array}{cccc}0& 0& A& B\end{array}\right]$

且 $An+B=n^2$

代入远平面中点，同理可得：$Af+B=f^2$

求解可得：$A=n+f,B=-nf$

至此，求得：
$M_{persp->ortho}=\left[\begin{array}{cccc}n& 0& 0& 0\\ 0& n& 0& 0\\ 0& 0& n+f& -nf\\ 0& 0& 1& 0\end{array}\right]$