球面坐标系转换为笛卡尔坐标系

今天又遇到了球面坐标系转换成笛卡尔坐标系，其实是一个很简单的问题，记录一下以便以后查看。

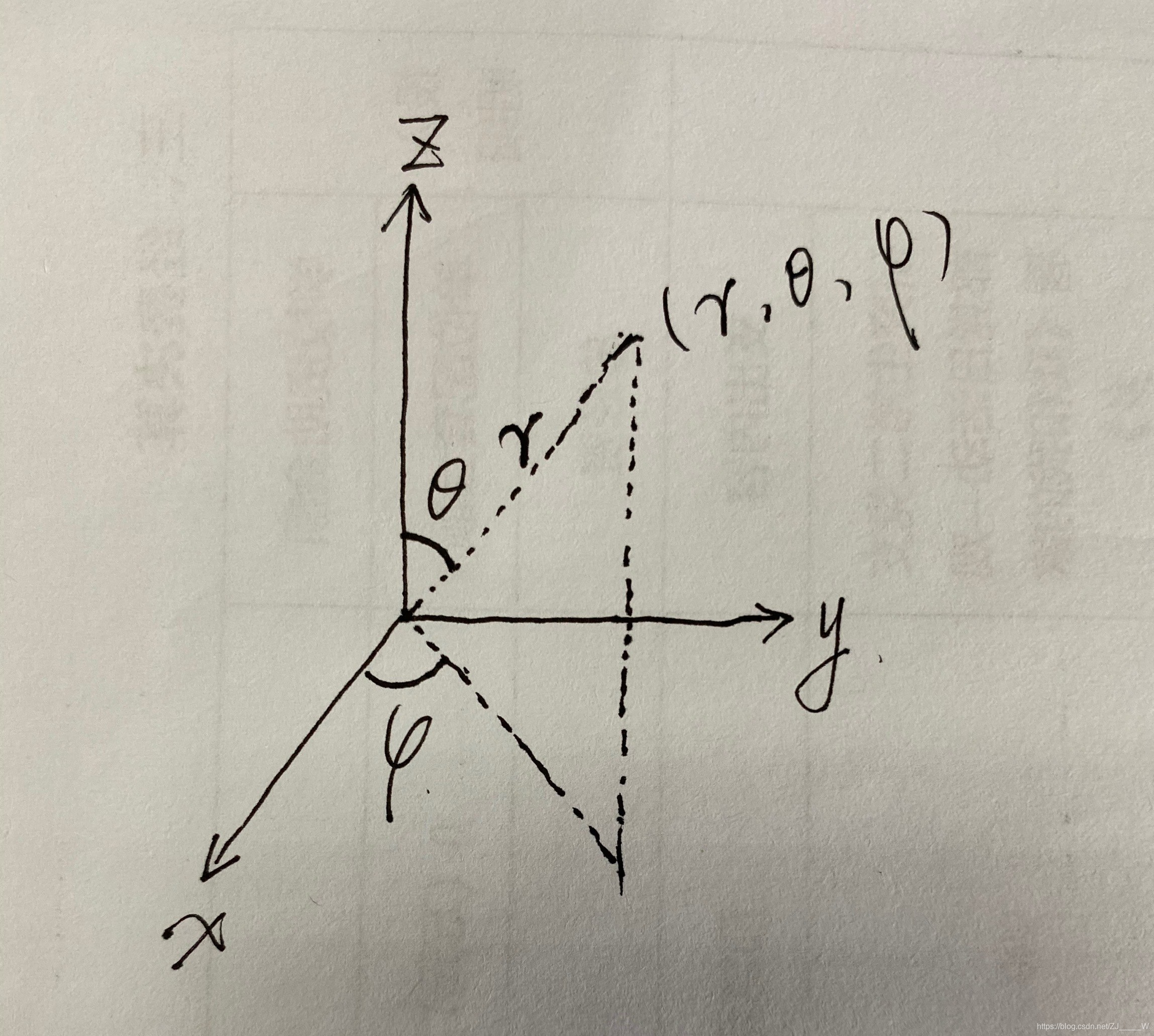
假设球面坐标系中的P点坐标为（r，$\theta$, $\phi$）有时候球面坐标系中的三个坐标会使用另一种方式表达：

r：无疑就是球体的半径
$\theta$：称为倾斜角（inclination）
$\phi$：称为方位角（azimuth）

将球体坐标系转换为笛卡尔坐标系（也就是常见的xyz坐标系）：
x=rsin（$\theta$）cos（$\phi$）
y=rsin（$\theta$）sin（$\phi$）
z=r*cos（$\theta$）

用C#代码写出来：

    public Vector3 ToCartesian()
    {
        Vector3 cartesian = new Vector3();
        cartesian.z = radius * Mathf.Sin(inclination) * Mathf.Cos(azimuth);
        cartesian.x = radius * Mathf.Sin(inclination) * Mathf.Sin(azimuth);
        cartesian.y = radius * Mathf.Cos(inclination);
        return cartesian;
    }