本系列笔记为方便日后自己查阅而写,更多的是个人见解,也算一种学习的复习与总结,望善始善终吧~
一阶常系数微分方程
Au= dudt
将一阶常系数微分方程转换为线性代数问题的关键在于常系数微分方程的解一定是指数形式的。那么我们的需要求解的东西就是指数的系数和指数的幂,而这可以转换为线性代数问题。
解的指数形式通常是自然常数 e 的指数(猜测是因为时域信号可以转到频域,傅里叶变换,这方面学识浅薄)
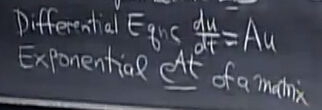
这个形式很容易让我们联想到之前对于矩阵
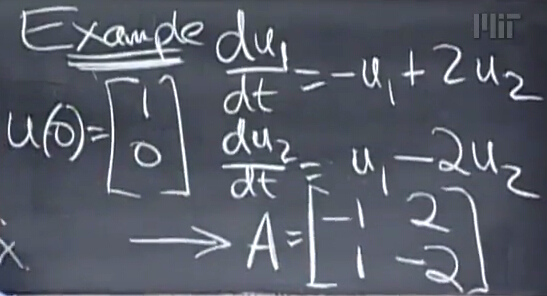
这里问题被转换为了求解 Au= dudt
特征值与特征向量
先找 A 的特征值和特征向量
求解特征值
两个小技巧:
- 行列式determinant为特征值的积
- 矩阵的迹trace为特征值的和
当然可以直接求解determinant=0得到特征值:

由于老师直接剧透
求解特征向量
两个小技巧:
- 对于特征值为0,特征向量即为null space,free variable自由变量置1很容易求得
- 对于另一个特征值-3,利用
A−λI 特征向量不变,也可以转换为求解null space解的形式
解会是上面这样的形式,证明:
带入之前的公式 dudt








 这篇博客探讨了一阶常系数微分方程与线性代数的关系,强调了解的指数形式与矩阵A的特征值、特征向量的关联。通过特征值分析,解释了系统稳定性条件,并介绍了泰勒级数展开理解eAt的矩阵形式,为解耦和求解微分方程提供理论基础。
这篇博客探讨了一阶常系数微分方程与线性代数的关系,强调了解的指数形式与矩阵A的特征值、特征向量的关联。通过特征值分析,解释了系统稳定性条件,并介绍了泰勒级数展开理解eAt的矩阵形式,为解耦和求解微分方程提供理论基础。
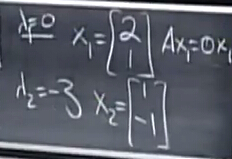
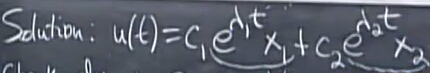
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章















 817
817

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








