齐次裁剪
通过透视投影得到的点
[
x
齐
次
,
y
齐
次
,
z
齐
次
,
w
]
[x_{齐次},y_{齐次},z_{齐次},w]
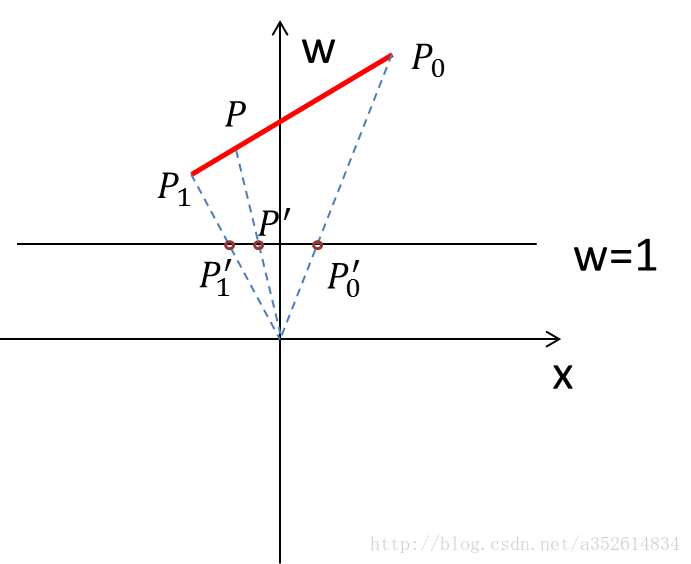
[x齐次,y齐次,z齐次,w]形成的三角形片元,裁剪是在齐次}坐标中做裁剪的,即它是一个四维空间的裁剪。而不是经过透视除法后的立方体空间
[
x
齐
次
/
w
,
y
齐
次
/
w
,
z
齐
次
/
w
,
1
]
[x_{齐次}/w,y_{齐次}/w,z_{齐次}/w,1]
[x齐次/w,y齐次/w,z齐次/w,1]。
假设view空间中点
P
0
(
x
,
y
,
z
)
P_0(x,y,z)
P0(x,y,z)投影后齐次坐标
P
1
(
x
′
,
y
′
,
z
′
,
w
)
P_1(x',y',z',w)
P1(x′,y′,z′,w)
view空间到齐次坐标转换关系为
P
1
=
M
p
e
r
s
p
e
c
t
i
v
e
P
0
P_1=M_{perspective}P_0
P1=MperspectiveP0
仿射变换不改变原来坐标系下顶点的属性(纹理,颜色)关系,所以可以直接线性插值。z’和z,y’和y,x’和x是线性关系。
P
2
(
x
′
′
,
y
′
′
,
z
′
′
,
1
)
=
(
x
′
/
w
,
y
′
/
w
,
z
′
/
w
,
1
)
P_2(x'',y'',z'',1)=(x'/w,y'/w,z'/w,1)
P2(x′′,y′′,z′′,1)=(x′/w,y′/w,z′/w,1),x’‘与x不是线性的关系,x’'与x,z有关系,经过透视除法后,不能使用线性插值,否则进行插值的纹理坐标或者颜色会不准确。
{
−
1
≤
x
齐
次
/
w
≤
1
−
1
≤
y
齐
次
/
w
≤
1
−
1
≤
z
齐
次
/
w
≤
1
→
{
−
w
≤
x
齐
次
≤
w
−
w
≤
y
齐
次
≤
w
−
w
≤
z
齐
次
≤
w
\left\{ \begin{array}{c} -1\le x_{齐次}/w \le 1\\ -1\le y_{齐次}/w \le 1\\ -1\le z_{齐次}/w \le 1 \end{array} \right.\to \left\{ \begin{array}{c} -w\le x_{齐次} \le w\\ -w\le y_{齐次} \le w\\ -w\le z_{齐次} \le w\\ \end{array} \right.
⎩⎨⎧−1≤x齐次/w≤1−1≤y齐次/w≤1−1≤z齐次/w≤1→⎩⎨⎧−w≤x齐次≤w−w≤y齐次≤w−w≤z齐次≤w
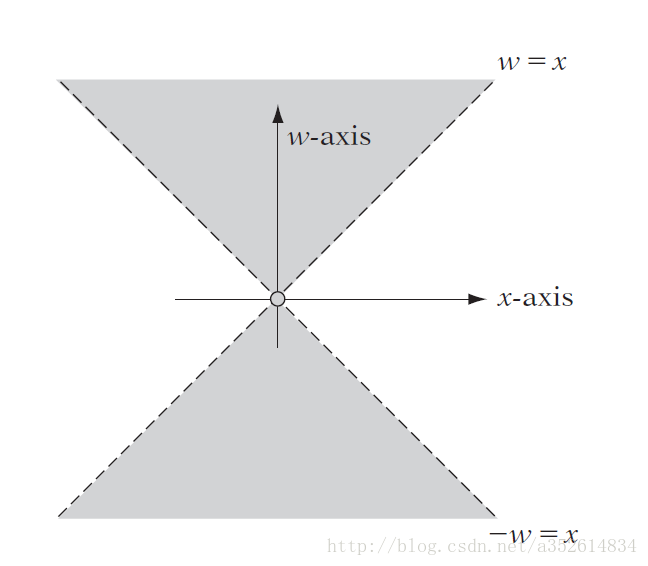
六个平面分别为
w
=
x
齐
次
w
=
−
x
齐
次
w
=
y
齐
次
w
=
−
y
齐
次
w
=
z
齐
次
w
=
−
z
齐
次
\begin{array}{c} w = x_{齐次}\\ w = -x_{齐次}\\ w = y_{齐次}\\ w = -y_{齐次}\\ w = z_{齐次}\\ w = -z_{齐次}\\ \end{array}
w=x齐次w=−x齐次w=y齐次w=−y齐次w=z齐次w=−z齐次
假设相机空间的二个点
a
(
x
0
,
y
0
,
z
0
,
u
0
,
v
0
,
c
0
)
a(x_0,y_0,z_0,u_0,v_0,c_0)
a(x0,y0,z0,u0,v0,c0),
b
(
x
1
,
y
1
,
z
1
,
u
1
,
v
1
,
c
o
l
o
r
1
)
b(x_1,y_1,z_1,u_1,v_1,color_1)
b(x1,y1,z1,u1,v1,color1),透视变换后齐次坐标的点
a
′
(
x
0
′
,
y
0
′
,
z
′
0
,
w
0
′
,
u
0
,
v
0
,
c
0
)
a'(x'_0,y'_0,z'0,w'_0,u_0,v_0,c_0)
a′(x0′,y0′,z′0,w0′,u0,v0,c0),
b
′
(
x
1
′
,
y
1
′
,
z
1
′
,
w
1
′
,
u
1
,
v
1
,
c
o
l
o
r
1
)
b'(x'_1,y'_1,z'_1,w'_1,u_1,v_1,color_1)
b′(x1′,y1′,z1′,w1′,u1,v1,color1)
假设与-1左平面即
w
=
−
x
齐
次
w=-x_{齐次}
w=−x齐次,交点为
c
′
=
a
′
+
t
(
b
′
−
a
′
)
c' = a'+t(b'-a')
c′=a′+t(b′−a′),w,x分量为
(
w
0
′
+
t
(
w
1
′
−
w
0
′
)
,
x
0
′
+
t
(
x
1
′
−
x
0
′
)
)
(w'_0+t(w'_1-w'_0), x'_0+t(x'_1-x'_0))
(w0′+t(w1′−w0′),x0′+t(x1′−x0′))带入平面解得t,然后线性插值uvc。
固定yz。w=x和w=-x把平面分成二个区域。w<0说明在相机的背一侧。
光栅化
把透视除后的规格化设备坐标系按照窗口的长宽通过平移缩放变换到屏幕坐标系。
从一个投影场景生成网格颜色样本。1600宽,1200高的显示器有1 920 000个像素点。通常每个像素点会计算几次(深度比较),费时间。
FrameBuffer
Framebuffer是一个2D的图像,每个像素点都有颜色值。 用于显示在屏幕的图像数据。
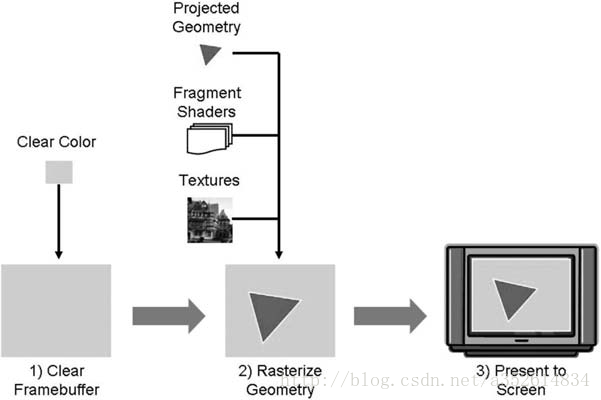
光栅化一个三角形流程
- 确定被三角形覆盖的可见像素
- 计算三角形内的每个像素的颜色
- 确定像素的最终颜色并上传到framebuffer
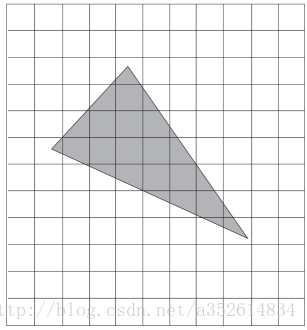
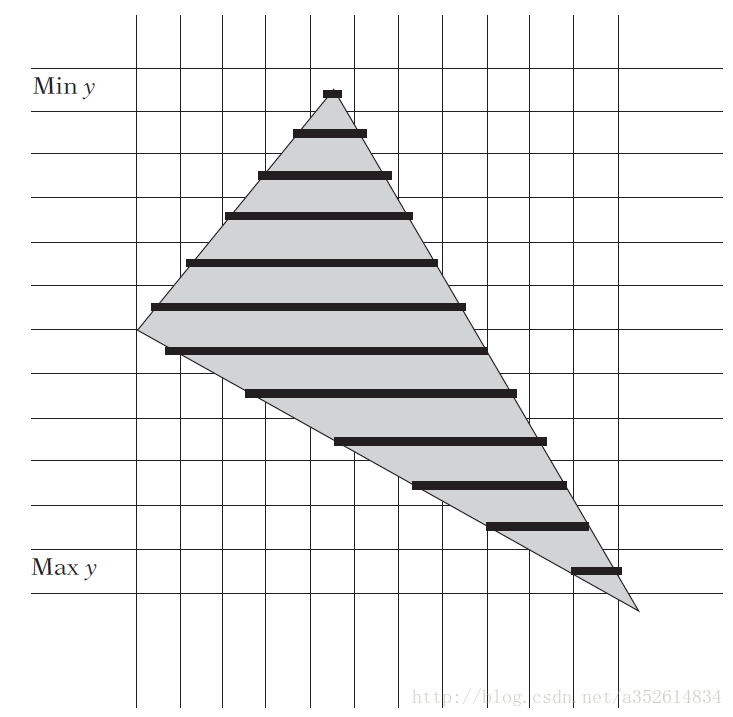
黑色的代表完整的片元,灰色的代表不完整的片元。
如何把三角形变成片元?
可以采用扫描线,根据三角形凸的性质,水平扫描线从一段进入,另一端出去,在边缘和上下顶点处是部分片元。y最大值,最小值是三个顶点的最大值和最小值。
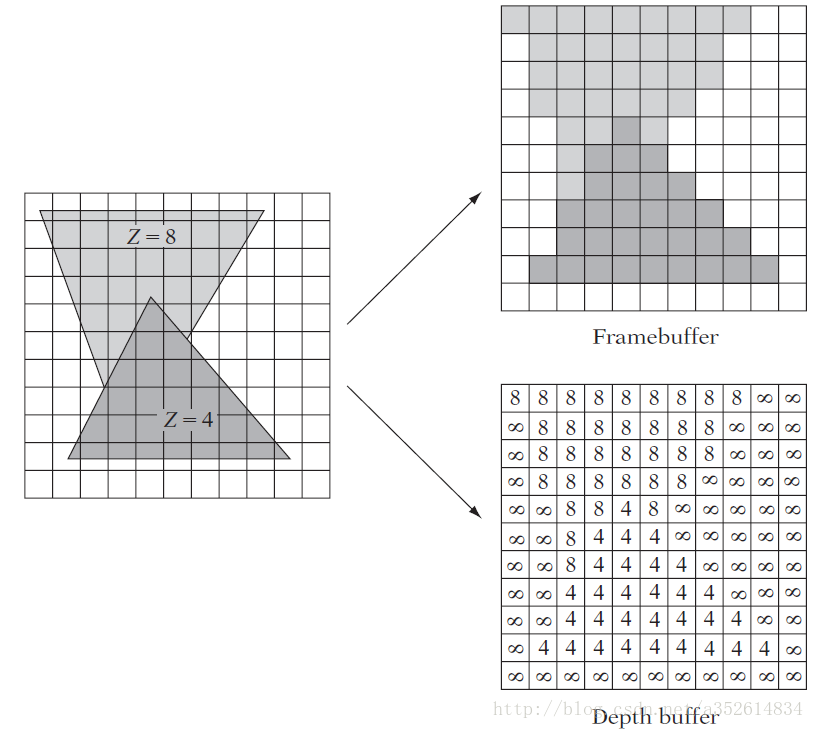
深度缓存
深度缓存用来确定可见的三角片,如果当前片元比原来的近,替换,否则不替换。但是当二个深度是一样时,会有显示问题。
缺点:
- 每个像素点有一个深度数组
- 在每一帧需要初始化为背景颜色,深度缓存为背景深度
以上二个硬件实现, 现在不是问题。对每一个片元的额外操作,计算深度值,查找深度缓存表,比较,写入如果符合。
z
n
d
c
z_{ndc}
zndc可以用来做深度值
假设视图空间一个三角形三角平面法向量
n
^
=
(
a
,
b
,
c
,
)
\hat n=(a,b,c,)
n^=(a,b,c,),平面可以表示成
a
x
+
b
y
+
c
z
+
d
=
0
ax+by+cz+d=0
ax+by+cz+d=0,d是一个固定常量。
平面上一点
(
x
v
i
e
w
,
y
v
i
e
w
,
z
v
i
e
w
)
(x_{view},y_{view},z_{view})
(xview,yview,zview)
该点在平面上,即:
a
x
v
i
e
w
+
b
y
v
i
e
w
+
c
z
v
i
e
w
+
d
=
0
ax_{view}+by_{view}+cz_{view}+d=0
axview+byview+czview+d=0
n
^
⋅
(
x
v
i
e
w
,
y
v
i
e
w
,
z
v
i
e
w
)
+
d
=
0
\hat n\cdot (x_{view},y_{view},z_{view}) + d=0
n^⋅(xview,yview,zview)+d=0
在NDC坐标中点
(
x
n
d
c
,
y
n
d
c
)
(x_{ndc}, y_{ndc})
(xndc,yndc)对应的视图空间坐标为一条射线
(
x
v
i
e
w
,
y
v
i
e
w
,
z
v
i
e
w
)
=
t
r
=
(
x
n
d
c
,
y
n
d
c
,
−
d
i
s
t
)
t
t
≥
0
(x_{view},y_{view},z_{view})=t\mathbf r=(x_{ndc},y_{ndc},-dist)t\quad t\ge 0
(xview,yview,zview)=tr=(xndc,yndc,−dist)tt≥0
dist表示到观察点到投影平面的距离。虽然能够对投影矩阵求逆,但是不能通过ndc坐标(即经过透视除法后的点)求的view的坐标。
视图空间的一个点投影在这个屏幕点上必定在这条射线上。
n
^
⋅
(
t
r
)
+
d
=
0
→
t
=
−
d
n
^
r
\hat {\mathbf n}\cdot (t\mathbf r) + d=0\to t=\dfrac{-d}{\hat {\mathbf n}\mathbf r}
n^⋅(tr)+d=0→t=n^r−d
(
x
v
i
e
w
,
y
v
i
e
w
,
z
v
i
e
w
)
=
t
r
=
t
(
x
n
d
c
,
y
n
d
c
,
−
d
i
s
t
)
=
−
d
n
^
⋅
r
(
x
n
d
c
,
y
n
d
c
,
−
d
i
s
t
)
=
−
d
(
x
n
d
c
,
y
n
d
c
,
−
d
i
s
t
)
n
^
⋅
(
x
n
d
c
,
y
n
d
c
,
−
d
i
s
t
)
=
−
d
(
x
n
d
c
,
y
n
d
c
,
−
d
i
s
t
)
a
∗
x
n
d
c
+
b
∗
y
n
d
c
−
c
∗
d
i
s
t
→
z
v
i
e
w
=
d
∗
d
i
s
t
a
∗
x
n
d
c
+
b
∗
y
n
d
c
−
c
∗
d
i
s
t
(x_{view},y_{view},z_{view})=t\mathbf r=t(x_{ndc},y_{ndc},-dist)= \dfrac{-d}{\hat {\mathbf n}\cdot\mathbf r}(x_{ndc},y_{ndc},-dist)=\dfrac{-d(x_{ndc},y_{ndc},-dist)}{\hat {\mathbf n}\cdot (x_{ndc},y_{ndc},-dist)}=\dfrac{-d(x_{ndc},y_{ndc},-dist)}{a*x_{ndc}+b*y_{ndc}-c*dist}\to z_{view}=\dfrac{d*dist}{a*x_{ndc}+b*y_{ndc}-c*dist}
(xview,yview,zview)=tr=t(xndc,yndc,−dist)=n^⋅r−d(xndc,yndc,−dist)=n^⋅(xndc,yndc,−dist)−d(xndc,yndc,−dist)=a∗xndc+b∗yndc−c∗dist−d(xndc,yndc,−dist)→zview=a∗xndc+b∗yndc−c∗distd∗dist
{
z
v
i
e
w
≥
D
e
p
t
h
B
u
f
f
e
r
更新片元
z
v
i
e
w
<
D
e
p
t
h
B
u
f
f
e
r
不更新片元
→
{
1
z
v
i
e
w
≤
D
e
p
t
h
B
u
f
f
e
r
更新片元
1
z
v
i
e
w
>
D
e
p
t
h
B
u
f
f
e
r
不更新片元
\left\{ \begin{array}{c} z_{view}\ge DepthBuffer\qquad \text{更新片元}\\ z_{view}\lt DepthBuffer\qquad \text{不更新片元} \end{array} \right.\to \left\{ \begin{array}{c} \dfrac{1}{z_{view}}\le DepthBuffer\qquad \text{更新片元}\\ \dfrac{1}{z_{view}}\gt DepthBuffer\qquad \text{不更新片元} \end{array} \right.
{zview≥DepthBuffer更新片元zview<DepthBuffer不更新片元→⎩⎪⎨⎪⎧zview1≤DepthBuffer更新片元zview1>DepthBuffer不更新片元
但是直接求
z
v
i
e
w
z_{view}
zview有些复杂,我们使它的倒数,
1
z
v
i
e
w
=
a
∗
x
n
d
c
+
b
∗
y
n
d
c
−
c
∗
d
i
s
t
d
∗
d
i
s
t
=
(
a
d
∗
d
i
s
t
)
x
n
d
c
+
(
a
d
∗
d
i
s
t
)
y
n
d
c
−
c
d
\dfrac{1}{z_{view}}=\dfrac{a*x_{ndc}+b*y_{ndc}-c*dist}{d*dist}=(\dfrac{a}{d*dist})x_{ndc}+(\dfrac{a}{d*dist})y_{ndc}-\dfrac{c}{d}
zview1=d∗dista∗xndc+b∗yndc−c∗dist=(d∗dista)xndc+(d∗dista)yndc−dc
括号中为常数。
x
n
d
x
,
y
n
d
c
x_{ndx},y_{ndc}
xndx,yndc到屏幕坐标
x
s
,
y
s
x_s,y_s
xs,ys的变换是一个仿射变换
即:
1
z
v
i
e
w
=
I
n
v
Z
(
x
s
,
y
s
)
=
f
x
s
+
g
y
s
+
h
\dfrac{1}{z_{view}}=InvZ(x_s,y_s)=fx_s+gy_s+h
zview1=InvZ(xs,ys)=fxs+gys+h
根据forward difference
I
n
v
Z
(
x
s
+
1
,
y
s
)
−
I
n
v
Z
(
x
s
,
y
s
)
=
f
(
x
s
+
1
)
+
g
y
s
+
h
−
(
f
x
s
+
g
y
s
+
h
)
=
f
InvZ(x_s+1,y_s)-InvZ(x_s,y_s)=f(x_s+1)+gy_s+h-(fx_s+gy_s+h)=f
InvZ(xs+1,ys)−InvZ(xs,ys)=f(xs+1)+gys+h−(fxs+gys+h)=f
I
n
v
Z
(
x
s
,
y
s
+
1
)
−
I
n
v
Z
(
x
s
,
y
s
)
=
f
x
s
+
g
(
y
s
+
1
)
+
h
−
(
f
x
s
+
g
y
s
+
h
)
=
g
InvZ(x_s,y_s+1)-InvZ(x_s,y_s)=fx_s+g(y_s+1)+h-(fx_s+gy_s+h)=g
InvZ(xs,ys+1)−InvZ(xs,ys)=fxs+g(ys+1)+h−(fxs+gys+h)=g
得到:
I
n
v
Z
(
x
s
+
1
,
y
s
)
=
I
n
v
Z
(
x
s
,
y
s
)
+
f
InvZ(x_s+1,y_s)=InvZ(x_s,y_s)+f
InvZ(xs+1,ys)=InvZ(xs,ys)+f
I
n
v
Z
(
x
s
,
y
s
+
1
)
=
I
n
v
Z
(
x
s
,
y
s
)
+
g
InvZ(x_s,y_s+1)=InvZ(x_s,y_s)+g
InvZ(xs,ys+1)=InvZ(xs,ys)+g
通过这个公式,可以进行快速的
I
n
v
Z
InvZ
InvZ插值。
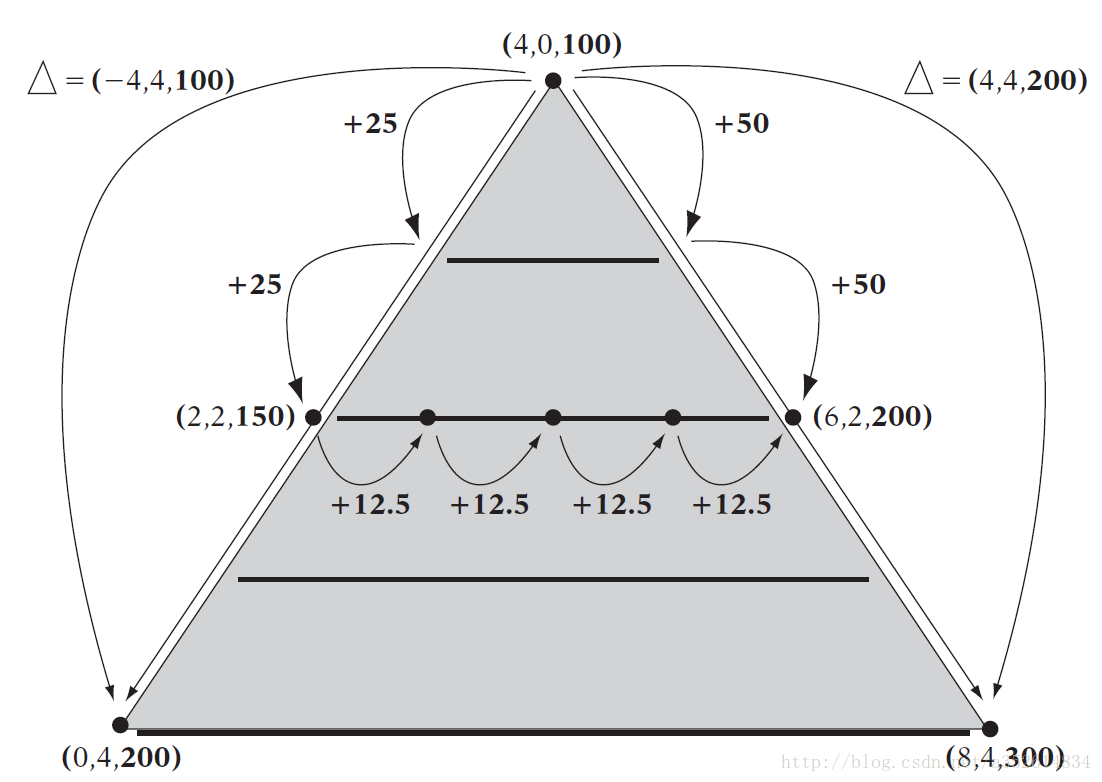
举个例子
常数
f
=
12.5
,
g
=
37.5
f=12.5,g=37.5
f=12.5,g=37.5
点
(
4
,
0
,
100
)
(4,0,100)
(4,0,100)正下方即金字塔第一条横线中间即以下4分别
(
4
,
1
,
137.5
)
,
(
4
,
2
,
175
)
,
(
4
,
3
,
212.5
)
,
(
4
,
4
,
250
)
(4,1,137.5),(4,2,175),(4,3,212.5),(4,4,250)
(4,1,137.5),(4,2,175),(4,3,212.5),(4,4,250)
z
n
d
c
z_{ndc}
zndc是
1
z
v
i
e
w
\dfrac{1}{z_{view}}
zview1的一个仿射变换(右手系,看向-z轴,归一化到[-1,1],
z
n
d
c
=
−
n
+
f
n
−
f
−
2
n
f
(
n
−
f
)
z
v
i
e
w
z_{ndc}=-\dfrac{n+f}{n-f}-\dfrac{2nf}{(n-f)z_{view}}
zndc=−n−fn+f−(n−f)zview2nf)
即
z
n
d
c
=
a
+
b
1
z
v
i
e
w
z_{ndc}=a+b\dfrac{1}{z_{view}}
zndc=a+bzview1
假设n(10),f(1000)映射到0,1
z
n
d
c
=
−
1000
99
∗
1
z
v
i
e
w
+
100
99
z_{ndc}=-\dfrac{1000}{99}*\dfrac{1}{z_{view}}+\dfrac{100}{99}
zndc=−991000∗zview1+99100
| z v i e w z_{view} zview | z n d c z_{ndc} zndc |
|---|---|
| 10 | 0.0 |
| 20 | 0.5 |
| 100 | 0.91 |
| 200 | 0.95 |
| 500 | 0.98 |
| 1000 | 1.0 |
可以看到$z_{view}$20的时候用掉了50%的精度,100的时候还剩下10%的精度。即前面的距离相机进的地方精度高,远的地方精度低,而远的地方可以会导致前后的物体映射到同一个z_{ndc}上,导致z-fighting。
16位的浮点数表示65535个数。
纹理映射
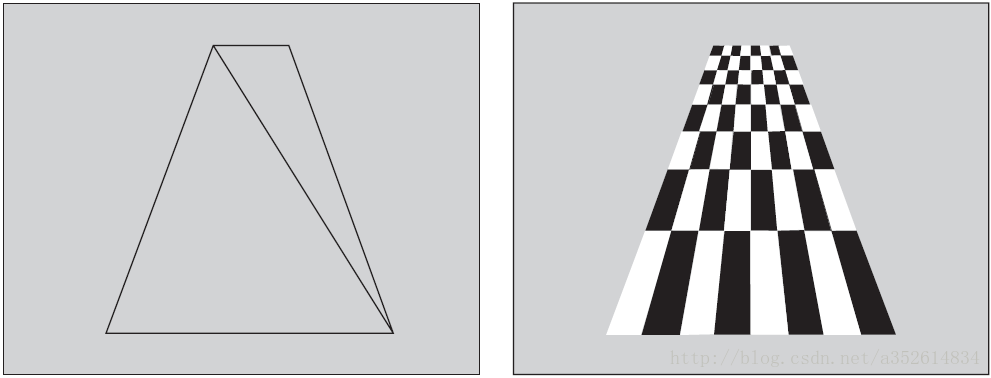
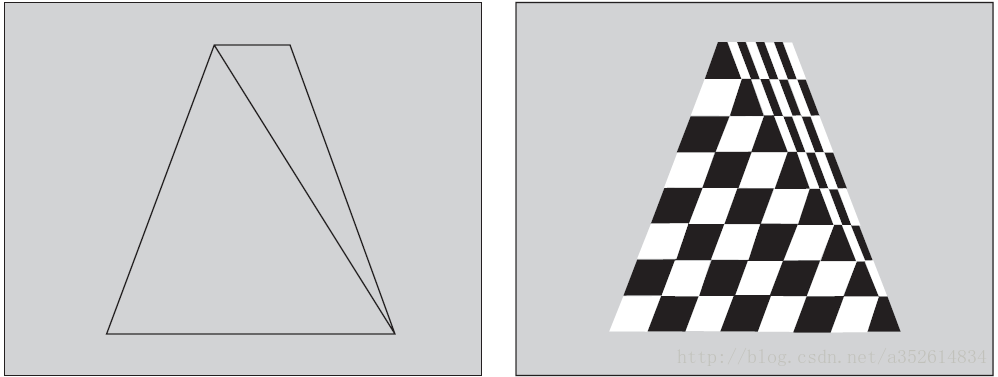
以下纹理映射的一个例子,沿着视线的方向。
线框图
纹理
期望的纹理映射
采用仿射变换的纹理映射
通常颜色的插值可以直接用线性插值,因为人对颜色变化不敏感。即认为用
x
s
c
r
e
e
n
,
y
s
c
r
e
e
n
x_{screen},y_{screen}
xscreen,yscreen(
x
s
c
r
e
e
n
,
y
s
c
r
e
e
n
与
x
n
d
c
,
y
n
d
c
是
线
性
关
系
x_{screen},y_{screen}与x_{ndc},y_{ndc}是线性关系
xscreen,yscreen与xndc,yndc是线性关系)去插值片元的颜色。
我们需要用View空间的位置去插值,而不是用ndc空间的值去插值。
x
n
d
c
,
y
n
d
c
x_{ndc},y_{ndc}
xndc,yndc与
u
z
n
d
c
,
v
z
n
d
c
uz_{ndc},vz_{ndc}
uzndc,vzndc成线性关系
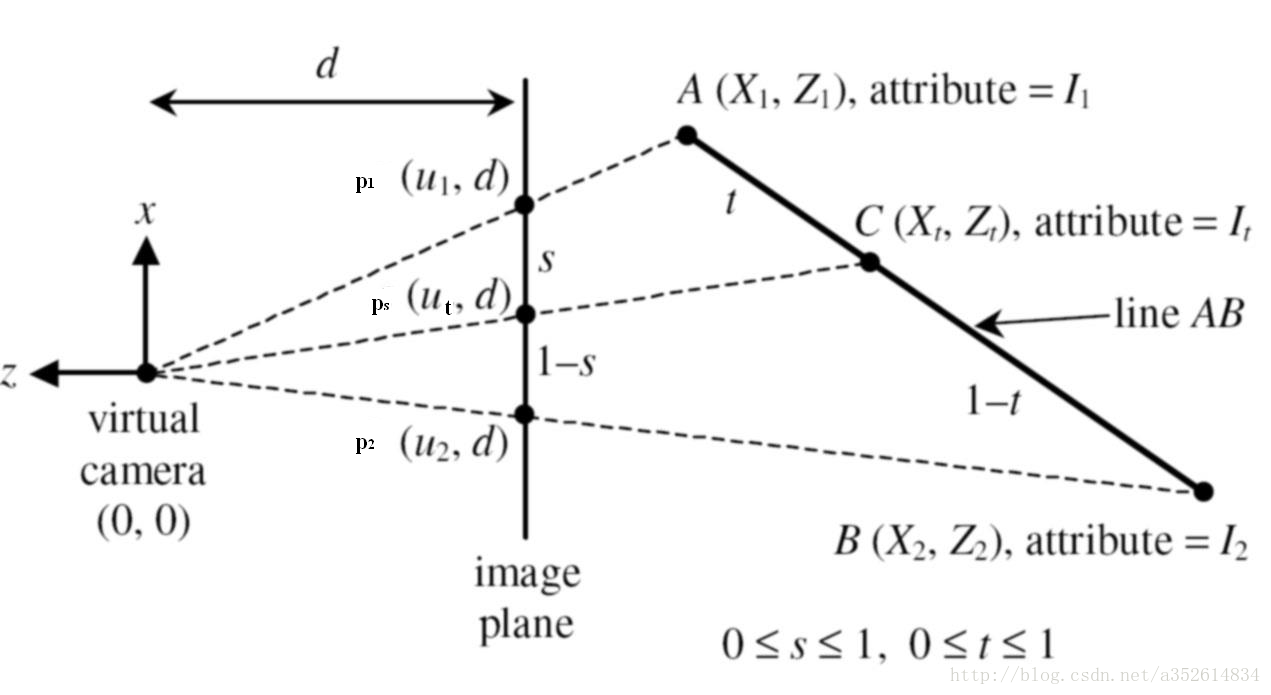
假设投影在xz平面上,yz平面的退到也类似。
假设View空间的二个点
A
(
X
v
i
e
w
1
,
Z
v
i
e
w
1
)
B
(
X
v
i
e
w
2
,
Z
v
i
e
w
2
)
A(X_{view1},Z_{view1})B(X_{view2},Z_{view2})
A(Xview1,Zview1)B(Xview2,Zview2),直线方程为
a
X
+
b
Z
=
c
aX+bZ=c
aX+bZ=c
投影平面的点
p
1
,
p
2
p_1,p_2
p1,p2在ndc上的点为
(
x
n
d
c
1
,
−
d
)
,
(
x
n
d
c
2
,
−
d
)
(x_{ndc1},-d),(x_{ndc2},-d)
(xndc1,−d),(xndc2,−d)
根据三角形相似得到:
X
v
i
e
w
1
Z
v
i
e
w
=
x
n
d
c
1
−
d
→
X
v
i
e
w
1
=
x
n
d
c
1
−
d
Z
v
i
e
w
1
\dfrac{X_{view1}}{Z_{view}}=\dfrac{x_{ndc1}}{-d}\to X_{view1}=\dfrac{x_{ndc1}}{-d}Z_{view1}
ZviewXview1=−dxndc1→Xview1=−dxndc1Zview1
把该点
(
x
n
d
c
1
−
d
Z
v
i
e
w
1
,
Z
v
i
e
w
1
)
(\dfrac{x_{ndc1}}{-d}Z_{view1},Z_{view1})
(−dxndc1Zview1,Zview1)带入直线方程
a
X
+
b
Z
=
c
aX+bZ=c
aX+bZ=c得到:
a
x
n
d
c
1
−
d
Z
v
i
e
w
1
+
b
Z
v
i
e
w
1
=
c
→
1
Z
v
i
e
w
1
=
−
a
d
c
x
n
d
c
1
+
b
c
a\dfrac{x_{ndc1}}{-d}Z_{view1}+bZ_{view1}=c\to \dfrac{1}{Z_{view1}}=-\dfrac{a}{dc}x_{ndc1}+\dfrac{b}{c}
a−dxndc1Zview1+bZview1=c→Zview11=−dcaxndc1+cb
同理另外一点为:
1
Z
v
i
e
w
2
=
−
a
d
c
x
n
d
c
2
+
b
c
\dfrac{1}{Z_{view2}}=-\dfrac{a}{dc}x_{ndc2}+\dfrac{b}{c}
Zview21=−dcaxndc2+cb
假设
p
s
=
p
1
+
s
(
p
2
−
p
1
)
,
0
<
s
<
1
p_s=p_1+s(p_2-p_1),0<s<1
ps=p1+s(p2−p1),0<s<1即
p
s
(
(
1
−
s
)
x
n
d
c
1
+
s
x
n
d
c
2
,
−
d
)
p_s((1-s)x_{ndc1}+sx_{ndc2},-d)
ps((1−s)xndc1+sxndc2,−d)
1
Z
s
=
−
a
d
c
x
s
+
b
c
=
−
a
d
c
(
(
1
−
s
)
x
n
d
c
1
+
s
x
n
d
c
2
)
+
b
c
=
(
1
−
s
)
(
−
a
d
c
x
n
d
c
1
+
b
c
)
+
s
(
−
a
d
c
x
n
d
c
2
+
b
c
)
=
(
1
−
s
)
1
Z
v
i
e
w
1
+
s
1
Z
v
i
e
w
2
\dfrac{1}{Z_{s}}=-\dfrac{a}{dc}x_{s}+\dfrac{b}{c}= -\dfrac{a}{dc}((1-s)x_{ndc1}+sx_{ndc2})+\dfrac{b}{c}= (1-s)(-\dfrac{a}{dc}x_{ndc1}+\dfrac{b}{c})+s(-\dfrac{a}{dc}x_{ndc2}+\dfrac{b}{c})=(1-s)\dfrac{1}{Z_{view1}}+s\dfrac{1}{Z_{view2}}
Zs1=−dcaxs+cb=−dca((1−s)xndc1+sxndc2)+cb=(1−s)(−dcaxndc1+cb)+s(−dcaxndc2+cb)=(1−s)Zview11+sZview21
可以知道:
x
n
d
c
x_{ndc}
xndc与
1
Z
v
i
e
w
\dfrac{1}{Z_{view}}
Zview1是线性关系,即
x
n
d
c
=
A
0
1
Z
v
i
e
w
+
B
0
,
Z
v
i
e
w
=
A
1
x
n
d
c
+
B
1
x_{ndc}=A_0\dfrac{1}{Z_{view}}+B_0,Z_{view}=A_1x_{ndc}+B_1
xndc=A0Zview1+B0,Zview=A1xndc+B1
在View空间中三角形纹理坐标(u,v)与空间中的点(X,Y,Z)呈线性关系,即
{
X
v
i
e
w
=
A
2
u
+
B
2
Y
v
i
e
w
=
A
3
u
+
B
3
\left\{ \begin{array}{c} X_{view}=A_2u+B_2\\ Y_{view}=A_3u+B_3 \end{array} \right.
{Xview=A2u+B2Yview=A3u+B3
带入:
X
v
i
e
w
=
x
n
d
c
−
d
Z
v
i
e
w
X_{view}=\dfrac{x_{ndc}}{-d}Z_{view}
Xview=−dxndcZview
得到:
A
2
u
+
B
2
=
x
n
d
c
−
d
Z
v
i
e
w
→
A
2
u
Z
v
i
e
w
+
B
2
Z
v
i
e
w
=
−
1
d
x
n
d
c
→
1
Z
v
i
e
w
=
A
0
x
n
d
c
+
B
0
A
2
u
Z
v
i
e
w
+
B
2
(
A
0
x
n
d
c
+
B
0
)
=
−
1
d
x
n
d
c
→
u
Z
v
i
e
w
=
A
x
n
d
c
+
B
A_2u+B_2=\dfrac{x_{ndc}}{-d}Z_{view}\to\\ \dfrac{A_2u}{Z_{view}}+\dfrac{B_2}{Z_{view}}= -\dfrac{1}{d}x_{ndc}\xrightarrow{\dfrac{1}{Z_{view}}=A_0x_{ndc}+B_0}\\ \dfrac{A_2u}{Z_{view}}+B_2(A_0x_{ndc}+B_0)= -\dfrac{1}{d}x_{ndc}\to \dfrac{u}{Z_{view}}=Ax_{ndc}+B
A2u+B2=−dxndcZview→ZviewA2u+ZviewB2=−d1xndcZview1=A0xndc+B0ZviewA2u+B2(A0xndc+B0)=−d1xndc→Zviewu=Axndc+B
同理有
u
Z
v
i
e
w
=
A
y
n
d
c
+
B
v
Z
v
i
e
w
=
A
x
n
d
c
+
B
v
Z
v
i
e
w
=
A
y
n
d
c
+
B
\dfrac{u}{Z_{view}}=Ay_{ndc}+B\\ \dfrac{v}{Z_{view}}=Ax_{ndc}+B\\ \dfrac{v}{Z_{view}}=Ay_{ndc}+B
Zviewu=Ayndc+BZviewv=Axndc+BZviewv=Ayndc+B
纹理映射总结
x
n
d
c
∼
1
Z
v
i
e
w
X
v
i
e
w
∼
u
X
v
i
e
w
=
x
n
d
c
−
d
Z
v
i
e
w
→
u
Z
v
i
e
w
∼
x
n
d
c
x_{ndc}\sim\dfrac{1}{Z_{view}}\\ X_{view}\sim u\\ X_{view}=\dfrac{x_{ndc}}{-d}Z_{view}\to\dfrac{u}{Z_{view}}\sim x_{ndc}\\
xndc∼Zview1Xview∼uXview=−dxndcZview→Zviewu∼xndc
因为
x
n
d
c
x_{ndc}
xndc到屏幕是一个仿射变换,
x
n
d
c
∼
x
s
c
r
e
e
n
→
u
Z
v
i
e
w
∼
x
s
c
r
e
e
n
x_{ndc}\sim x_{screen}\to\dfrac{u}{Z_{view}}\sim x_{screen}
xndc∼xscreen→Zviewu∼xscreen
对于屏幕上二个点
(
x
s
c
r
e
e
n
1
,
y
s
c
r
e
e
n
1
,
z
n
d
c
1
,
u
1
,
v
1
)
,
(
x
s
c
r
e
e
n
2
,
y
s
c
r
e
e
n
2
,
z
n
d
c
2
,
u
2
,
v
2
)
(x_{screen1},y_{screen1},z_{ndc1},u_1,v_1),(x_{screen2},y_{screen2},z_{ndc2},u_2,v_2)
(xscreen1,yscreen1,zndc1,u1,v1),(xscreen2,yscreen2,zndc2,u2,v2),插值点,先通过
z
n
d
c
1
,
z
n
d
c
2
插
值
得
到
z
n
d
c
′
即
1
Z
v
i
e
w
′
,
根
据
u
1
z
n
d
c
1
,
u
2
z
n
d
c
2
插
值
得
到
u
′
z
n
d
c
′
,
最
后
计
算
u
′
=
u
′
z
n
d
c
′
z
n
d
c
′
z_{ndc1},z_{ndc2}插值得到z_{ndc}'即\dfrac{1}{Z_{view}'},根据u_1z_{ndc1},u_2z_{ndc2}插值得到u'z_{ndc}',最后计算u'=\dfrac{u'z_{ndc}'}{z_{ndc}'}
zndc1,zndc2插值得到zndc′即Zview′1,根据u1zndc1,u2zndc2插值得到u′zndc′,最后计算u′=zndc′u′zndc′
纹理滤波
通过纹理坐标取得纹理图像的值。
纹理放大,显示像素比纹理像素尺寸大。
纹理缩小,显示像素比纹理像素尺寸小。
纹理放大
通过上面计算的纹理坐标u,v([0,1])乘上纹理尺寸后uv会有小数,采样可以采用如下二种方法:
- 最近邻插值
( u i n t , v i n t ) = ( f l o o r ( u t e x e l + 0.5 ) , f l o o r ( v t e x e l + 0.5 ) ) (u_{int},v_{int})=(floor(u_{texel}+0.5),floor(v_{texel}+0.5)) (uint,vint)=(floor(utexel+0.5),floor(vtexel+0.5))
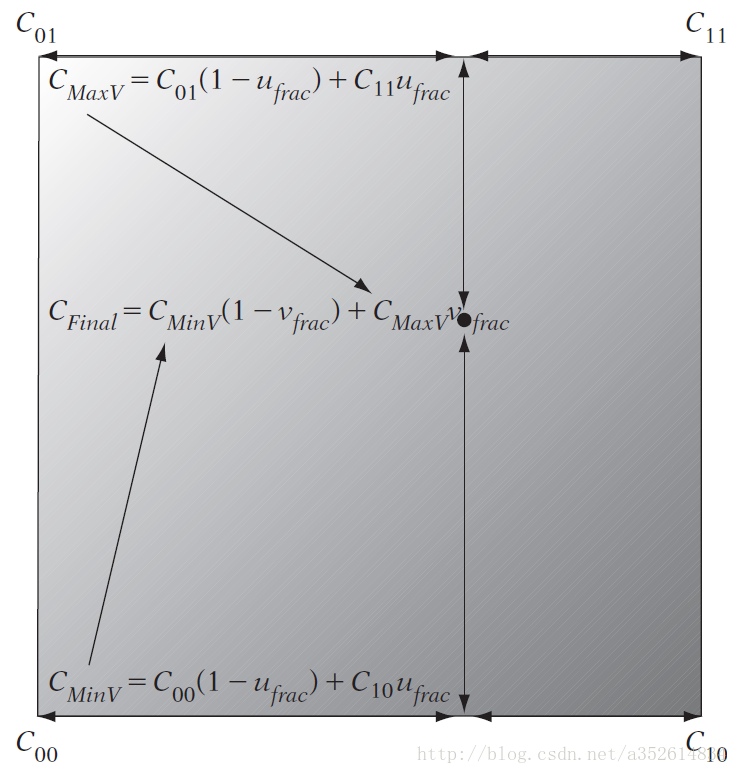
- 双线性滤波
左下角纹理坐标 ( u i n t , v i n t ) = ( f l o o r ( u t e x e l ) , f l o o r ( v t e x e l ) ) (u_{int},v_{int})=(floor(u_{texel}),floor(v_{texel})) (uint,vint)=(floor(utexel),floor(vtexel))
( u f r a c , v f r a c ) = ( u t e x e l − u i n t , v t e x e l − v i n t ) (u_{frac},v_{frac})=(u_{texel}-u_{int},v_{texel}-v_{int}) (ufrac,vfrac)=(utexel−uint,vtexel−vint)
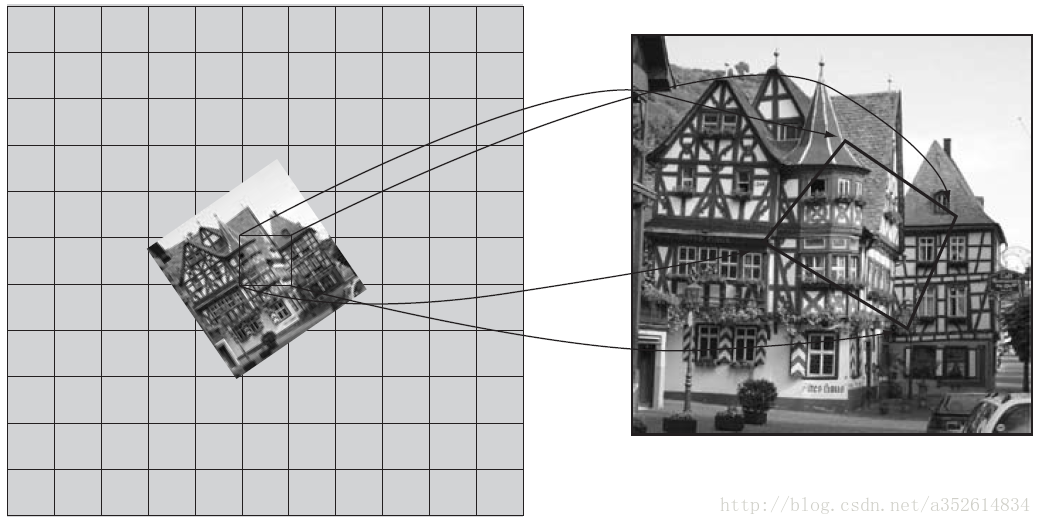
纹理缩小
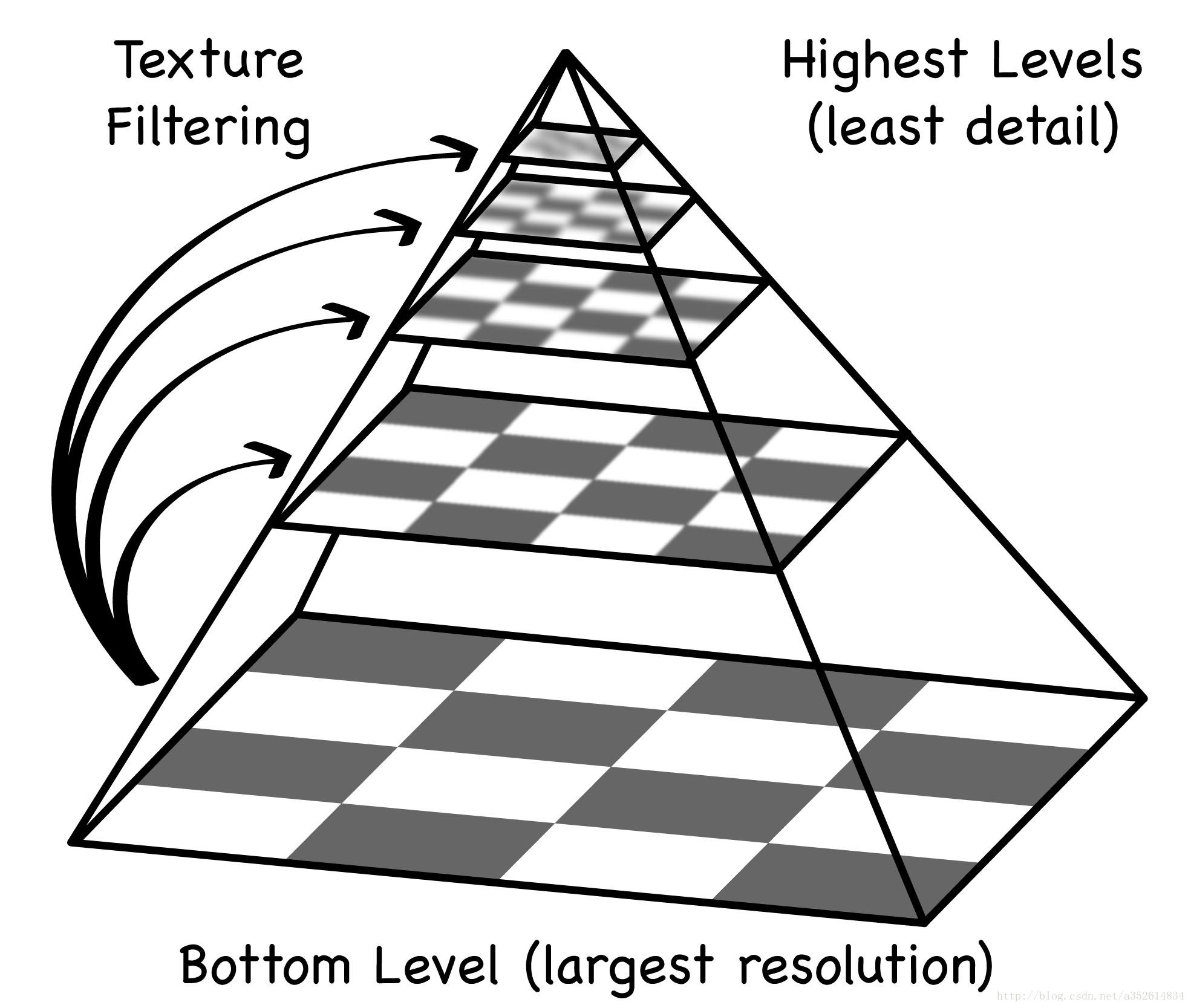
3. Mipmapping
原始图像Image0尺寸
w
t
e
x
t
u
r
e
0
=
h
t
e
x
t
u
r
e
0
=
2
L
w_{texture0}=h_{texture0}=2^L
wtexture0=htexture0=2L
下一层
w
t
e
x
t
u
r
e
1
=
h
t
e
x
t
u
r
e
1
=
2
L
−
1
w_{texture1}=h_{texture1}=2^{L-1}
wtexture1=htexture1=2L−1
采样
i
m
a
g
e
1
(
i
,
j
)
=
I
0
(
2
i
,
2
j
)
+
I
0
(
2
i
+
1
,
2
j
)
+
I
0
(
2
i
,
2
j
+
1
)
+
I
0
(
2
i
+
1
,
2
j
+
1
)
4
image_1(i,j)=\dfrac{I_0(2i,2j)+I_0(2i+1,2j)+I_0(2i,2j+1)+I_0(2i+1,2j+1)}{4}
image1(i,j)=4I0(2i,2j)+I0(2i+1,2j)+I0(2i,2j+1)+I0(2i+1,2j+1)
如何选择合适的一层?
∂
u
t
e
x
e
l
∂
x
s
c
r
e
e
n
\dfrac{\partial u_{texel}}{\partial x_{screen}}
∂xscreen∂utexel水平方向上每像素 纹素的变换
∂
u
t
e
x
e
l
∂
y
s
c
r
e
e
n
\dfrac{\partial u_{texel}}{\partial y_{screen}}
∂yscreen∂utexel垂直方向上每像素 纹素的变换
如果像素和纹素一一对应,一个近似的方法
(
∂
u
t
e
x
e
l
∂
x
s
c
r
e
e
n
)
2
+
(
∂
v
t
e
x
e
l
∂
x
s
c
r
e
e
n
)
2
=
1
(\dfrac{\partial u_{texel}}{\partial x_{screen}})^2+ (\dfrac{\partial v_{texel}}{\partial x_{screen}})^2=1
(∂xscreen∂utexel)2+(∂xscreen∂vtexel)2=1
(
∂
u
t
e
x
e
l
∂
y
s
c
r
e
e
n
)
2
+
(
∂
v
t
e
x
e
l
∂
y
s
c
r
e
e
n
)
2
=
1
(\dfrac{\partial u_{texel}}{\partial y_{screen}})^2+ (\dfrac{\partial v_{texel}}{\partial y_{screen}})^2=1
(∂yscreen∂utexel)2+(∂yscreen∂vtexel)2=1
假设取max那方向
s
i
z
e
=
m
a
x
(
(
∂
u
t
e
x
e
l
∂
x
s
c
r
e
e
n
)
2
+
(
∂
v
t
e
x
e
l
∂
x
s
c
r
e
e
n
)
2
,
(
∂
u
t
e
x
e
l
∂
y
s
c
r
e
e
n
)
2
+
(
∂
v
t
e
x
e
l
∂
y
s
c
r
e
e
n
)
2
)
size=max(\sqrt{(\dfrac{\partial u_{texel}}{\partial x_{screen}})^2+ (\dfrac{\partial v_{texel}}{\partial x_{screen}})^2},\sqrt{(\dfrac{\partial u_{texel}}{\partial y_{screen}})^2+ (\dfrac{\partial v_{texel}}{\partial y_{screen}})^2})
size=max((∂xscreen∂utexel)2+(∂xscreen∂vtexel)2,(∂yscreen∂utexel)2+(∂yscreen∂vtexel)2)
s
i
z
e
2
L
=
1
→
L
=
log
(
s
i
z
e
)
log
2
\dfrac{size}{2^L}=1\to L=\dfrac{\log(size)}{\log{2}}
2Lsize=1→L=log2log(size)
作业
已知屏幕坐标系(1200600),在片元中的三个点(属性分别为 x , y , z n d c , u , v ) x,y,z_{ndc},u,v) x,y,zndc,u,v)转换到屏幕坐标系中为A(100,100,1/2,0,0),B(200,100,1/3,0,1),C(100,200,1/4,1,0),采用邻近采样,纹理图像为灰度图像,大小为5050,第0行纹理值全为0,第1行为1,…,第49行为49。求屏幕中(100,150)(即AC中点)的像素值。



























 1121
1121

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








