理解Jacobian矩阵与分布变换

理解Jacobian矩阵

本文主要是以下教程的一个整理：
Khan-academy: The Jacobian matrix
可能有错，欢迎指正。

Locally Linear

我们考虑一下简单的函数：
$$f\left(\left[\begin{array}{l}x\\ y\end{array}\right]\right)=\left[\begin{array}{l}x+\sin (y)\\ y+\sin (x)\end{array}\right]$$
他将一个[x,y]的点，经过一个变换，就像下图那样：

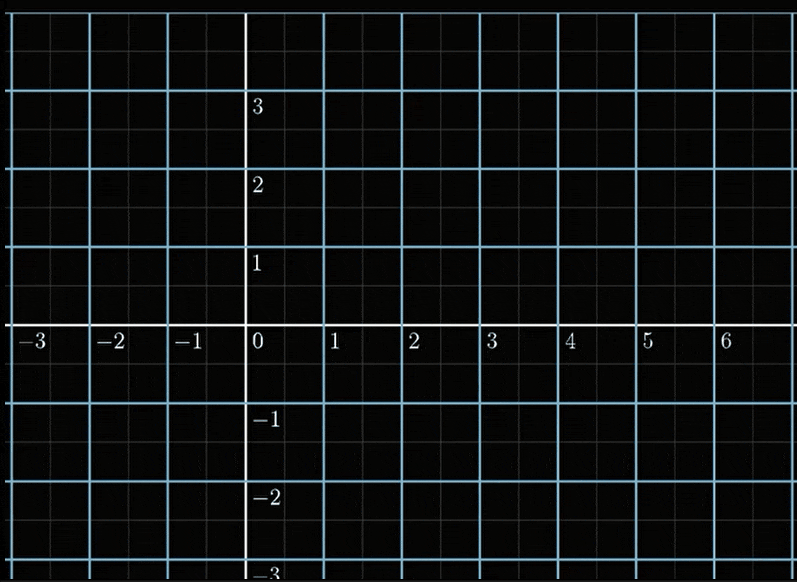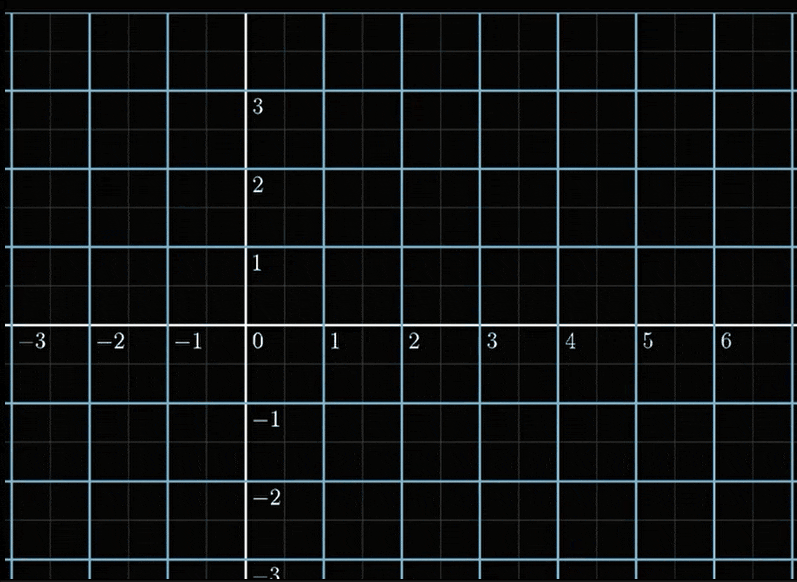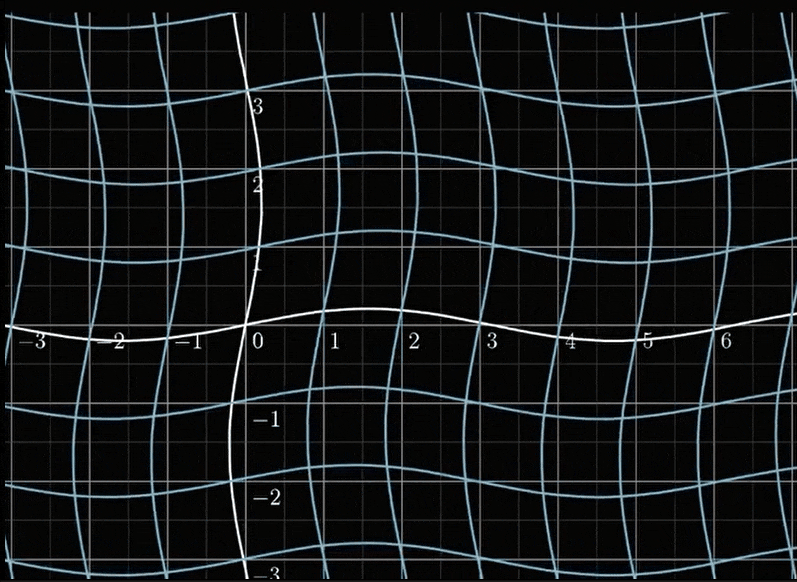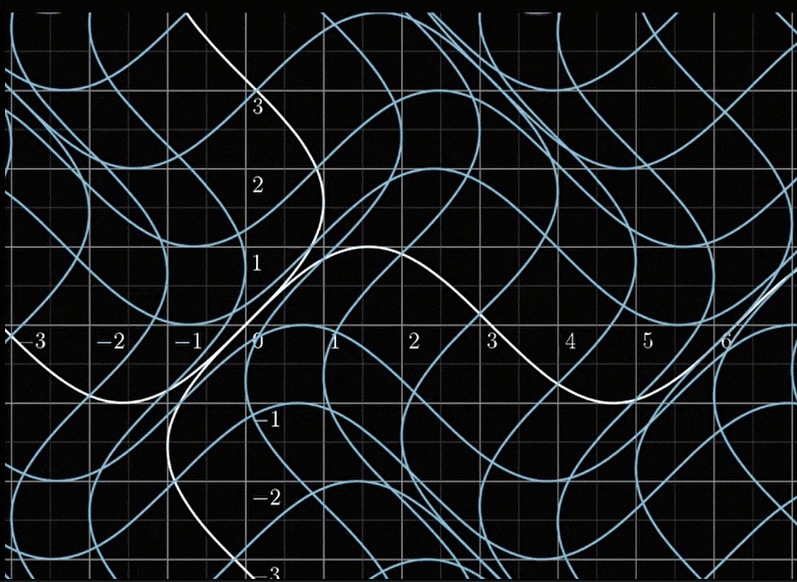
这似乎很复杂，没办法分析，但一个很重要的性质是Localy linear, 我们看一个很小的正方形：

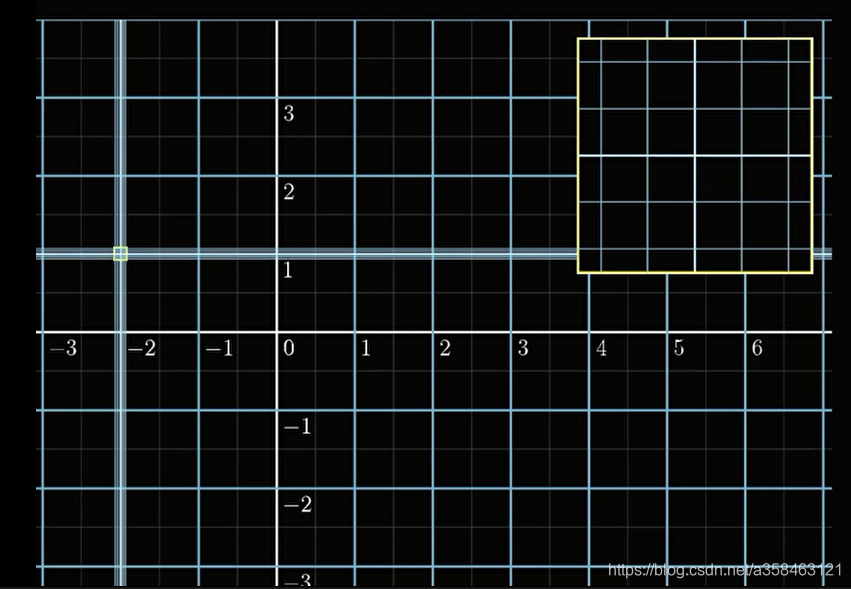
然后进行上述变换的操作：

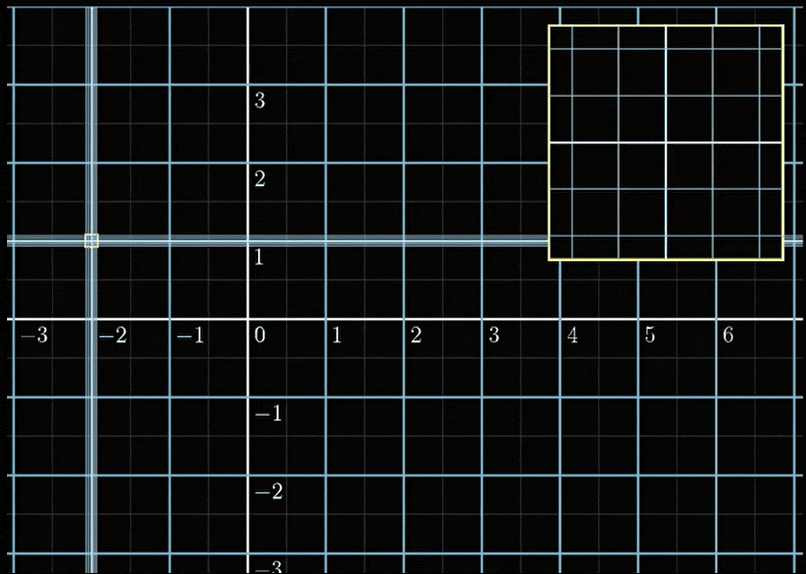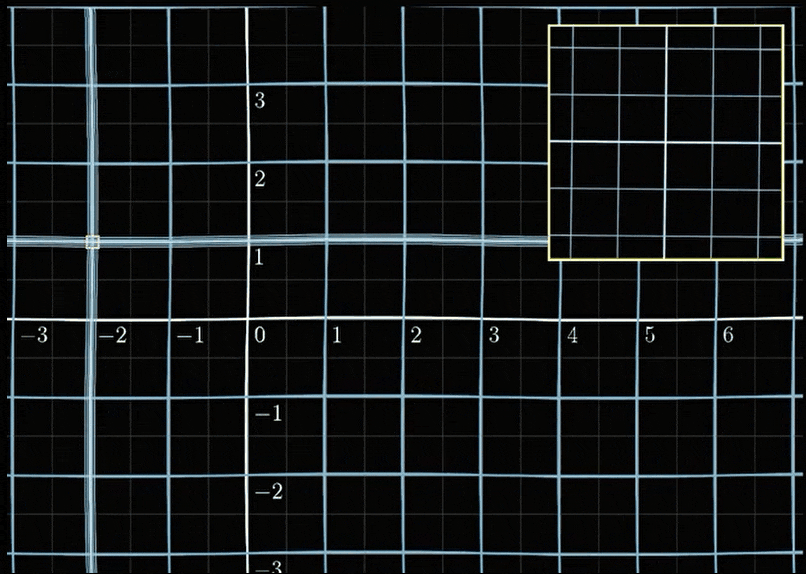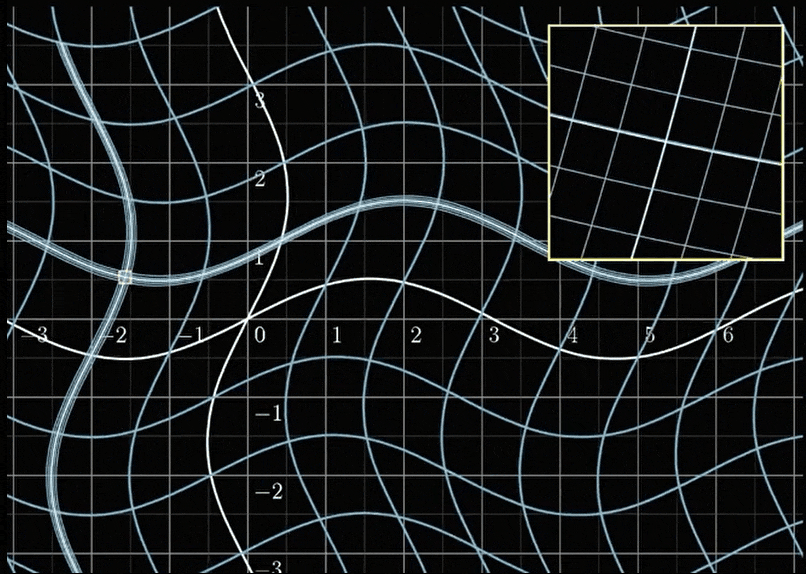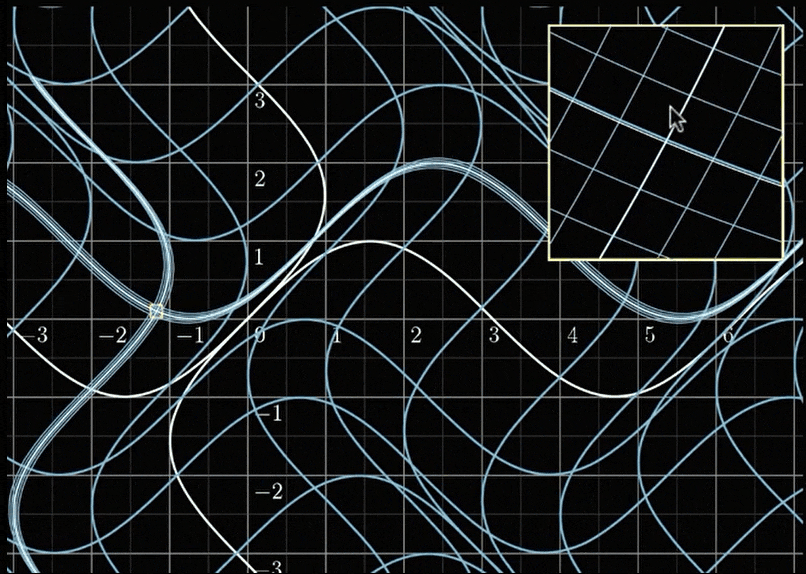
神奇的事情发生了，在局部结构里面，这个变换看起来就是一个线性变换。等等，线性变换是什么意思？

线性变换

线性变换是什么意思？我们知道，一个向量乘一个矩阵其实就是一个线性变换，但直观来看，是什么样的，我们看以下这个线性变换是怎样的。

$$\left[\begin{array}{rr}2& -3\\ 1& 1\end{array}\right]\left[\begin{array}{l}x\\ y\end{array}\right]\to \left[\begin{array}{ll}2x+(-3)& y\\ 1x+1& y\end{array}\right]$$

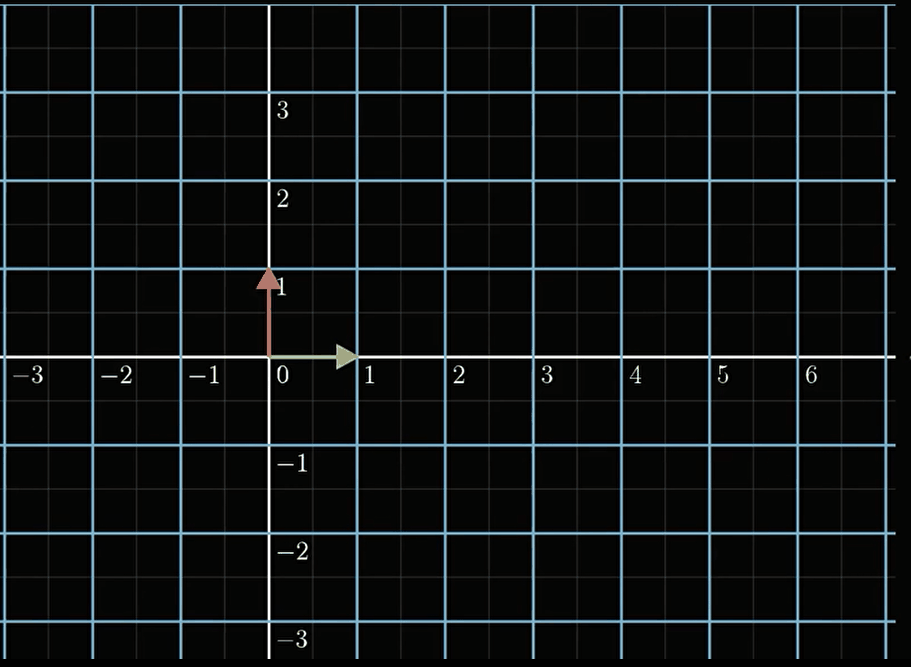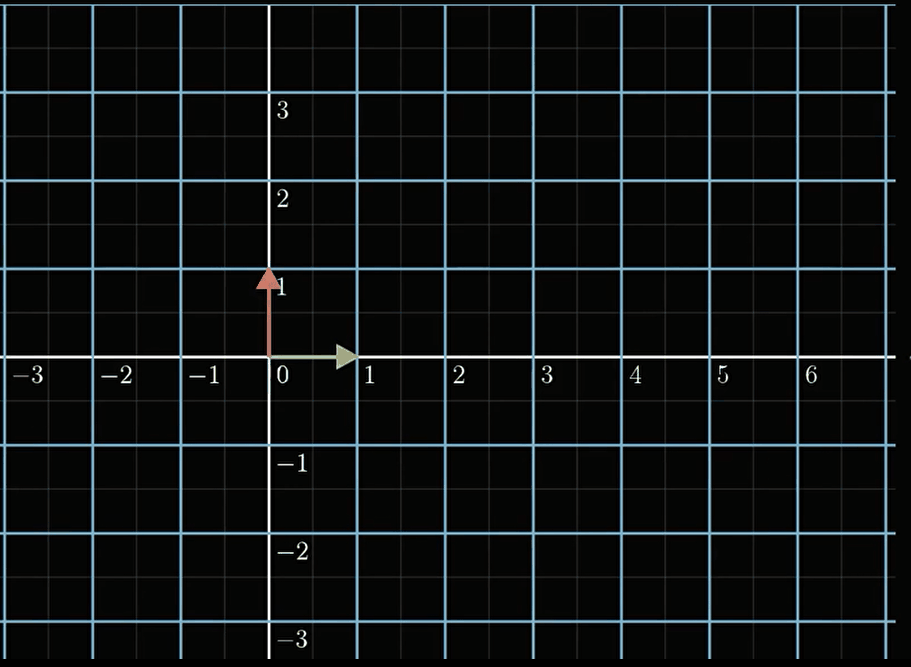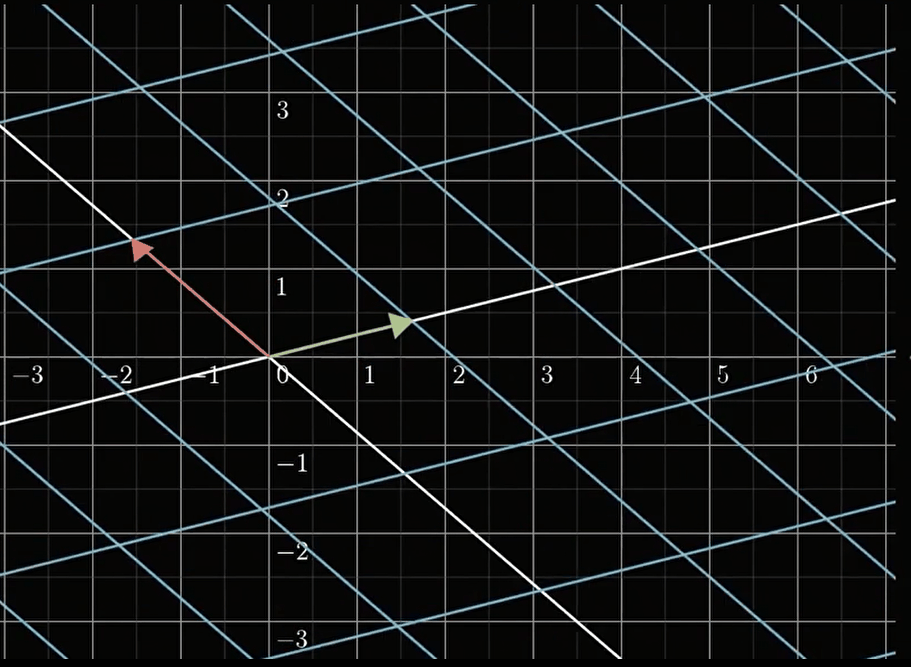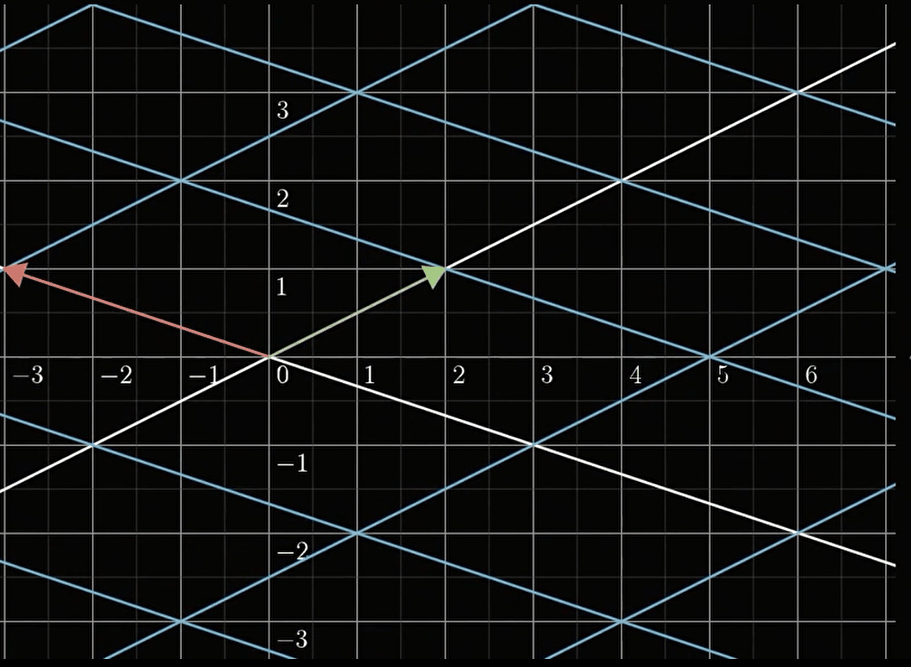
可以看到，对比于非线性变换，线性变换之后的坐标，其实都是相互平行的，换句话说，如果我们能知道基在线性变换后的结果，我们就能想象出整个坐标系是长什么样的。显然，

$$\left[\begin{array}{rr}2& -3\\ 1& 1\end{array}\right]\left[\begin{array}{l}1\\ 0\end{array}\right]\to \left[\begin{array}{l}2\\ 1\end{array}\right]$$

$$\left[\begin{array}{rr}2& -3\\ 1& 1\end{array}\right]\left[\begin{array}{l}0\\ 1\end{array}\right]\to \left[\begin{array}{l}-3\\ 1\end{array}\right]$$

我们发现，基变换后的结果恰好对应与变换矩阵的第一列和第二列！

Jacobian Matrix

现在回到正题，我们刚才说了，非线性的变换在某个局部点上的变换，可以看作是一个线性变换，而这个线性变换应该是一个2*2的矩阵来的，我们希望知道这个矩阵是什么。

现在我们开始分析一下这个局部变换：先考虑在原空间上x轴一个很小的距离dx:

经过一个线性变化，这个很短的$\partial x$变成了在另一个空间中很小的一步（如下图绿色箭头）

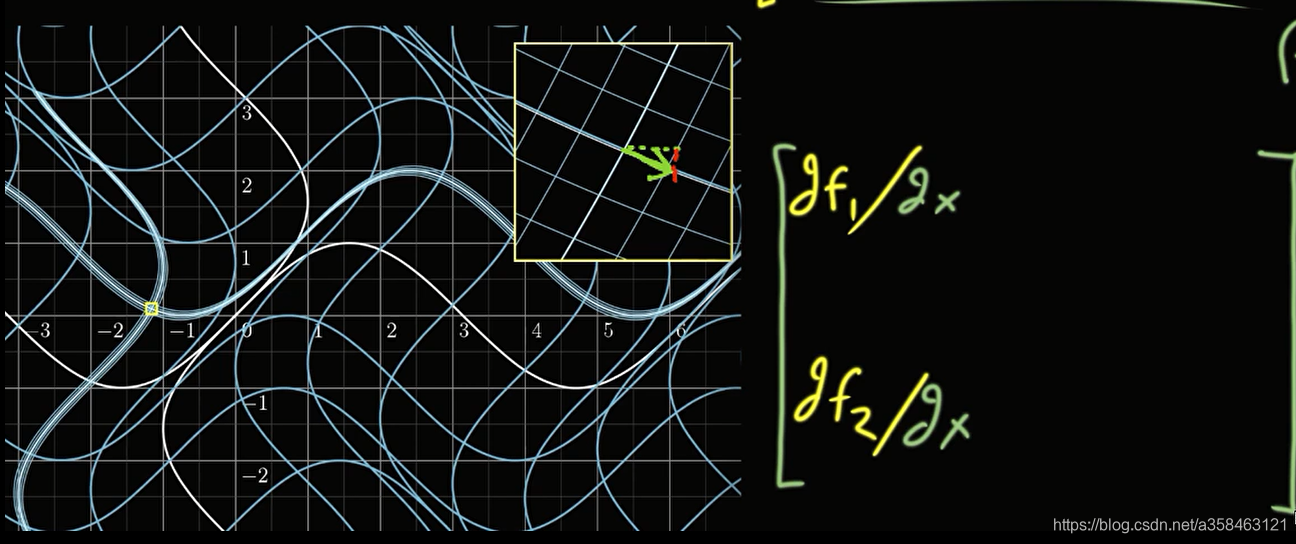
这个绿色的箭头，就是$\partial x$经过变换后的样子，可以看到这个变换是斜向下的变换，也就是说他同时改变了两个坐标，是一种2维的变换，该变换可以分解成两个坐标上的变换，在x轴上的变换后的长度就是绿色虚线，这个长度是等于$\partial f_1=\partial f_1/\partial x\ast \partial x$，而变换率则是$\partial f_1/\partial x$ (ps: 之所以可以用导数表示变化率是因为这就是导数的定义：${\lim }_{\Delta x\to 0}\frac{f(x+\Delta x,y)-f(x,y)}{\Delta x}$)，同理，在y轴上的变换是红色虚线，$\partial f_2/\partial x$.

回想一下，根据上面的线性变换矩阵，我们知道，变换矩阵的第一列实际上是用来变换x轴的值，所以我们将$\partial f_1/\partial x$和$\partial f_2/\partial x$.放在变换矩阵的第一列，同理

原始坐标的$\partial y$，经过变换后（红色箭头）的坐标，在新坐标系上的变化率是$\partial f_1/\partial y$和$\partial f_2/\partial y$. 于是我们就得到了jacobian matrix，他可以实现线性转换：

$$\left[\begin{array}{rr}\partial f_1/\partial x& \partial f_1/\partial y\\ \partial f_2/\partial x& \partial f_2/\partial y\end{array}\right]\left[\begin{array}{l}\partial x\\ 0\end{array}\right]\to \left[\begin{array}{l}\partial f_1\\ \partial f_2\end{array}\right]$$

$$\left[\begin{array}{rr}\partial f_1/\partial x& \partial f_1/\partial y\\ \partial f_2/\partial x& \partial f_2/\partial y\end{array}\right]\left[\begin{array}{l}0\\ \partial y\end{array}\right]\to \left[\begin{array}{l}\partial f_1\\ \partial f_2\end{array}\right]$$

理解分布变换

现在我们思考下概率分布变换的问题，考虑如下变换：
$$\mathbf{y}=g(\mathbf{x})$$

随机变量通过一个函数f进行变换，根据公式，他们的分布变换公式为：

$$\begin{gathered} p_x(x)=p_y(g(x))\ast |\det Jg(x)| \\ {p}_y(y)=p_x(g^{-1}(y))\ast |\det J{g}^{-1}(y)| \end{gathered}$$

其实出现这个原因是因为我们希望这个通过变换后的分布的积分${\int }_x{p}_y(g(x))dx$是等于1的，然而，如果g是非线性变换，其映射空间的dy与原空间dx的长度是不相等的（如果x是高维就是dx的体积不再相等），从而导致这个积分是不等于1的。为了修复这个积分，我们需要将dx转换，使得他适用于另外一个空间：$|\det Jg(x)|\ast dx$，这个转换就是乘上Jacobian matrix, 从上一章内容我们知道，乘上一个Jacobian可以将dx的长度转换成dy的长度，又因为，我们知道$p_y$对于$dy$的积分是等于1的，所以转换后对于dx的积分也是等于1的.

我们可以进一步直观地来理解这个分布变换：

如图所示，这是一个p(x)到p(y)分布转换的一个例子，我们发现，在x被拉长了两倍，于是，如果我们不做任何补偿，将会出现$p_y(y)=p_x(\frac{y-1}{2})=1$的情况，显然，这时候新的分布$p_y(y)$的面积是等于2的，这显然是错的。这是因为$dx=\frac{1}{2}dy$，要想在dy的积分下等于1，那么就要补偿从dx转到dy这一尺度转换的损失：

$$p_y(y)=p_x(\frac{y-1}{2})\frac{1}{2}=0.5$$

这里1/2其实就是等于$(\frac{y-1}{2}{)}^{\prime }=1/2$

参考资料

https://www.khanacademy.org/math/multivariable-calculus/multivariable-derivatives/jacobian/v/the-jacobian-matrix