#介绍
对于处理现实中的数据时,我们常常会遇到缺失值,这里我们将介绍一种缺失值的填补方法missForest,这是利用随机森林来填补缺失值的非参数方法,他可以适用于任何类型的数据(连续、离散)。其他类似的缺失值填补方法还有MICE,在这里不做介绍。
#方法
我们假设我们的数据是
X
=
(
X
1
,
X
2
,
.
.
.
,
X
p
)
X=(X_1,X_2,...,X_p)
X=(X1,X2,...,Xp)的n*p的一个矩阵。如果对于一个任意的变量
X
s
X_s
Xs,我们想填充他的缺失值,我们可以将数据分成4部分:
1.用
y
o
b
s
(
s
)
y^{(s)}_{obs}
yobs(s)表示
X
s
X_s
Xs的观测值。
2.用
y
m
i
s
(
s
)
y^{(s)}_{mis}
ymis(s)表示
X
s
X_s
Xs的缺失值。
3.用
x
o
b
s
(
s
)
x^{(s)}_{obs}
xobs(s)表示
X
s
X_s
Xs以外的观测值。
4.用
x
m
i
s
(
s
)
x^{(s)}_{mis}
xmis(s)表示
X
s
X_s
Xs的缺失值以外的其余观测值。
我画了一个图,可以帮助大家更好的理解这4个部分的组成:
红色部分就是
y
o
b
s
(
s
)
y^{(s)}_{obs}
yobs(s),黄色部分是
y
m
i
s
(
s
)
y^{(s)}_{mis}
ymis(s),绿色部分是
x
o
b
s
(
s
)
x^{(s)}_{obs}
xobs(s),蓝色部分是
x
m
i
s
(
s
)
x^{(s)}_{mis}
xmis(s)。
接来下我们只需要使用随机森林,训练出y~x的模型,然后将缺失值预测出来就可以了,但是不只是Xs存在缺失值,其他变量也是有可能存在缺失值的,这时候我们可以通过迭代的方式来求解。
我们先对缺失值做一个初始的猜测,比如用均值/中位数填充,然后按照变量的缺失率,从小到大排序,先对缺失率小的变量使用随机森林回归从而填补该变量的缺失值,然后一直迭代,直到最新的一次填补结果与上一次的填补结果不再变化(变化很小)时停止。
具体伪代码在这里:
这里的收敛指标是迭代中缺失值变化的大小,对于连续型变量,我们有:
对于离散型变量:
其中#NA是在离散变量中的总的缺失值数量。
#R语言实现应用
我们可以使用R包:missForest 来应用这一方法:
以下是一个使用例子:
> library(missForest)
> set.seed(81)
> iris.mis <- prodNA(iris, noNA = 0.2) #产生20%缺失值
> summary(iris.mis)
Sepal.Length Sepal.Width Petal.Length Petal.Width Species
Min. :4.300 Min. :2.000 Min. :1.100 Min. :0.100 setosa :40
1st Qu.:5.200 1st Qu.:2.800 1st Qu.:1.600 1st Qu.:0.300 versicolor:38
Median :5.800 Median :3.000 Median :4.450 Median :1.300 virginica :44
Mean :5.878 Mean :3.062 Mean :3.905 Mean :1.222 NAs :28
3rd Qu.:6.475 3rd Qu.:3.300 3rd Qu.:5.100 3rd Qu.:1.900
Max. :7.900 Max. :4.400 Max. :6.900 Max. :2.500
NAs :28 NAs :29 NAs :32 NAs :33
> iris.imp <- missForest(iris.mis, verbose = TRUE)
> iris.imp$ximp #修补后的数据
> head((iris.imp$ximp-iris)[,1:4])
Sepal.Length Sepal.Width Petal.Length Petal.Width
1 0.00000000 0.00000 0.00000000 0.00000000
2 0.00000000 0.30825 0.00000000 0.02720000
3 0.00000000 0.00000 0.00000000 0.00000000
4 0.00000000 0.22050 -0.03142857 0.00000000
5 0.00000000 0.00000 0.00000000 0.00000000
6 0.01766667 0.00000 0.00000000 -0.02533333
可以看到修补的数据与原数据想减,我们就可以清楚的看到这个效果是很不错的,如果我们仅仅使用均值这样的填充方法,就不能够这么准确了。
当然这方法虽然效果比较好,但是相比均值填充的方法来讲,效率就太低了,如果数据量比较大的话,这个方法会很慢,至于如何使用,就看各位自己的取舍了。
#参考文献:
Stekhoven D J, Bühlmann P. MissForest–non-parametric missing value imputation for mixed-type data.[J]. Bioinformatics, 2012, 28(1):112-8.
作为分享主义者(sharism),本人所有互联网发布的图文均遵从CC版权,转载请保留作者信息并注明作者a358463121专栏:http://blog.csdn.net/a358463121,如果涉及源代码请注明GitHub地址:https://github.com/358463121/。商业使用请联系作者。












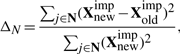
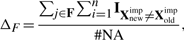
















 6359
6359

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








