树模型(一)：预备知识

1 信息论

1.1 信息

能消除不确定性的内容才能叫信息，而告诉你一个想都不用想的事实，那不叫信息。

比如数据分析师的工作经常是要用数据中发现信息，有一天上班你告诉老大从数据中发现我们的用户性别有男有女。。。（这不废话吗？）这不叫信息，但是如果你告诉老大女性用户的登录频次、加购率，浏览商品数量远高于男性，且年龄段在25岁~30岁的女性用户消费金额最多，15-20岁最少，那么我相信你老大会眼前一亮的！！！

如何衡量信息量？1948年有一位科学家香农从引入热力学中的熵概念，得到了信息量的数据公式：

$$y=-lo{g}_2{P}_k$$

$P_k$代表信息发生的可能性，发生的可能性越大，概率越大，则信息越少，通常将这种可能性叫为不确定性，越有可能则越能确定则信息越少；比如中国与西班牙踢足球，中国获胜的信息量要远大于西班牙胜利（因为这可能性实在太低~~）

1.2 信息熵

信息熵则是在信息的基础上，将有可能产生的信息定义为一个随机变量，那么变量的期望就是信息熵，比如上述例子中变量是赢家，有两个取值，中国或西班牙，两个都有自己的信息，再分别乘以概率再求和，就得到了这件事情的信息熵，公式如下：

$$H(D)=-\sum _{k=1}^K\frac{|D_k|}{|D|}lo{g}_2\frac{|D_k|}{|D|}$$

假如只有2个取值，曲线长得特别像金拱门，当Pk=0或1时，信息量为0，当Pk=0.5时，信息熵最大，想想看一件事情有N多种结果，有各种结果都同样有可能的时候，是不是最难以料到结局？

1.3 信息增益

信息增益是决策树中ID3算法中用来进行特征选择的方法，就是用整体的信息熵减掉以按某一特征分裂后的条件熵，结果越大，说明这个特征越能消除不确定性，最极端的情况，按这个特征分裂后信息增益与信息熵一模一样，那说明这个特征就能获得唯一的结果了。
这里补充一个概念：条件熵，公式为：

$$H(D|A)=-\sum _{i=1}^N\frac{|D_i|}{|D|}H(D_i)=-\sum _{i=1}^N\frac{|D_i|}{|D|}\sum _{k=1}^K\frac{|D_{ik}|}{|D_i|}lo{g}_2\frac{|D_{ik}|}{|D_i|}$$

信息增益为：

$$Gain(D,A)=H(D)-H(D|A)$$

1.4 信息增益率

信息增益率是在信息增益的基础上，增加了一个关于选取的特征包含的类别的惩罚项，这主要是考虑到如果纯看信息增益，会导致包含类别越多的特征的信息增益越大，极端一点，有多少个样本，这个特征就有多少个类别，那么就会导致决策树非常浅。公式为：
$$S=-\sum _{i=1}^K\frac{|D_i|}{|D|}lo{g}_2\frac{|D_i|}{|D|}$$
$$Gainratio(D,A)=\frac{H(D)-H(D|A)}{S}$$

1.5 基尼系数

基尼系数也是一种衡量信息不确定性的方法，与信息熵计算出来的结果差距很小，基本可以忽略，但是基尼系数要计算快得多，因为没有对数。
分类问题中，假设有K个类，样本点属于第K类的概率为$p_k$，则概率分布的基尼指数定义为

$$Gini(p)=\sum _{k=1}^K{p}_k(1-p_k)$$

对于二分类问题来说，若样本点属于第一类的·概率为p，则概率分布的基尼指数为

$$Gini(p)=2p(1-p)$$

对于给定的样本集合D，其基尼指数为

$$Gini(D)=1-\sum _{i=1}^K{\left(\frac{|D_i|}{|D|}\right)}^2$$

如果样本集合D根据特征A是否取某一可能的值α被分割成$D_1$和$D_2$，那么在特征A的条件下集合D的基尼指数为

$$Gini(D,A)=\frac{D_1}{D}Gini(D_1)+\frac{D_2}{D}Gini(D_2)$$

与信息熵一样，当类别概率趋于平均时，基尼系数越大

2 模型泛化

2.1 期望

期望是针对于随机变量而言的一个量，可以理解是一种站在“上帝视角”的值。针对于他的样本空间而言的。

均值是一个统计量(对观察样本的统计)，期望是一种概率论概念，是一个数学特征。

首先给出定义公式

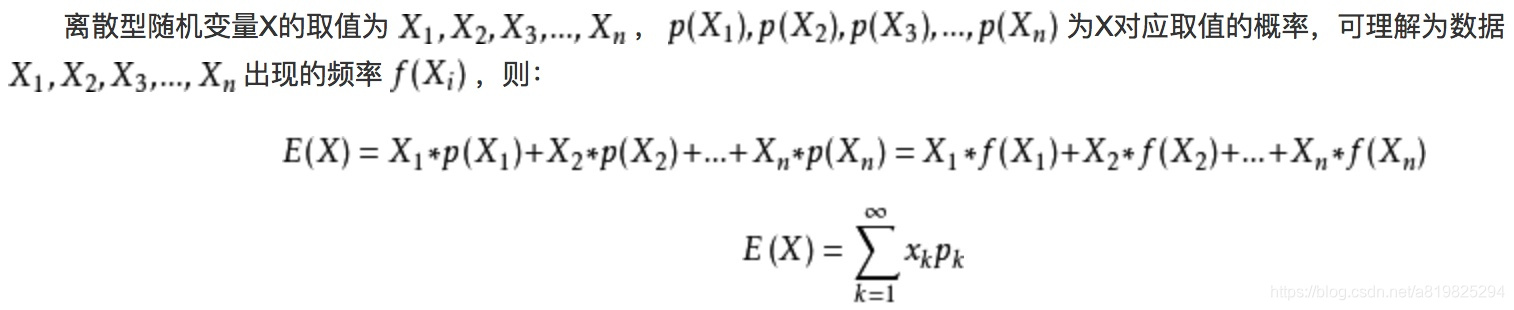
那么掷骰子例子对应的期望求法如下：

可以看出期望是与概率值联系在一起的，如果说概率是频率随样本趋于无穷的极限 ，期望就是平均数随样本趋于无穷的极限，可以看出均值和期望的联系也是大数定理联系起来的。

2.2 方差、偏差的由来

对学习算法除了通过实验估计其泛化性能之外，人们往往还希望了解它为什么具有这样的性能。**“偏差-方差分解”（bias-variance decomposition）**就是从偏差和方差的角度来解释学习算法泛化性能的一种重要工具。

在机器学习中，我们用训练数据集去训练一个模型，通常的做法是定义一个误差函数，通过将这个误差的最小化过程，来提高模型的性能。然而我们学习一个模型的目的是为了解决训练数据集这个领域中的一般化问题，单纯地将训练数据集的损失最小化，并不能保证在解决更一般的问题时模型仍然是最优，甚至不能保证模型是可用的。这个训练数据集的损失与一般化的数据集的损失之间的差异就叫做泛化误差（generalization error）。

而泛化误差可以分解为偏差（Biase）、方差（Variance）和噪声（Noise）。

2.3 简述偏差、方差、噪声

如果我们能够获得所有可能的数据集合，并在这个数据集合上将损失最小化，那么学习得到的模型就可以称之为**“真实模型”**。当然，在现实生活中我们不可能获取并训练所有可能的数据，所以“真实模型”肯定存在，但是无法获得。我们的最终目的是学习一个模型使其更加接近这个真实模型。

Bias和Variance分别从两个方面来描述我们学习到的模型与真实模型之间的差距。

• Bias是用所有可能的训练数据集训练出的所有模型的输出的平均值与真实模型的输出值之间的差异
• Variance是不同的训练数据集训练出的模型输出值之间的差异。
• 噪声的存在是学习算法所无法解决的问题，数据的质量决定了学习的上限。假设在数据已经给定的情况下，此时上限已定，我们要做的就是尽可能的接近这个上限。

2.4 公式定义偏差、方差、噪声

以回归任务为例，学习算法的期望预测为：

$$\hat{f}(x)=E_D(f(x;D))$$

这里的期望预测也就是针对不同数据集D，模型f对样本x的预测值取其期望，也叫做平均预测（average predicted）

（1）方差定义：
使用样本数相同的不同训练集产生的方差为：

$$var(x)=E_D[(f(x;D)-\hat{f}(x){)}^2]$$

方差的含义：方差度量了同样大小的训练集的变动所导致的学习性能的变化，即刻画了数据扰动所造成的影响

（2）偏差定义：
期望输出与真实标记的差别称为偏差（bias），即：

$$bia{s}^2(x)=(\hat{f}(x)-y{)}^2$$

偏差的含义：偏差度量了学习算法的期望预测与真实结果的偏离程度，即刻画了学习算法本身的拟合能力

（3）噪声：
噪声为：

$${\epsilon }^2=E_D[(y_D-y{)}^2]$$

噪声的含义：噪声则表达了在当前任务上任何学习算法所能达到的期望泛化误差的下界，即刻画了学习问题本身的难度

2.5 泛化误差与偏差、方差的关系

$$泛化误差=错误率(error)=bia{s}^2(x)+var(x)+{\epsilon }^2$$

也就是说，泛化误差可以通过一系列公式分解运算证明：泛化误差为偏差、方差与噪声之和。证明过程如下：

为了便于讨论，我们假定噪声期望为零，即$E_D[y_D-y]=0$ 。通过简单的多项式展开合并，可对算法的期望泛化误差进行分解：

“偏差-方差分解”说明，泛化性能是由学习算法的能力、数据的充分性以及学习任务本身的难度所共同决定的。给定学习任务，为了取得好的泛化性能，则需使偏差较小，即能够充分拟合数据，并且使方差较小，即使得数据扰动产生的影响小。

2.6 基于图形理解

假设红色的靶心区域是学习算法完美的正确预测值，蓝色点为训练数据集所训练出的模型对样本的预测值，当我们从靶心逐渐往外移动时，预测效果逐渐变差。

从上面的图片中很容易可以看到，左边一列的蓝色点比较集中，右边一列的蓝色点比较分散，它们描述的是方差的两种情况。比较集中的属于方差比较小，比较分散的属于方差比较大的情况。

我们再从蓝色点与红色靶心区域的位置关系来看，靠近红色靶心的属于偏差较小的情况，远离靶心的属于偏差较大的情况。

模型的偏差与方差

• **偏差：**描述样本拟合出的模型的预测结果的期望与样本真实结果的差距，要想偏差表现的好，就需要复杂化模型，增加模型的参数，但这样容易过拟合，过拟合对应上图的 High Variance，点会很分散。低偏差对应的点都打在靶心附近，所以喵的很准，但不一定很稳；
• **方差：**描述样本上训练出来的模型在测试集上的表现，要想方差表现的好，需要简化模型，减少模型的复杂度，但这样容易欠拟合，欠拟合对应上图 High Bias，点偏离中心。低方差对应就是点都打的很集中，但不一定是靶心附近，手很稳，但不一定瞄的准。

思考： 从上面的图中可以看出，模型不稳定时会出现偏差小、方差大的情况，那么偏差和方差作为两种度量方式有什么区别呢？
解答： Bias的对象是单个模型，是期望输出与真实标记的差别。它描述了模型对本训练集的拟合程度。

Variance的对象是多个模型，是相同分布的不同数据集训练出模型的输出值之间的差异。它刻画的是数据扰动对模型的影响

2.7 与K折交叉验证的关系

K-fold Cross Validation的思想：将原始数据分成K组(一般是均分)，将每个子集数据分别做一次验证集，其余的K-1组子集数据作为训练集，这样会得到K个模型，用这K个模型最终的验证集的分类准确率的平均数作为此K-CV下分类器的性能指标。

对于一系列模型$F(\hat{f},\theta )$, 我们使用Cross Validation的目的是获得预测误差的无偏估计量CV，从而可以用来选择一个最优的Theta*,使得CV最小。假设K-folds cross validation，CV统计量定义为每个子集中误差的平均值，而K的大小和CV平均值的bias和variance是有关的：

$$CV=\frac{1}{K}\sum _{k=1}^K\frac{1}{m}\sum _{i=1}^m(\widehat{f^k}-y_i{)}^2$$

其中，m = N/K 代表每个子集的大小， N是总的训练样本量，K是子集的数目。

当K较大时，m较小，模型建立在较大的N-m上，经过更多次数的平均可以学习得到更符合真实数据分布的模型，Bias就小了，但是这样一来模型就更加拟合训练数据集，再去测试集上预测的时候预测误差的期望值就变大了，从而Variance就大了；k较小的时候，模型不会过度拟合训练数据，从而Bias较大，但是正因为没有过度拟合训练数据，Variance也较小。