CUDA系列学习（五）GPU基础算法: Reduce, Scan, Histogram

喵~不知不觉到了CUDA系列学习第五讲，前几讲中我们主要介绍了基础GPU中的软硬件结构，内存管理，task类型等；这一讲中我们将介绍3个基础的GPU算法：reduce，scan，histogram，它们在并行算法中非常常用，我们在本文中分别就其功能用处，串行与并行实现进行阐述。
———-

1. Task complexity

task complexity包括step complexity（可以并行成几个操作） & work complexity（总共有多少个工作要做）。
e.g. 下面的tree-structure图中每个节点表示一个操作数，每条边表示一个操作，同层edge表示相同操作，问该图表示的task的step complexity & work complexity分别是多少。

Ans:
step complexity: 3；
work complexity: 6。
下面会有更具体的例子。

---

2. Reduce

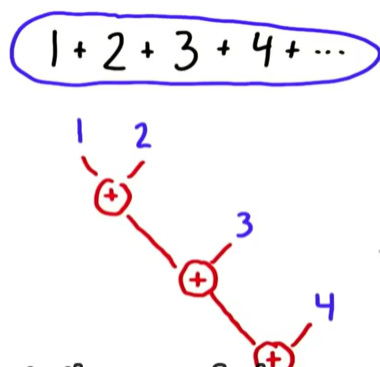
引入：我们考虑一个task：1+2+3+4+…
1) 最简单的顺序执行顺序组织为((1+2)+3)+4…
2) 由于operation之间没有依赖关系，我们可以用Reduce简化操作，它可以减少serial implementation的步数。

2.1 what is reduce?

Reduce input:

1. set of elements
2. reduction operation
   
   1. binary: 两个输入一个输出
   2. 操作满足结合律： (a@b)@c = a@(b@c), 其中@表示operator
      e.g +, 按位与 都符合；a^b(expotentiation)和减法都不是

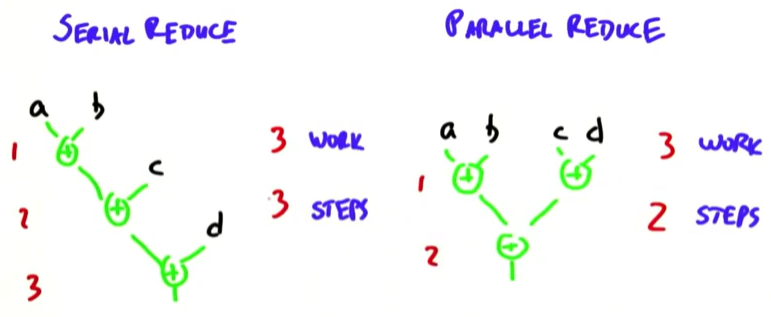
2.1.1 Serial implementation of Reduce:

reduce的每一步操作都依赖于其前一个操作的结果。比如对于前面那个例子，n个数相加，work complexity 和 step complexity都是O(n)（原因不言自明吧~）我们的目标就是并行化操作，降下来step complexity. e.g add serial reduce -> parallel reduce。

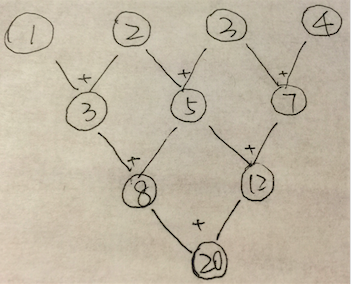
2.1.2 Parallel implementation of Reduce:

也就是说，我们把step complexity降到了$log_2n$

举个栗子，如下图所示：

那么如果对$2^{10}$个数做parallel reduce add，其step complexity就是10. 那么在这个parallel reduce的第一步，我们需要做512个加法，这对modern gpu不是啥大问题，但是如果我们要对$2^{20}$个数做加法呢？就需要考虑到gpu数量了，如果说gpu最多能并行做512个操作，我们就应将$2^{20}$个数分成1024*1024(共1024组)，每次做$2^{10}$个数的加法。这种考虑task规模和gpu数量关系的做法有个理论叫Brent’s Theory. 下面我们具体来看：

也就是进行两步操作，第一步分成1024个block，每个block做加法；第二步将这1024个结果再用1个1024个thread的block进行求和。kernel code：

__global__ void parallel_reduce_kernel(float *d_out, float* d_in){
    int myID = threadIdx.x + blockIdx.x * blockDim.x;
    int tid = threadIdx.x;

    //divide threads into two parts according to threadID, and add the right part to the left one, lead to reducing half elements, called an iteration; iterate until left only one element
    for(unsigned int s = blockDim.x / 2 ; s>0; s>>=1){
        if(tid<s){
            d_in[myID] += d_in[myID + s];
        }
        __syncthreads(); //ensure all adds at one iteration are done
    }
    if (tid == 0){
        d_out[blockIdx.x] = d_in[myId];
    }
}

Quiz: 看一下上面的code可以从哪里进行优化？

Ans：我们在上一讲中提到了global，shared & local memory的速度，那么这里对于global memory的操作可以更改为shared memory，从而进行提速：

__global__ void parallel_shared_reduce_kernel(float *d_out, float* d_in){
    int myID = threadIdx.x + blockIdx.x * blockDim.x;
    int tid = threadIdx.x;
    extern __shared__ float sdata[];
    sdata[tid] = d_in[myID];
    __syncthreads();

    //divide threads into two parts according to threadID, and add the right part to the left one, lead to reducing half elements, called an iteration; iterate until left only one element
    for(unsigned int s = blockDim.x / 2 ; s>0; s>>=1){
        if(tid<s){
            sdata[tid] += sdata[tid + s];
        }
        __syncthreads(); //ensure all adds at one iteration are done
    }
    if (tid == 0){
        d_out[blockIdx.x] = sdata[myId];
    }
}

优化的代码中还有一点要注意，就是声明的时候记得我们第三讲中说过的kernel通用表示形式：

kernel<<<grid of blocks, block of threads, shmem>>>

最后一项要在call kernel的时候声明好，即:

parallel_reduce_kernel<<<blocks, threads, threads*sizeof(float)>>>(data_out, data_in);

好，那么问题来了，对于这两个版本（parallel_reduce_kernel 和 parallel_shared_reduce_kernel）, parallel_reduce_kernel比parallel_shared_reduce_kernel多用了几倍的global memory带宽？ Ans: 分别考虑两个版本的读写操作：

parallel_reduce_kernel

Times	Read Ops	Write Ops
1	1024	512
2	512	256
3	256	128
…
n	1	1

parallel_shared_reduce_kernel

Times	Read Ops	Write Ops
1	1024	1

所以，parallel_reduce_kernel所需的带宽是parallel_shared_reduce_kernel的3倍。

---

3. Scan

3.1 what is scan?

• Example:

  • input: 1,2,3,4
  • operation: Add
  • ouput: 1,3,6,10（out[i]=sum(in[0:i])）

• 目的：解决难以并行的问题

拍拍脑袋想想上面这个问题O(n)的一个解法是out[i] = out[i-1] + in[i].下面我们来引入scan。

Inputs to