作者:i_dovelemon
来源:CSDN
日期:2014 / 9 / 28
主题:World Transform, View Transform , Projection Transform
引言
在3D图形学中,基本几何变换是一个非常重要的操作。可以说,整个3D图形能够有效的显示,就是由于几个非常重要的基础3D变换贡献的。在前面的文章中,向大家承诺了,要详细的讲解在3D图形学中的三个基本的坐标变换。今天,就来像大家讲述,DirectX是如何进行变换。
变换的目的
在我们讲解具体的变换工作之前,我们需要知道,为什么需要进行变换?在3D图形学中,有很多不同的坐标系统。比如说,模型坐标系统,世界坐标系统,视空间坐标系统,裁剪空间坐标系统等等。为什么需要如此之多的坐标系统了?那是因为,不同的工作,在不同的坐标系统中进行,会给我们的工作带来很多方便。比如说,我们定义模型的时候,在模型的坐标空间中定义,而不是在世界空间坐标系里面定义。在模型坐标里面,我们可以只关心模型的基本构造,它的外形等,不需要考虑它将来会放在场景中的哪个地方,面朝的方向是哪里。这样做就能够大大的减少我们的工作。所以,一句话,进行坐标变换的目的就是为了简化工作,让我们的工作更加容易的完成而已(虽然初学来说,好像没有简化我们的工作???)。
如何变换
在前面我写过一篇文章,3D图形变换。在这篇文章中,讲述了如何使用矩阵来进行同一个维度的坐标变换。不过,这里讲解的变换,只是对那些只需要进行平移,旋转的坐标系统来说的。对于要进行缩放的坐标变换,并不是使用这种方法。有时候,我们需要根据变换的各种条件,来推导出最终变换的矩阵。这种方法在那些变换后的矩阵很难用其他的坐标系统来描述它们的坐标基的时候使用。
DirectX变换流程
在DirectX中,有三种变换,是每一个3D应用程序,每一帧都会使用到的变换。它们分别是World Transform(世界坐标变换), View Transform(视空间坐标变换,又称相机坐标变换)和最麻烦的Perspective Projection Transform(透视投影变换,正交投影不是经常使用的变换,这里不介绍这种)。下面,我们来一一的介绍这些变换的作用,以及如何构建他们。
World Transform
世界坐标变换,顾名思义,是将模型坐标变换到世界空间中的变换。我们要知道,任何的变换都可以拆分称为平移,旋转,缩放,这三个大的变换方式。对于世界变换来说,我们完全可以按照3D图形变换中描述的那样来进行坐标的平移和旋转变换。如果需要将模型进行缩放的话,我们在构建一个缩放的矩阵(这个矩阵在任何3D书籍上都有介绍,这里不再赘述),然后把这个缩放矩阵,与前面的矩阵结合起来,就能够完成一个世界坐标变换的功能了。这是三个坐标变换里面最简单的变换。
View Transform
在3D空间中,我们会定义一个虚拟的实际上在3D空间中并没有用任何模型表示的相机。我们能够在程序界面上看到的内容,都是通过相机的位置,和属性等等来构建的。相机变换的作用是将原本相对于世界坐标中心的物体,变换到以相机为坐标中心的相机坐标空间中去。因为很多的处理,在世界坐标空间中进行比较麻烦,如物体剔除,背面消除等等。这些工作如果能够在相机坐标空间中进行的话,那么就会轻松很多。进行相机坐标变换我们需要定义相机的属性。在DirectX中使用的是一种称之为UVN的相机模型。我们定义了相机的三个坐标基向量Right,Up和Look向量在世界坐标系中的表示,以及相机在世界坐标空间的位置。这样,我们只要简单的使用3D图形变换里面介绍的方法,将这三个向量和位置属性构成如下的矩阵:
不过读者需要注意:这里的矩阵,是将相机空间里面的坐标变换到世界坐标空间中去的矩阵。我们需要的是相反效果的矩阵,那么我们只要求这个矩阵的逆矩阵就可以了。求逆的过程,在任何的线性代数书上都有,这里直接给出逆矩阵:
读者能够发现,这里的矩阵就是DirectX中使用的矩阵了。它的推导过程就是这么的简单。
Perspective Projection Transform
投影变换是这三个中最复杂的变换。在DirectX中,它的投影变换矩阵做了很多的事情。这也就导致了它的变换矩阵十分的复杂。所以,为了能够详细的掌握这个变换过程,我们先要弄清楚,进行这个变换的目的何在。
在DirectX中,投影变换的目的,是让3D的模型数据等变换称为2D的图像,从而显示在屏幕上,这个过程称之为投影。投影意味着,我们需要对模型的X和Y坐标进行一些变换,从而能够根据它在相机空间中的上下左右顺序,正确的绘制在屏幕上。同时,由于是3D空间,模型的图像之间存在这遮罩的关系,远的物体会被近的物体遮挡住,我们同样还需要保存一些信息,从而能够判断哪一个在前面,哪一个在后面,这个值自然就是Z值了。Z值越小,说明了它越靠近相机,那么它后面的物体就不应该被绘制,因为都被它挡住了。
我们把DirectX的投影变换分为两个部分,一个部分是真真的投影过程,将相机坐标空间里面的模型的X和Y坐标正确的投影到我们选定的一个平面上来。因为要最终构成一个2D的图像,所以很自然的想到将3D空间的物体坐标投影的一个平面上来。这个平面,在图形学上被称为投影面。投影面的选择是任意的,只要能够很方便的进行处理即可。在DirectX中选择近裁剪面为投影平面。但是,不同的程序,可能选择不同的尺寸作为程序的显示窗口。DirectX为了将这层关系忽略掉,它统一的将模型的X和Y坐标变换到[-1,1]这个范围来。这样,在最后只要根据屏幕的宽和高分别乘以这个变换后的值,就能够得到在屏幕上的坐标了(这个就是视口变化的原理)。同时,变换到[-1,1]这个范围,我们对模型进行3D裁剪时的操作也会变得十分的简单。
另外一个部分就是对遮罩关系的Z值进行保存的工作。我们需要将图像的先后关系保存起来。在上面讲解过进行投影过后,他们的点都在近裁剪面上了,那么他们的Z值将都是近裁剪面的Z值,也就是说Z值的遮罩信息丢弃了。所以,我们需要进行一些工作来将这个Z值信息保存下来。
好了,在知道了DirectX的透视投影变换做了哪些工作之后,我们来实际的进行矩阵的推导。
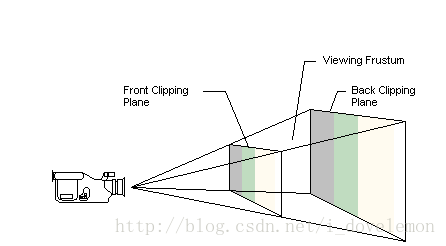
在推导之前,我们来看下相机所形成的视域体的结构:
这个结构体,是由近裁剪面(Front Clipping Plane) 和远裁剪面(Back Clipping Plane)截取相机的视野形成的椎体而得到的一个台体。这个台体里面的模型就是将要变换到投影平面上的模型。
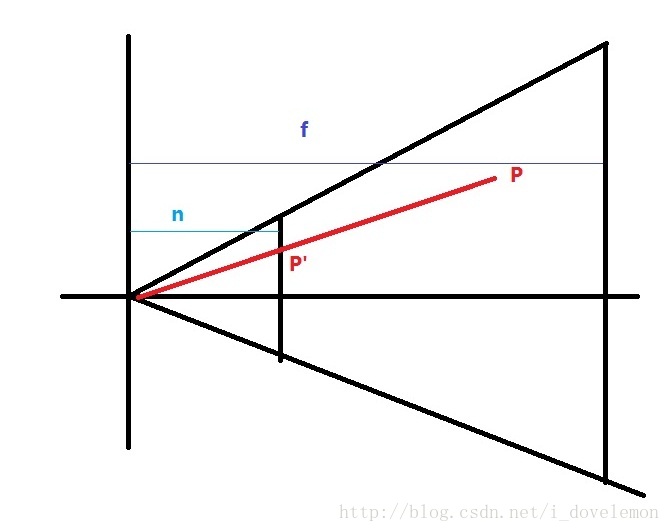
我们选取Y-Z平面来观察下投影过程,这个过程同样能够用在X-Z平面上:
从图中,我们可以看到在视域体里面的点P(px, py, pz)经过与相机的原点的连线与近平面的交点为P‘。P’即为投影过程得到的投影点。P‘的坐标很容易计算出来。只要利用相似三角形的原理,我们很容易的得出如下的结论:
P’.y / n = P.y / P.z == P'.y = P.y * n / P.z (1)
同理,我们对X-Z平面进行同样的操作,可以得到如下的结论:
P‘.x / n = P.x / P.z == P'.x = P.x * n / P.z (2)
即投影点的坐标为:
P' = (P.x * n / P.z , P.y * n / P.z, P.z) (3)
我们在上面讨论过,为了能够简单的进行3D裁剪,忽略尺寸的大小,我们需要将投影坐标变换到[-1,1]这个范围来。也就是说,我们还需要另外的处理,假设这个过程得到的点是P’‘。那么就有如下的结论:
P''.x / P'.x = 2 / W , P’‘.y / P'.y = 2 / H (4)
这个结论是因为变换后的X,Y的范围和原来的X,Y范围是线性变化的,所以我们可以利用同比的概念来进行比较,从而得到了在[-1,1]范围里面的X,Y坐标分别为:
P’‘.x = 2 * P'x / W , P''.y = 2 * P'.y / H (5) (其中W是投影平面的宽度,H是投影平面的高度)
将公式(3)中的数据带入公式(5),得到如下的结论:
P''.x = 2 * P.x * n / (P.z * W) , P''.y = 2 * P.y * n / (P.z * H) (6)
由于H,W分别是投影平面的高度和宽度(即最终屏幕的高度和宽度),所以得到如下的结论:
P’’.y = P.y / P.z * cot(a) (7) cot(a) = 2 * n / H , a为相机的上下视野角度的一半
在DirectX中,还传入了一个宽高比Aspect = W / H, 即得到 :
W = H * Aspect (8)
将公式(8)带入公式(6),得到P‘’.x:
P''.x = 2 * P.x * n / (P.z * H * Aspect) = (P.x / P.z ) * (cot(a) / Aspect) (9)
好了,第一部分的推导已经完毕了,我们已经知道了如何将模型的X,Y坐标变换到[-1,1]空间中去了。剩下的部分就是如何保存Z值了。
由于经过上面的变换之后,模型坐标的Z值都变成了近裁剪面的值n了,而我们需要的是Z值的先后关系。 我们发现这个关系就保存在原来未进行上面的变换的相机空间坐标的Z值中。也就是说,经过相机变换后的Z坐标已经能够很好的判断哪些点是在哪些点的后面了。我们可以将这个值保存下来。但是DirectX并没有这么做。那是因为,这个Z值可能很大,也可能很小。这就会导致Z缓存在设计上的困难。所以,使用对X,Y坐标同样的方法,不同的是这次变换到[0,1]范围来。读者看到这里可能想,那么就简单的使用如下的公式:
P‘’.z = (P''.z - n ) / (f - n) (10)
的确,上面的公式看起来似乎是正确的,和上面同样的使用同比的概念来进行。但是,如果读者这么认为就大错特错了。同比概念能够得出这样的结论的前提是Z值的变换是线性的。我们这里经过投影变换后的数据,将来都要在光栅化函数里面,通过在屏幕坐标空间线性插值来进行像素颜色的计算,填充,从而实现光栅化。对于X,Y来说,他们在屏幕空间依然是线性变换的。
但是对于Z坐标来说,我们并不希望它在屏幕空间中是线性变换的。想象一下,我们看到的一个物体,都是靠近我们的边缘比较清晰,远的边缘比较模糊。这显示在数据上就是近的边缘,它的纹理坐标的变化比较细微,比较缓慢,而远的变化比较大,比较迅速。这个概念,在图形学上称之为透视修正,是为了能够营造出真真意义上的透视感觉而提出的概念。
所以,DirectX也将这个概念加入进去了。虽然Z值并不是线性变换的,但是实现上面的透视效果的时候,1/z的值是呈线性变化的。也就是说,我们在进行光栅化处理的时候,可以对纹理坐标进行线性插值了。只要插值计算的时候使用的是1/z来进行的即可。这样,原本不是线性变换的纹理坐标,我们能够通过线性插值的方法来进行计算了。
说到这里,大家可能有点晕晕乎乎的了。总之一句话,为了能够让显示的图像效果上更加的真实,我们需要将1/z的信息保存起来,而不是Z的信息。
好了,也就是说,我们只要将原来的z值变成1/z,然后进行变换,到[0,1]空间中即可。
实际上,在这里,我们直接保存1/z作为新的Z值也就可以了,但是这样的话,我们在进行Z-Test的时候,就不是直观上的哪一个Z值小就靠前。读者想象看,如果Z值小的话,由于Z值是1/z'计算出来的,那么原来相机空间中的Z‘值就大的值,也就是说它反而是靠后的。
DirectX在这里有做了一层工作,它希望保留这种直观的印象,当Z值小的时候,就表示该像素是靠前的,Z值大的时候,就表示该像素靠后。
所以,DirectX在1/z的基础上,在进行了一次线性变换,由于线性变换并不改变值的线性变化属性,所以可以再次使用,虽然会改变值,但是我们并不是使用值来获取像素的精确位置,而是判断他们的先后关系,只要这样的关系不变,它的值是多少,一点关系都没有。
线性变化关系即是正比关系,我们可以用y = ax + b这样的一次函数来表示。
所以,DirectX希望满足如下的条件:
Z' = a * 1 / Z + b
当Z = n的时候,也就是最近的时候,Z’值最小,为0;
当Z = f的时候,也就是最远的时候,Z‘值最大,为1;
所以,得出如下的公式:
0 = a * 1 / n + b
1 = a * 1/ f + b
解这个一元一次方程组,得到如下的解:
a = fn / (n - f) , b = f / (f - n) (11)
所以,综合(7)(9)(11),我们得到:
X' = X / Z * (cot(a) / Aspect)
Y' = Y / Z * cot(a) (12)
Z ' =( fn/(n - f) ) * Z + f / (f - n)
W’ = 1
上面的变换最后用一个矩阵表示为:
[X, Y , Z , W] * M = [ X', Y', Z' , W']
得这个矩阵为:
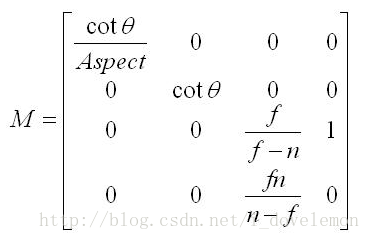
这个矩阵,和DirectX SDK中关于函数D3DXMatrixPerspectiveLH中使用的矩阵一致。它的来源就是这样的。
总结
矩阵变换是3D图形学不可缺少的一个工具,对于有志于深入学习的同学来说,不能过分依赖于API,而需要自己设计来完成这些功能。只有掌握所有这些细节,才能够建成更加高级的引擎。
参考资料:http://www.cnblogs.com/graphics/archive/2012/07/25/2582119.html
DirectX SDK 文档中Transform一节











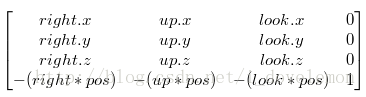














 1591
1591

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








