osgearth 设置物体的旋转

一、前言

        我们知道osg使用的是右手系。
其坐标轴定义为：
        X轴：向右（Right）、Y轴：向上（Up）、Z轴：向前（Forward）。
欧拉角的定义为：
        Heading（航向角）绕 Y轴 旋转。控制物体的 左右转向（如飞机绕垂直轴旋转）。
        Pitch（俯仰角）绕 X轴 旋转。控制物体的 上下俯仰（如飞机抬头或低头）。
        Roll（翻滚角）绕 Z轴 旋转。控制物体的 左右翻滚（如飞机绕机身纵轴旋转）。

而osgEarth 基于 OpenSceneGraph（OSG），但在地理空间中扩展了地理坐标系（如 WGS84）。其默认本地坐标系通常使用 ENU（东-北-天）坐标系。 
其坐标系定义为：
X轴：正东方向（East）、Y轴：正北方向（North）、Z轴：垂直向上（Up，天顶方向）。
虽然都是用了右手坐标系，但是坐标轴的朝向发生的变化。如下图所示：

x轴朝右，y指向正北，z轴垂直于地面，这里使用默认的ENU（东北天）坐标系。
osgearth的欧拉角定义为：
        Heading（航向角），绕 Z轴（垂直向上）旋转。
        Pitch（俯仰角），绕 X轴（东方向）旋转。
        Roll（翻滚角），绕 Y轴（北方向）旋转。

二、关键代码

有了以上的了解，设置一个物体的旋转直接使用内置的接口就好：

	//1）构建旋转矩阵
    osg::Matrix rotationMatrix;
	rotationMatrix.makeRotate(
    	osg::inDegrees(m_stRotation.dPitch), osg::Vec3d(1, 0, 0),
		osg::inDegrees(m_stRotation.dRoll), osg::Vec3d(0, 1, 0),
		osg::inDegrees(m_stRotation.dHeading), osg::Vec3d(0, 0, 1));
    //2）应用到节点
    osg::ref_ptr<osg::MatrixTransform> mt = new osg::MatrixTransform;
	mt->setMatrix(rotationMatrix);
    //3)添加到自己的节点
    mt->addChild(xxxx);//自己的节点 

注意顺序是以x轴、y轴、z轴的顺序，而不是heading、pitch、roll的顺序，这里不得不吐槽一下源码命名的随意性，说好的见名知意呢？让不熟悉的人使用这个接口，传值的顺序只能靠去猜了...

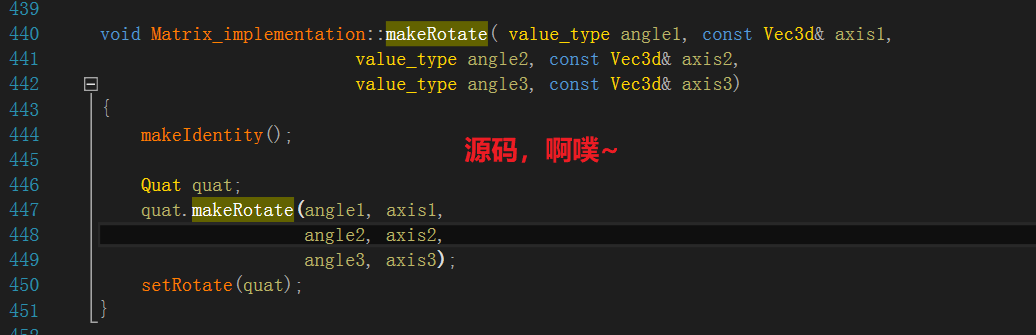
我直接上来就是heading、pitch、roll的顺序，错的找不到北(:0

三、效果

最后附上画局部坐标之后的代码

//创建坐标轴
osg::ref_ptr<osg::MatrixTransform> static CreateDebugAxis(double lngD, double latD, double height, double length = 1000000)
{
	osg::EllipsoidModel ellipsoid;
	// 计算ENU到世界坐标的变换矩阵
	osg::Matrixd localToWorld;
	ellipsoid.computeLocalToWorldTransformFromLatLongHeight(osg::inDegrees(latD), osg::inDegrees(lngD), height, localToWorld);

	// 创建变换节点并设置矩阵
	osg::ref_ptr<osg::MatrixTransform> mt = new osg::MatrixTransform;
	mt->setMatrix(localToWorld);

	mt->addChild(WHRadar::Util::GetDebugLine(osg::Vec3(0.0, 0.0, 0.0), osg::Vec3(length, 0.0, 0.0), osg::Vec4(255.0, 0.0, 0.0, 255.0)));
	mt->addChild(WHRadar::Util::GetDebugLine(osg::Vec3(0.0, 0.0, 0.0), osg::Vec3(0.0, length, 0.0), osg::Vec4(0.0, 255.0, 0.0, 255.0)));
	mt->addChild(WHRadar::Util::GetDebugLine(osg::Vec3(0.0, 0.0, 0.0), osg::Vec3(0.0, 0.0, length), osg::Vec4(0.0, 0.0, 255.0, 255.0)));
	return mt;
}

//获取调试线
osg::ref_ptr<osg::Geode>  static  GetDebugLine(osg::Vec3 point1, osg::Vec3 point2, osg::Vec4 color = osg::Vec4(255.0f, 0.0f, 0.0f, 1.0f))
{
	osg::ref_ptr<osg::Geode> geode = new osg::Geode();
	osg::ref_ptr<osg::Geometry> geometry = new osg::Geometry();
	osg::ref_ptr<osg::Vec3Array> points = new osg::Vec3Array();

	points->push_back(point1);
	points->push_back(point2);

	geometry->addPrimitiveSet(new osg::DrawArrays(osg::PrimitiveSet::LINES, 0, 2));
	geometry->setVertexArray(points);

	osg::ref_ptr<osg::Vec4Array> colors = new osg::Vec4Array;
	colors->push_back(color);
	colors->push_back(color);

	geometry->setColorArray(colors, osg::Array::BIND_PER_VERTEX);
	geometry->getOrCreateStateSet()->setAttribute(new osg::LineWidth(1.0), osg::StateAttribute::ON);

	geode->addDrawable(geometry.get());

	return geode;
}
//添加到场景
m_pRoot->addChild(WHRadar::Util::CreateDebugAxis(105, 35, 32000));

原创不易，记得点赞加关注哦，我会持续分享实用的功能（:-