斯坦福密码学课程-笔记-01-Introduction绪论

01-绪论 Introduction

Course Overview

Cryptography is everywhere

Secure communications:
web traffic: HTTPS
wireless traffic: 802.11i WPA2, GSM, Bluetooth
Encrypting files on disk: EFS, TrueCrypt
Content protection(e.g. DVD, Blu-ray): CSS, AACS
User authentication
… and much much more

Secure communication

Laptop $\leftrightarrow$ web server
protocol: HTTPS (actrual protocol: SSL/TLS)

Make sure that as this data travels across the network:

1. attacker can’t eavesdrop on this data
2. attacker can’t modify the data while it’s in the network

[no eavesdropping, no tampering]

Secure Sockets Layer/TLS

Two main parts:

1. Handshake Protocol: Establish shared secret key using public-key cryptography (2^nd part of course)
2. Record Layer: Transmit data using shared secret key
   Ensure confidentiality and integrity (1^st part of course)

Protected files on disk

1. attacker can’t read the contents in the file
2. if the attacker tries to modify the data in the file while it’s on disk, it will be detected when decrypting this file

Analogous to secure communication:
Alice today sends a message to Alice tomorrow.

Building block: symmetric encryption

E, D: cipher
k: secret key(e.g. 128bits)
m, c: plaintext, ciphertext

Encryption algorithm is publicly known
Never use a proprietary cipher

Use Cases

Single use key: (one time key)
Key is only used to encrypt one message
e.g. encrypted email: new key generated for every email

Multi use key: (many time key)
Key used to encrypt multiple messages
e.g. encrypted files: same key used to encrypt many files
Need more machinery than for one-time key

Things to remember

Cryptography is:

• A tremendous tool
• The basis for many security mechanisms

Cryptography is not:

• The solution to all security problems
• Reliable unless implemented and used properly
• Something you should try to invest yourself
  many many examples of broken ad-hoc designs

What is cryptography?

Crypto core

• Secret key establishment
• Secure communication

But crypto cand do much more

• Digital signatures
• Anonymous communication
• Anonymous digital cash
  Can I spend a “digital coin” without anyone knowing who I am?
  How to prevent double spending?

Protocols

• Examples:
  -Elections
  -Private auctions
• Secure multi-party computation

Goal: compute $f(x_1,x_2,x_3,x_4)$
trusted authority?
“Thm:” anything that can be done with a trusted authority, can also be done without a trusted authority.

Crypto magic

• Privately outsourcing computation
  
• Zero knowledge(proof of knowledge)
  

A rigorous science

The three steps in cryptography:

• Precisely specify threat model
• Propose a construction
• Prove that breaking construction under threat mode will solve an underlying hard problem

History

David Kahn, “The code breakers”(1996)

Symmetric Ciphers

Few Historic Examples (all badly broken)

1. Substitution cipher

e.g. Ceaser Cipher (no key)

Q: What is the size of key space in the substitution cipher assuming 26 letters?
A: $26!\approx 2^{88}$

How to break a substitution cipher?

Q: What is the most common letter in English text?
A: “E”

1. Use frequency of English letters
2. Use frequency of pairs of letters (diagrams)

2. Vigener cipher (16’th century, Rome)

3. Rotor Machines (1870-1943)

Early example: the Hebern machine (single rotor)

Most famous: the Enigma (3-5 rotors)
# rotor positions = $26^4\approx 2^{18}$
[total # keys = $2^{36}$ due to optional plugboard]

Data Encryption Standard (1974)

DES: # keys = $2^{56}$, block size = 64 bits

Today: AES(2001), Salsa20(2008),… (and others)

Discrete Probability

U: finite set (e.g. U = { 0 , 1 } n U=\{0, 1\}^n U={0,1}n)
Def: Probability distribution $P$ over $U$ is a function $P:U\to [0,1]$ such that $\sum _{x\in U}P(x)=1$

Examples:

1. Uniform distribution: for all $x\in U$: $P(x)=1/|U|$
2. Point distribution at $x_0$: $P(x_0)=1,\forall x\ne x_0:P(x)=0$

Distribution vector:
(Example) $(P(000),P(001),P(010),...,P(111))$

Event

• For a set $A\subseteq U:Pr[A]=\sum _{x\in A}P(x)\in [0,1]$
• The set $A$ is called an event
• note: $Pr[U]=1$

Example:
U = { 0 , 1 } 8 U=\{ 0, 1\}^8 U={0,1}8
A = { A=\{ A={all $x$ in $U$ that $ls{b}_2(x)=11\}\subseteq U$
for the uniform distribution on { 0 , 1 } 8 \{ 0, 1\}^8 {0,1}8：$Pr[A]=1/4$

[$ls{b}_2(x)=11$: the two least significant bits of the byte is “11”]

The union bond

For events $A_1$ and $A_2$
$$Pr[A_1\cup A_2]\le Pr[A_1]+Pr[A_2]$$

$A_1\cap A_2=\Phi ⟹Pr[A_1]\cup A_2=Pr[A_1]+Pr[A_2]$

Example:
A 1 = { A_1=\{ A1​={all $x$ in { 0 , 1 } n \{0,1\}^n {0,1}n s.t. $ls{b}_2(x)=11\}$
A 2 = { A_2=\{ A2​={all $x$ in { 0 , 1 } n \{0,1\}^n {0,1}n s.t. $ms{b}_2(x)=11\}$

$Pr[ls{b}_2(x)=11$ or $ms{b}_2(x)=11]=Pr[A_1\cup A_2]\le 1/4+1/4=1/2$

[$ls{b}_2(x)=11$: end with “11”]
[$ms{b}_2(x)=11$: begin with “11”]

Random Variables

Def: a random variable $X$ is a function $X:U\to V$

Example:
X : { 0 , 1 } n → { 0 , 1 } X: \{ 0, 1\}^n\rightarrow\{0, 1\} X:{0,1}n→{0,1}
X ( y ) = l s b ( y ) ∈ { 0 , 1 } X(y)=lsb(y)\in \{0, 1\} X(y)=lsb(y)∈{0,1}

For the uniform distribution on $U$:
$$Pr[X=0]=1/2,Pr[X=1]=1/2$$

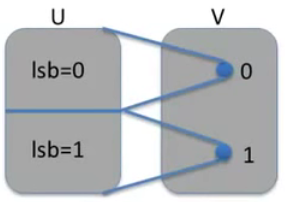
More generally:
rand.var. $X$ induces a distribution on $V$: $Pr[X=v]:=Pr[X^{-1}(v)]$

[$X^{-1}(v)$: $a$ for $X(a)=v$]
Formally we say that the probability that $X$ outputs $v$, is the same as the probability of the event that when we sample a random element in the universe, we fall into the pre-image of $v$ under the function $X$.

The uniform random variable

Let $U$ be some set, e.g. U = { 0 , 1 } n U=\{0, 1\}^n U={0,1}n
We write $r\stackrel{R}{\leftarrow }U$ to donate a uniform random variable over $U$
for all $a\in U$: $Pr[r=a]=1/|U|$
(formally, $r$ is the identity function: $r(x)=x$ for all $x\in U$)

Example:
Let $r$ be a uniform random variable on { 0 , 1 } 2 \{ 0, 1\}^2 {0,1}2
Define the random variable $X=r_1+r_2$
Then $Pr[X=2]=1/4$

(Hint: $Pr[X=2]=Pr[r=11]$)

Randomized algorithms

Deterministic algorithm: $y\leftarrow A(m)$

Randomized algorithm:
$y\leftarrow A(m;r)$ where r ← R { 0 , 1 } n r\xleftarrow{R}\{0, 1\}^n rR ​{0,1}n
output is a random variable
$y\stackrel{R}{\leftarrow }A(m)$

Example:
$A(m;k)=E(k,m)$, $y\stackrel{R}{\leftarrow }A(m)$

Independence

Def: events A and B independent if $Pr[A$ and $B]=Pr[A]\cdot Pr[B]$
random variables X, Y taking values in V are independent if $\forall a,b\in V:Pr[X=a$ and $Y=b]=Pr[X=a]\cdot Pr[Y=b]$

Example:
U = { 0 , 1 } 2 = { 00 , 01 , 10 , 11 } U=\{ 0, 1\}^2=\{00, 01, 10, 11\} U={0,1}2={00,01,10,11} and $r\stackrel{R}{\leftarrow }U$
Define random variables $X$ and $Y$ as: $X=lsb(r)$, $Y=msb(r)$
$Pr[X=0$ and $Y=0]=Pr[r=00]=1/4=Pr[X=0]\cdot Pr[Y=0]$

XOR

XOR of two strings in { 0 , 1 } n \{ 0, 1\}^n {0,1}n is their bit-wise addition mod 2

An important property of XOR

$Y$ is a random variable over { 0 , 1 } n \{ 0, 1\}^n {0,1}n
$X$ is a uniform random variable over { 0 , 1 } n \{ 0, 1\}^n {0,1}n
$X$ and $Y$ are independent
Then: $Z:=Y\oplus X$ is a uniform variable on { 0 , 1 } n \{ 0, 1\}^n {0,1}n

Proof: (for n=1)
$Pr[Z=0]=Pr[(X,Y)=(0,0)$ or $(X,Y)=(1,1)]=Pr[(X,Y)=(0,0)]\cdot Pr[(X,Y)=(1,1)]=1/2$

The birthday paradox

Let $r_1,r_2,...,r_n\in U$ be independent identically distributed random variables.
when $n=1.2\times |U{|}^{1/2}$ then $Pr[\exists i\ne j:r_i=r_j]\ge 1/2$
[notation: $|U|$ is the size of $U$]

Example:
Let U = { 0 , 1 } 128 U=\{ 0, 1\}^{128} U={0,1}128
After sampling about $2^{64}$ random messages from $U$, some two sampled messages will likely be the same.