直流电机磁场
下面是直流电机(可以看看自己的电动小马达内部)的磁场分布
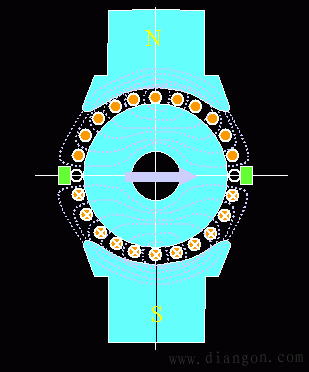
我们可以看到,直流电机的磁场有励磁磁场和电枢磁场。其中上下两块磁体产生励磁磁场,方向从N->S。还有一个与励磁磁场垂直的电枢磁场。图中表明了方向(可以用右手定则来判断磁场方向,x是电流流入的方向,o是电流流出的方向,最后可以判断出磁场方向从左向右)。如果两片电枢的的轴线不是和励磁磁场垂直,那么励磁磁场和电枢磁场也会有一个夹角,通常电枢磁场总是和电刷的轴线重合。
我们把主极(电磁磁场d)的轴线称为直轴,与直轴垂直的的轴线(电枢磁场q)称为交轴。
说了这么多了总算是把dq引出来了。然而这只是一个类比而已,其实dq坐标系是没有物理意义的,是人们假想的坐标系。
感应电机磁场
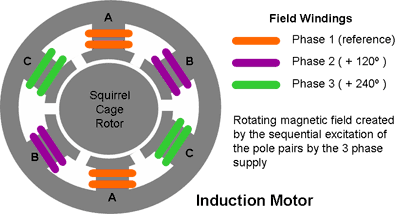
上面是三相感应电机的原理示意图。定子上有绑线圈的,并且可以接上交流电。如果这三个接上了相位相差120的同等正弦交流电会产生什么效果呢?每一个交流都会在线圈上产生磁场,然后三个磁场叠加,
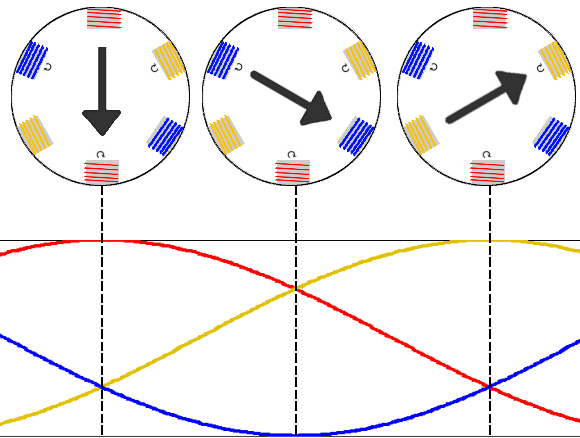
最后就会变成如图所示的旋转磁场。而转子是闭合的线圈,定子产生的旋转磁场切割转子的闭合线圈,将会产生感应电流,感应电流在磁场会产生安培力,安培力驱动转子转动。最后产生的效果如下

三相感应电机的数学方程式非常复杂的,而且电机的很多控制参数在方程式耦合在一起的,如果想要单独控制是不可能的,那么该怎么办呢?有人发现了dq坐标系可以解决这个问题。
简单说可以用下面的图表示(其实一般我们都是把dq坐标系放在转子的旋转磁场上)
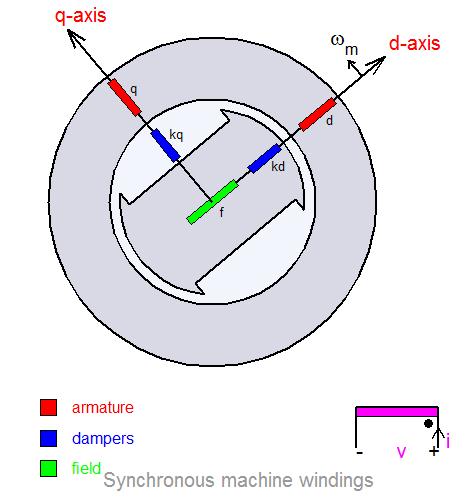
具体如下图
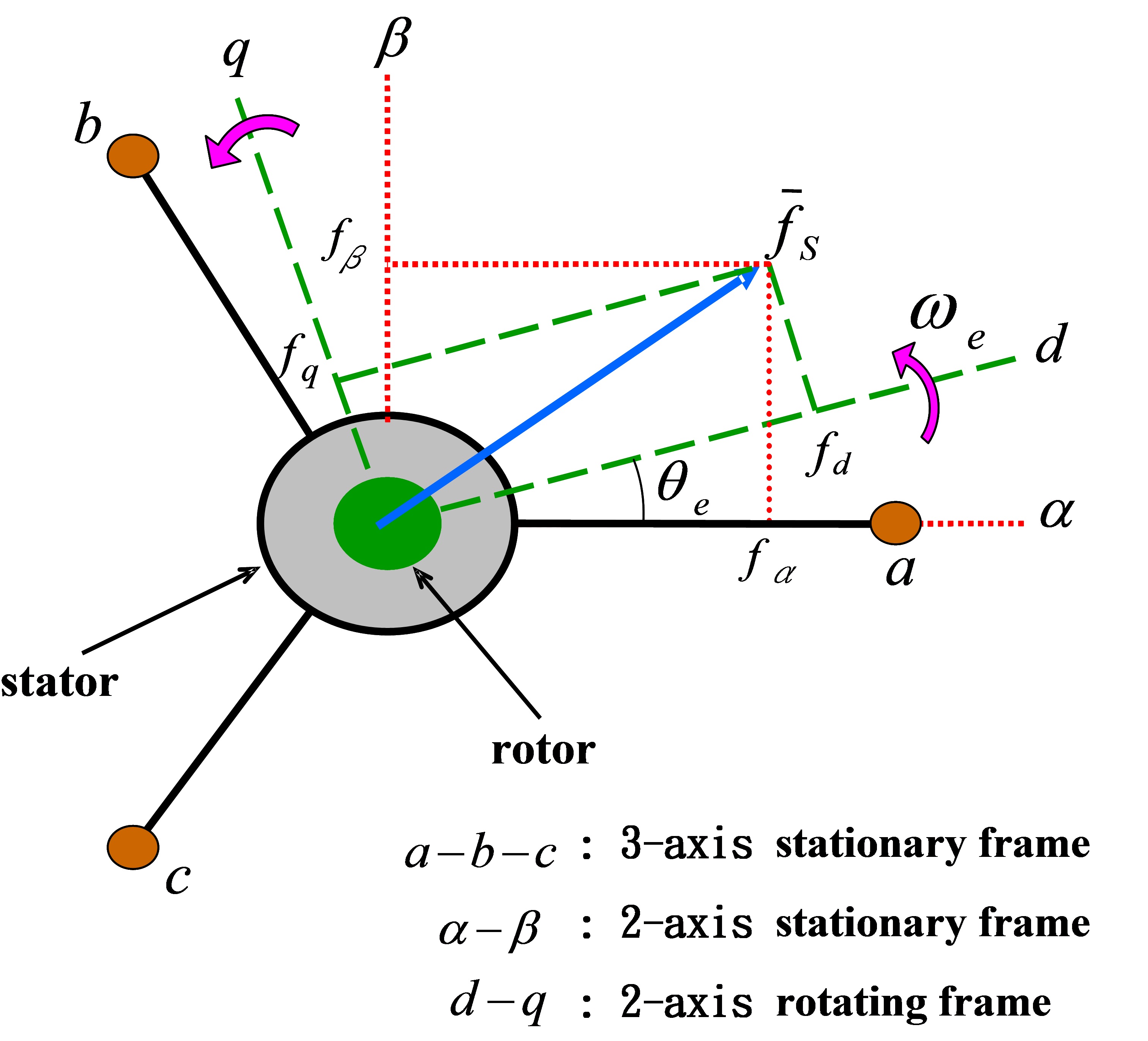
上面的图初看很复杂,没关系,分解开来看。
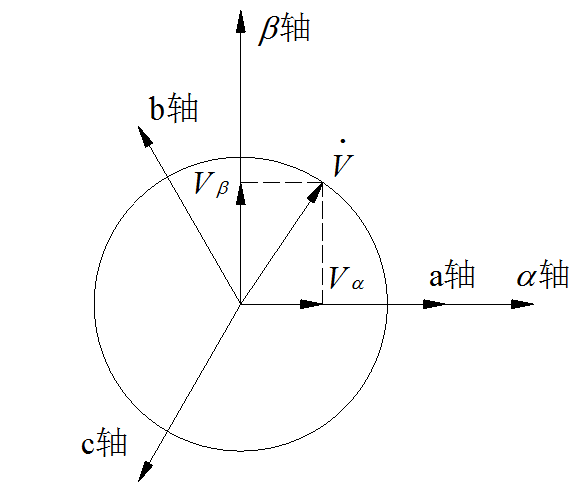
abc会产生一个旋转磁场V(矢量),这个矢量的大小不变,旋转的角速度不变。如果这个矢量投影到alpha和beta上,则有
Vα=V∗cosα
Vβ=V∗sinα
这个就是克拉克变换,三相静止到两厢静止(3s/2s)。
具体就是下面
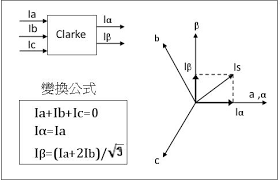
那么如果我们的静止坐标系
αβ
以某个角速度旋转起来,比如这个角速度的值和定子产生的旋转磁场的角速度相同。那么是不是旋转磁场与
αβ
坐标系是不是相对静止了呢?此时这个旋转的
αβ
坐标系我们就称为dq坐标系吧(这才是真正的dq坐标系)。dq坐标系与
αβ
坐标系之间的关系如下
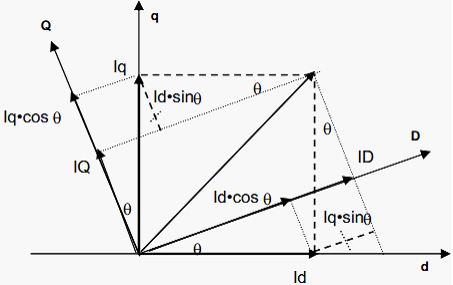
与之对应的就是park变换,两相静止到两相旋转(2s/2r)
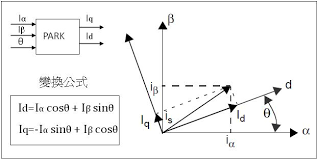
不过park变化我们一般说的都是三相静止到亮相旋转(3s/2r)
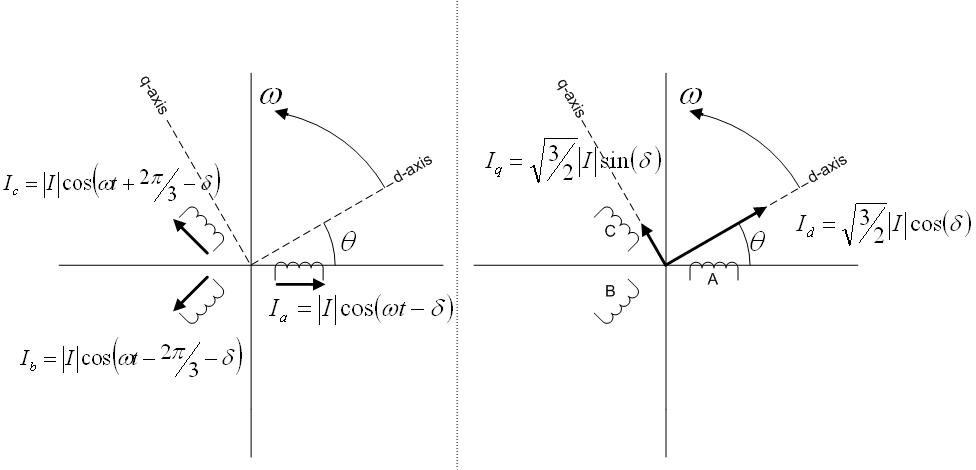
转子磁动势
设转子转速为n,转差率为s,定子产生的旋转磁场的同步转速为
ns
,则气隙磁场B将以
Δn=ns−n=sns
的相对速度切割转子绕组。
Δn
称为转差。此时转子绕组的感应电动势E和转子产生的电流I的频率
f2
应为
f2=pΔn60=pns60s=sf1
.
f2
称为转差频率。频率为
f2
的转子电流将产生转子旋转磁动势F。F相对于转子的转速
n2=60f2p=60sf1p=sns=Δn
.
由于转子本身以转速n在旋转,因此从定子侧观察时,F在空间的转速应该为
n2+n=Δ+n=ns
这说明无论转子的实际转速是多少,转子磁动势F在空间的转速总是等于定子磁动势转速,并且和定子磁动势保存相对静止。
转载于http://blog.csdn.net/he_wen_jie/article/details/51106676








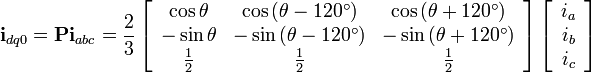
















 3万+
3万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








