Maximum entropy modeling (一)
0.
初次接触最大熵的时候,有点觉得无厘头,因为熵是代表信息的混乱程度,那么最大熵不就是最大化信息的混乱程度?这样的模型能用吗?后来看了基本概念,最大熵是有前提的,就是要在保持我们的模型在符合已知信息的情况下,对未知信息保持最大熵。这个定义就简单明了的说明了最大熵的意义和条件。但具体如何应用呢?很多事情我们都是有个概念,但是对于具体怎么实现呢?在数学上的表现形式是什么呢?接下来根据自己的理解和部分参考文献介绍最一下大熵这个问题,争取做到既简单又明了。主要参考《a maximum entropy approach to natural language processing》。
1.
要对一个随机过程或者事件进行建模,要完成两个任务:1.决定有哪些捕捉到了这个随机过程或事件的统计量;将这些得到的统计量或者说facts用模型关联起来。
2.
这里首先从一个实际的例子出发来引入maximum entropy的概念。
假定我们现在面临的任务是:把英语单词in翻译成法语。我们的模型用p(f)来表示把这个单词翻译成法语单词f的概率。为了能够更加准确的把in这个单词正确的翻译出来,我们收集了许多以前的翻译样本,这些我们收集的以前的翻译样本就构成了我们的训练集。现在我们应当做什么呢?自然是要先从收集的训练集中提取尽可能多和准确的有用的信息,然后把这个信息用来帮助我们构建我们的模型,其实就是用这个信息来合理的约束我们的模型,最后就用构建的模型来实现我们起初的任务。
现在就要从训练集中提取信息了。通过观察,我们发现在训练集中in这个单词经常会被翻译为以下5个单词中一个:{dans, en, à, au cours de, pendant }.利用这个信息,我们可以对我们的模型施加第一个约束,(一个泛泛的模型太多了,通过训练集中的信息逐步的施加约束,逐步的缩小模型的可行范围,到最后就可以确定求解出具体的模型了)。这个约束可以写成:

上面的这个模型就是对这5个词均匀分配,谁也不偏重,因为没有信息告诉我们要偏重谁啊,所以这个做法最保险,因为没有违背我们已知的信息(会被翻译成这5个词),也没有施加别的我们未知的假设。
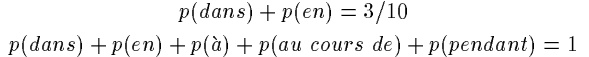
3.
有了上面比较直观的例子后,接下来以比较正式的方式介绍最大熵建模。
对于建模来说,我们的任务可以认为是要考虑一个输出为![]() 的随机过程,然后构建一个可以准确表示这个过程的模型。具体到上面翻译的那个例子中,这个过程就是要产生一个in的对应翻译输出
的随机过程,然后构建一个可以准确表示这个过程的模型。具体到上面翻译的那个例子中,这个过程就是要产生一个in的对应翻译输出![]()
![]() . 而产生y的这个过程可能会利用到别的context信息(例如上边我们发现的in后面跟着什么词有可能会被翻译成什么等)假定为
. 而产生y的这个过程可能会利用到别的context信息(例如上边我们发现的in后面跟着什么词有可能会被翻译成什么等)假定为![]() .
. ![]() .(其中
.(其中![]() 就是所有的对应元素y,x,p组成的集合)
就是所有的对应元素y,x,p组成的集合)
给了一堆训练数据,要构建一个模型,直接面临的两个问题就是0. 如何找到在训练集中有用的信息?1.怎么来表达训练集中的这些信息?2.怎么样让我们的模型来体现这个找到的信息,下面3.1,3.2就是解决1.2.这两个问题的。也就是假设我们已经知道了哪些是有用的信息。关于如何找到这些信息,可以参考接下来的第4部分。(这里是按照文章结构顺序来写的,还请大家多多包涵哈)。
3.1
我们把训练数据用(x_1,y_1), (x_2,y_2),…, (x_n,y_n)来表示。具体到翻译的例子中,x就是在in周边的单词,y就是过程的输出量。得到这些训练数据后,要通过一种数学的形式把它们表现出来,对于生成式模型而言,莫过于就是用概率来表示。于是我们用训练数据的经验分布来表示他们,也就是频率构建的分布:
3.2
有了上面的对训练数据的表示,我们的模型的任务自然就是要能够产生generate这些训练数据![]() ,并把已知的信息利用上去,比如in被翻译成dans和en的频率是30%,被翻译成dans和au cours de的频率是50%等。这些信息是独立于in的应用环境的,是一个总体上的统计,我们还可以发现一些与应用环境上下文有关的信息,比如in后面跟着April时,它有90%的时候会被翻译成en。
,并把已知的信息利用上去,比如in被翻译成dans和en的频率是30%,被翻译成dans和au cours de的频率是50%等。这些信息是独立于in的应用环境的,是一个总体上的统计,我们还可以发现一些与应用环境上下文有关的信息,比如in后面跟着April时,它有90%的时候会被翻译成en。
F相对于经验分布的期望值就可以认为是在大量样本中平均来说应当观察到f的次数,可以用这个期望来表示在训练样本中的f的信息,即:
类似于上面的表示方法,我们可以把其他的观察量也表示为指示函数的期望的形式。
当我们构建模型是,毫无疑问,最好是f通过模型所体现的信息和f在训练样本中体现的信息相同,于是可以得到我们要求f相对于模型的期望应当等于f相对于经验分布的期望。而f相对于模型的期望可以表达为:
联立(1)(2)(3)就可以得到对模型的一个约束,即为:
3.3
假如我们按照3.1,3.2的方式得到了n个特征函数f_i,对应的也会有n个对模型p的约束条件:
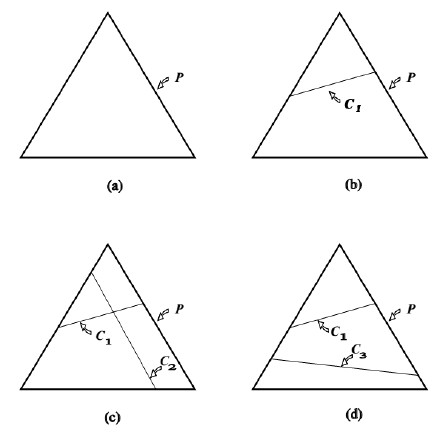
C的作用就如下图所示:
上述部分相当于给出了所设计的模型应当满足哪些条件,从训练数据中提取出了一些信息来对模型进行约束,接下来要解决的是在满足约束条件的所有模型中又应当如何具体选择呢?最大熵原理是要选择哪些最均匀分配最uniform的分布。但是什么是uniform的distribution呢?(这里不是特指均匀分布,请注意哈)。对于一个分布的均匀性的一个数学衡量标准是熵,而对于一个条件分布(我们的模型是要求p(y|x)哦),衡量它的均匀性的标注就是条件熵,表示为:
其推导过程为:
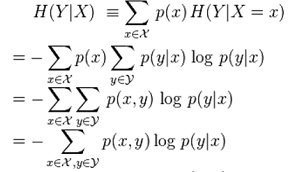
由上面条件熵的表达式(5)可以很容易的推出:0≤H≤log|Y|,当条件分布p(y|x)是均匀分布时,H取最大值,可以代入验证。
有了条件熵的定义,就可以得到最大熵原理:
![]() :
: ![]()
最大熵的一个优点是通常情况下,上面的最优化问题都是有唯一解的。但是不排除个别个别的例外。
3.4
得到了最优化表达式,接下来就是求解了,可以用拉格朗日乘子法求解。
0.
1.
2. ![]() 时,Λ达到最大值,用
时,Λ达到最大值,用![]() 表示这个最大值,即有
表示这个最大值,即有
具体表达式可以求出为:
4. ![]() 是对偶问题的解,那么
是对偶问题的解,那么![]() 就是原问题的解。这样就可以先求解4,即最大化
就是原问题的解。这样就可以先求解4,即最大化![]() 求出最优解
求出最优解![]() ,然后结合3中的表达式求解原问题1的最优解
,然后结合3中的表达式求解原问题1的最优解![]() 。
。
3.5
上一个部分3.4讲解了求出问题4的最优解lambda,就可以求出原问题的最优解p。那么如何求lambda呢?这一部分就解决这个问题。
因为问题4就是一个无约束优化问题,可以用最表上升,梯度上升等方法求解。这里就不细讲了,嘻嘻。
4.
至此其实最大熵已经介绍完了,就是上面的第三部分。只是了解一下最大熵的,下面的不看也行。但是为了应用的完整性,我们还是忠实于原文加入接下来的内容。但也正因为不是主要部分,所以接下来也不会特别详细介绍。
上面第三部分解决了加入我们知道了要利用的训练样本中的信息,那么如何去表达和如何让模型去体现这个信息,以及怎样求解这个模型。接下来,这一部分解决的问题是最开始的一步,即如何找到那些训练集中所谓‘有用’的信息呢?(这里只是这篇文章针对于上面的那个例子的做法,如果我们自己应用是可以用别的方法来得到我们需要的features的。)
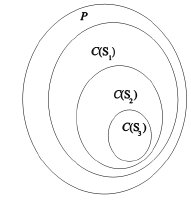
![]() ,也就是要所选择的特征在目前的模型上的期望要与数据期望相等,在与S对应的模型C(S)中肯定只有一部分满足条件,我们记为C(S∪f),用图来表达如下:
,也就是要所选择的特征在目前的模型上的期望要与数据期望相等,在与S对应的模型C(S)中肯定只有一部分满足条件,我们记为C(S∪f),用图来表达如下:
(这一部分讲的比较大略,因为与本文的主题最大熵并没有直接的关系,只是对应于本文的一个具体例子的一部分。详情可看参考文献原文哈)
5.
参考文献:《a maximum entropy approach to natural language processing》。








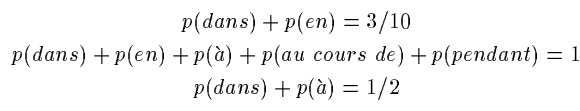
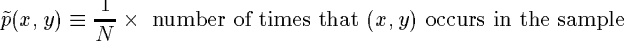
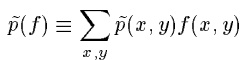

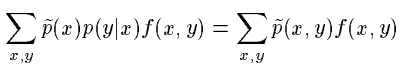

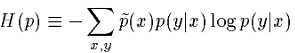
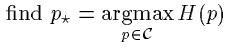
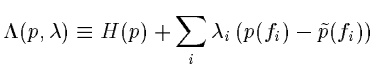
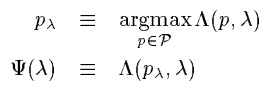
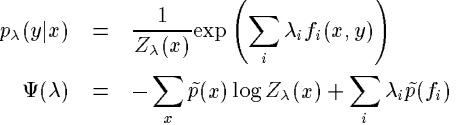
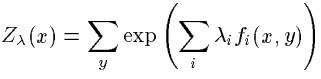
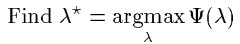
















 153
153

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








