(3-3)蒙特卡洛方法：算法的探索与策略改进

在蒙特卡洛控制中，探索和策略改进是紧密相关的。智能体需要在探索中积累经验，然后使用这些经验来改进策略。其中ε-贪婪策略是一种常见的平衡探索和利用的方法，通过在一定程度上随机选择动作，保证了探索的进行，同时又利用了当前的最佳估计。总之，蒙特卡洛控制通过探索和策略改进来学习最优策略，探索帮助智能体了解环境，策略改进通过估计值函数来选择最佳动作。这两个方面是强化学习中非常重要的概念，它们共同促进了智能体在不断学习和提高性能。

3.3.1  探索与利用的平衡再探讨

探索与利用的平衡是强化学习中一个非常关键的概念。在蒙特卡洛控制和其他强化学习算法中，智能体需要在探索和利用之间取得平衡，以便有效地学习和改进策略。

1. 探索的重要性

1. 探索是指智能体尝试不同的动作或策略，以了解环境的特性。在强化学习中，初始时智能体通常对环境一无所知，因此需要通过探索来积累经验。
2. 如果智能体始终选择当前认为最佳的动作，那么它可能会陷入固定的策略中，无法发现更好的策略。因此，探索是学习的前提条件。

2. 利用的重要性

1. 利用是指智能体根据其已有的知识或经验来选择动作，以最大化累积奖励。一旦智能体学到了一些有关环境的信息，它应该利用这些信息来获得更多的奖励。
2. 如果智能体过于强调探索，那么它可能会浪费时间在不必要的随机动作上，而错过了已知好策略的机会。因此，利用是获得高性能策略的关键。

3. ε-贪婪策略

1. ε-贪婪策略是一种常见的方法，用于平衡探索和利用。根据ε的设定，智能体以一定的概率ε随机选择动作，以便在状态空间中进行探索；以1-ε的概率选择当前认为最佳的动作，以最大化奖励。
2. 通过调整ε的值，可以控制探索与利用的权衡。较大的ε值会促使更多的探索，而较小的ε值会促使更多的利用。

4. 随时间递减的ε

一种常见的做法是随着时间的推移逐渐减小ε的值。在开始时，可以使用较大的ε来鼓励更多的探索，然后随着智能体积累更多经验，逐渐降低ε，以便更多地利用已知的信息。

5. 探索函数

探索函数是一种方法，可以根据状态或状态-动作对的访问次数来估计哪些部分的状态空间需要更多的探索。这有助于智能体将有限的资源用于最需要的地方。

请看下面的例子，演示了使用ε-贪婪策略平衡探索与利用，以解决一个多臂老虎机问题（Multi-Armed Bandit Problem）。在这个问题中，智能体需要在多个老虎机（每个老虎机对应一个动作）之间进行选择，以最大化累积奖励。

实例3-5：解决多臂老虎机问题（源码路径：daima\3\tiger.py）

实例文件tiger.py的具体实现代码如下所示。

import numpy as np
import matplotlib.pyplot as plt

# 定义多臂老虎机问题
num_actions = 10  # 有10个动作（10个老虎机）
true_action_values = np.random.randn(num_actions)  # 随机生成每个老虎机的真实价值
num_steps = 1000  # 总步数
epsilon = 0.1  # ε-贪婪策略中的ε

# 初始化动作值估计和动作选择次数
action_values = np.zeros(num_actions)
action_counts = np.zeros(num_actions)

# 记录每步的累积奖励
total_rewards = []

# 强化学习主循环
for step in range(num_steps):
    if np.random.rand() < epsilon:
        # 以概率ε随机选择动作（探索）
        action = np.random.choice(num_actions)
    else:
        # 以概率1-ε选择当前估计最高的动作（利用）
        action = np.argmax(action_values)

    # 模拟选择动作后获得的奖励
    reward = np.random.normal(true_action_values[action], 1.0)

    # 更新动作值估计和动作选择次数
    action_counts[action] += 1
    action_values[action] += (reward - action_values[action])

    # 记录累积奖励
    total_rewards.append(reward)

# 绘制累积奖励曲线
plt.plot(np.cumsum(total_rewards) / np.arange(1, num_steps + 1))
plt.xlabel("步数")
plt.ylabel("累积奖励")
plt.title("ε-贪婪策略的探索与利用平衡")
plt.show()

在上述代码中，使用了ε-贪婪策略来平衡探索与利用。智能体在每一步中以概率ε随机选择动作（探索），以概率1-ε选择当前估计最高的动作（利用）。通过这种平衡，智能体可以不断学习哪些老虎机更有可能产生高奖励。上述代码中的奖励是通过随机模拟生成的，而每个老虎机的真实价值是随机生成的，因此智能体必须通过不断尝试不同的动作来逐渐学习哪个动作具有最高的价值。最后，绘制了累积奖励随时间的变化，展示了智能体如何在探索与利用之间取得平衡，并逐渐提高累积奖励。执行效果如图3-8所示。这是一个折线图，其中横轴表示时间步数（从1到num_steps），纵轴表示累积奖励的平均值。随着时间的推移，您可以观察到累积奖励是否逐渐上升，这表明智能体逐渐学会了选择更好的动作，以最大化奖励。

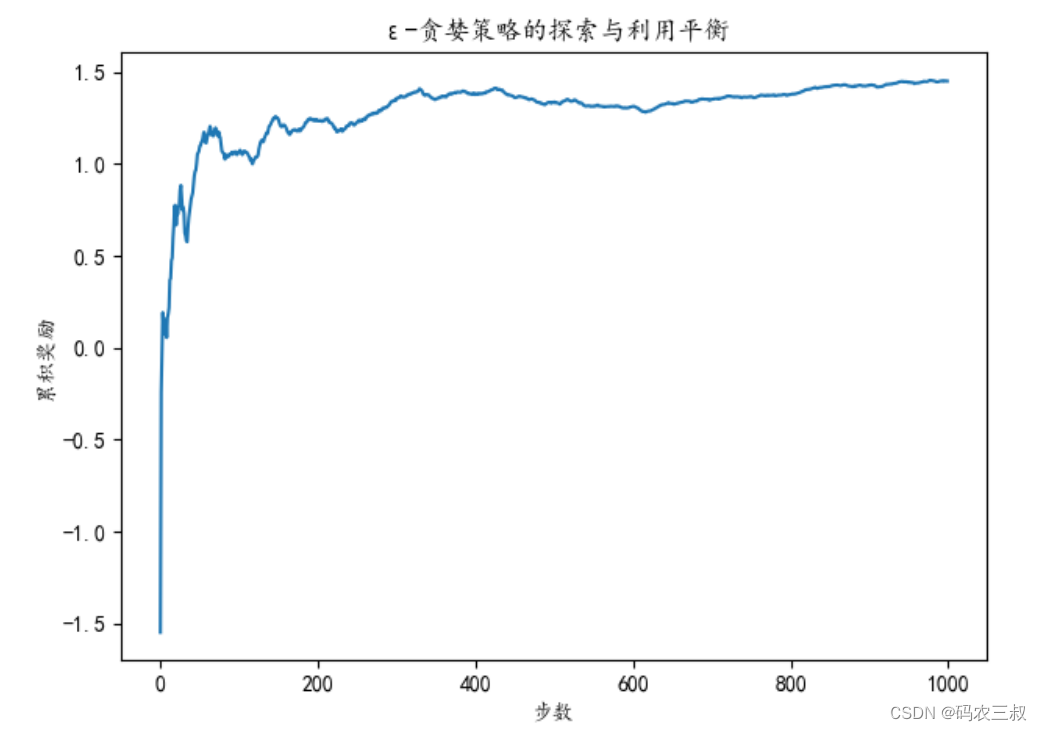
图3-8  累积奖励随着时间步数的变化图

总之，探索与利用的平衡是强化学习中的一个核心挑战。合理的探索策略可以帮助智能体积累经验，发现潜在的高性能策略；而合理的利用策略可以确保智能体充分利用已知的信息来最大化奖励。ε-贪婪策略和递减的ε值是常用的方法来实现这一平衡。在实际应用中，需要根据具体问题和算法进行调整和优化。

3.3.2  贪婪策略与ε-贪婪策略的比较

贪婪策略（Greedy Policy）和ε-贪婪策略（ε-Greedy Policy）是两种不同的策略选择方法，用于平衡探索与利用。

1. 贪婪策略（Greedy Policy）

1. 特点：在贪婪策略中，智能体总是选择当前认为最佳的动作，以最大化累积奖励。这意味着智能体完全依赖于已有的知识或经验，不进行随机探索。
2. 应用：贪婪策略在已经具有高度可信动作值估计的情况下，可以用于最大化累积奖励。它适用于问题已经非常清楚和稳定的情况。

2. ε-贪婪策略（ε-Greedy Policy）

1. 特点：ε-贪婪策略引入了一定程度的随机性。在每一步中，智能体以概率ε随机选择动作（探索），以概率1-ε选择当前认为最佳的动作（利用）。
2. 应用：ε-贪婪策略用于平衡探索与利用。在问题初始阶段或需要继续探索的情况下，这种策略非常有用。通过调整ε的值，可以控制探索的程度。较小的ε值更注重利用已知信息，而较大的ε值更注重探索未知动作。

3. 比较

贪婪策略更适用于已知问题或稳定的环境，其中动作值估计非常可靠。它可以最大化累积奖励，但可能错过了探索新动作的机会。

1. ε-贪婪策略提供了一种平衡探索和利用的方法。它适用于初期不了解环境的情况，以及需要保持一定程度的探索以发现更好策略的情况。
2. ε的选择是关键，较大的ε值更强调探索，较小的ε值更强调利用。合理的ε选择取决于问题的性质和目标。

总之，贪婪策略和ε-贪婪策略都有其用武之地，具体选择取决于问题的性质和学习的阶段。探索与利用的平衡是强化学习中的一个重要挑战，需要根据具体情况来进行调整和优化。

请看下面的例子，功能是比较贪婪策略和ε-贪婪策略，并通过数据进行对比。在这个示例中，我们将考虑一个简化的多臂老虎机问题，其中有多个老虎机（动作），每个老虎机的奖励是从不同的正态分布中随机生成的。

实例3-6：在老虎机中比较贪婪策略和ε-贪婪策略（源码路径：daima\3\bi.py）

实例文件bi.py的具体实现代码如下所示。

plt.rcParams["axes.unicode_minus"]=False #解决图像中的"-"负号的乱码问题
plt.rcParams['font.sans-serif']=['kaiti']
# 定义多臂老虎机问题
num_actions = 10  # 10个老虎机
true_action_values = np.random.randn(num_actions)  # 随机生成每个老虎机的真实价值
num_steps = 1000  # 总步数

# 初始化动作值估计和动作选择次数
action_values_greedy = np.zeros(num_actions)  # 贪婪策略的动作值估计
action_values_epsilon = np.zeros(num_actions)  # ε-贪婪策略的动作值估计
action_counts_greedy = np.zeros(num_actions)  # 贪婪策略的动作选择次数
action_counts_epsilon = np.zeros(num_actions)  # ε-贪婪策略的动作选择次数

# 记录每步的累积奖励
total_rewards_greedy = []
total_rewards_epsilon = []

epsilon = 0.1  # ε-贪婪策略中的ε

# 强化学习主循环
for step in range(num_steps):
    # 贪婪策略：选择当前估计最高的动作
    action_greedy = np.argmax(action_values_greedy)
    # ε-贪婪策略：以概率ε随机选择动作，以概率1-ε选择当前估计最高的动作
    if np.random.rand() < epsilon:
        action_epsilon = np.random.choice(num_actions)
    else:
        action_epsilon = np.argmax(action_values_epsilon)

    # 模拟选择动作后获得的奖励
    reward = np.random.normal(true_action_values[action_greedy], 1.0)

    # 更新动作值估计和动作选择次数
    action_counts_greedy[action_greedy] += 1
    action_counts_epsilon[action_epsilon] += 1
    action_values_greedy[action_greedy] += (reward - action_values_greedy[action_greedy])
    action_values_epsilon[action_epsilon] += (reward - action_values_epsilon[action_epsilon])

    # 记录累积奖励
    total_rewards_greedy.append(reward)
    total_rewards_epsilon.append(reward)

# 打印贪婪策略的步数和奖励
print("贪婪策略：")
print("总步数:", num_steps)
print("总奖励:", sum(total_rewards_greedy))

# 打印ε-贪婪策略的步数和奖励
print("ε-贪婪策略：")
print("总步数:", num_steps)
print("总奖励:", sum(total_rewards_epsilon))

# 绘制累积奖励曲线
plt.figure(figsize=(10, 5))

plt.subplot(1, 2, 1)
plt.plot(np.cumsum(total_rewards_greedy) / np.arange(1, num_steps + 1), label="贪婪策略")
plt.xlabel("步数")
plt.ylabel("累积奖励")
plt.title("贪婪策略的累积奖励")

plt.subplot(1, 2, 2)
plt.plot(np.cumsum(total_rewards_epsilon) / np.arange(1, num_steps + 1), label="ε-贪婪策略")
plt.xlabel("步数")
plt.ylabel("累积奖励")
plt.title("ε-贪婪策略的累积奖励")

plt.tight_layout()
plt.show()

对上述代码的具体说明如下：

1. 设置图形参数，以解决图像中的负号乱码问题，并指定中文字体。
2. 定义了一个多臂老虎机问题，其中有10个老虎机，并为每个老虎机生成了随机的真实价值。
3. 初始化了两种策略的动作值估计、动作选择次数和累积奖励记录。
4. 在一个主循环中，使用贪婪策略和ε-贪婪策略选择动作，模拟选择动作后获得的奖励，并根据奖励更新动作值估计和动作选择次数。
5. 打印了贪婪策略和ε-贪婪策略的总步数和总奖励。
6. 绘制了两种策略的累积奖励曲线，用于比较它们的性能。

注意：在上述代码中，两种策略都从相同的初始状态开始，动作值估计都初始化为零。这意味着在初始阶段，它们会探索相同的动作，所以会收到相似的奖励反馈。另外，模拟选择动作后获得的奖励是从正态分布中随机生成的，因此奖励分布相对稳定，所以也会这导致两种策略在选择动作后的奖励反馈上没有明显的差异。

3.3.3  改进探索策略的方法

在实际应用中，改进探索策略的方法有很多，其中常见的方法如下所示：

1. ε-贪婪策略中的ε参数调整：ε-贪婪策略通过控制ε参数来平衡探索和利用。可以尝试不同的ε值，根据问题的性质选择合适的探索率。较大的ε值会增加探索的机会，而较小的ε值会更倾向于利用已知的最优策略。
2. Softmax策略：Softmax策略通过使用Softmax函数来计算每个动作的概率分布，使得非最佳动作仍然有一定概率被选择。Softmax策略的温度参数可以调整探索的程度，较高的温度将增加探索，而较低的温度将减少探索。
3. UCB（Upper Confidence Bound）算法：UCB算法基于不确定性来选择动作。它使用动作的置信上限来进行决策，从而鼓励探索未知的动作，但在不确定性较低时选择已知的最佳动作。
4. 随机策略：在一些情况下，完全随机选择动作可能是一种探索策略，尤其是在初始阶段，以便探索环境并收集奖励信息。
5. 自适应探索策略：有一些自适应探索策略，如Thompson采样或Bayesian优化，可以根据之前的经验自动调整探索策略，以提高性能。
6. 经验回放（Experience Replay）：在强化学习中，经验回放可以帮助探索更广泛的状态空间。它存储之前的经验并随机从中提取样本进行训练，以改善策略。
7. 多臂老虎机问题的上限估计：在多臂老虎机问题中，可以使用上限估计方法，如UCB1算法，来提高探索效率。
8. 探索激励：引入探索激励，例如奖励函数中的随机性或时间相关性，可以鼓励智能体在不同的状态下进行探索。

选择适当的探索策略取决于具体问题的性质和需求，通常需要在不同策略之间进行实验和调整，以找到最适合问题的探索方法。请看下面的例子，演示了使用 Upper Confidence Bound (UCB) 算法改进探索策略的例子。

实例3-7：在老虎机中比较贪婪策略和ε-贪婪策略（源码路径：daima\3\gai.py）

Upper Confidence Bound (UCB) 算法是一种用于解决多臂老虎机问题（Multi-Armed Bandit Problem）的强化学习算法。多臂老虎机问题是一个经典的探索与利用问题，其中一个代理需要在有限的时间内决定选择哪个动作以最大化累积奖励。UCB 算法的核心思想是在探索和利用之间取得平衡，通过对每个动作的不确定性估计来决定动作的选择。UCB 算法的一般步骤如下：

（1）初始化每个动作的估计值（通常为零）和选择次数（初始化为零）。

（2）在每个时间步骤 t，计算每个动作的上置信界（Upper Confidence Bound），用于估计该动作的真实价值可能的上限。

（3）选择具有最高上置信界的动作，即 argmax(Upper Confidence Bound)。

（4）执行所选择的动作并观察获得的奖励。

（5）更新所选择动作的估计值和选择次数。

（6）重复步骤 2 到步骤 5，直到达到预定的时间步数或回合数。

实例文件gai.py的具体实现代码如下所示。

import numpy as np
import matplotlib.pyplot as plt

# 定义多臂老虎机问题
num_actions = 10  # 10个老虎机
true_action_values = np.random.randn(num_actions)  # 随机生成每个老虎机的真实价值
num_steps = 1000  # 总步数

# 初始化动作值估计和动作选择次数
action_values = np.zeros(num_actions)  # 动作值估计
action_counts = np.zeros(num_actions)  # 动作选择次数
total_rewards = []  # 记录每步的累积奖励

# UCB参数
c = 2.0  # 探索参数，可以根据需要调整

# 强化学习主循环
for step in range(num_steps):
    # UCB算法选择动作
    ucb_values = action_values + c * np.sqrt(np.log(step + 1) / (action_counts + 1e-5))
    action = np.argmax(ucb_values)

    # 模拟选择动作后获得的奖励
    reward = np.random.normal(true_action_values[action], 1.0)

    # 更新动作值估计和动作选择次数
    action_counts[action] += 1
    action_values[action] += (reward - action_values[action])

    # 记录累积奖励
    total_rewards.append(reward)

# 打印总步数和总奖励
print("总步数:", num_steps)
print("总奖励:", sum(total_rewards))

# 绘制累积奖励曲线
plt.plot(np.cumsum(total_rewards) / np.arange(1, num_steps + 1), label="UCB")
plt.xlabel("步数")
plt.ylabel("累积奖励")
plt.title("UCB算法的累积奖励")
plt.legend()
plt.show()

在上述代码中，我们使用 UCB 算法来选择动作，以便更加关注尚未探索或估计值不确定的动作。UCB 算法的探索参数 c 可以根据需要进行调整，以平衡探索和利用。通过使用 UCB 算法，智能体可以在不断学习的同时，更多地选择具有潜在高价值的动作，从而提高了性能。执行后输出下面的结果，并绘制了累积奖励曲线图，如图3-8所示。这张图显示了智能体在每个时间步骤中累积的奖励随时间的变化。

总步数: 1000
总奖励: 1358.9627909351584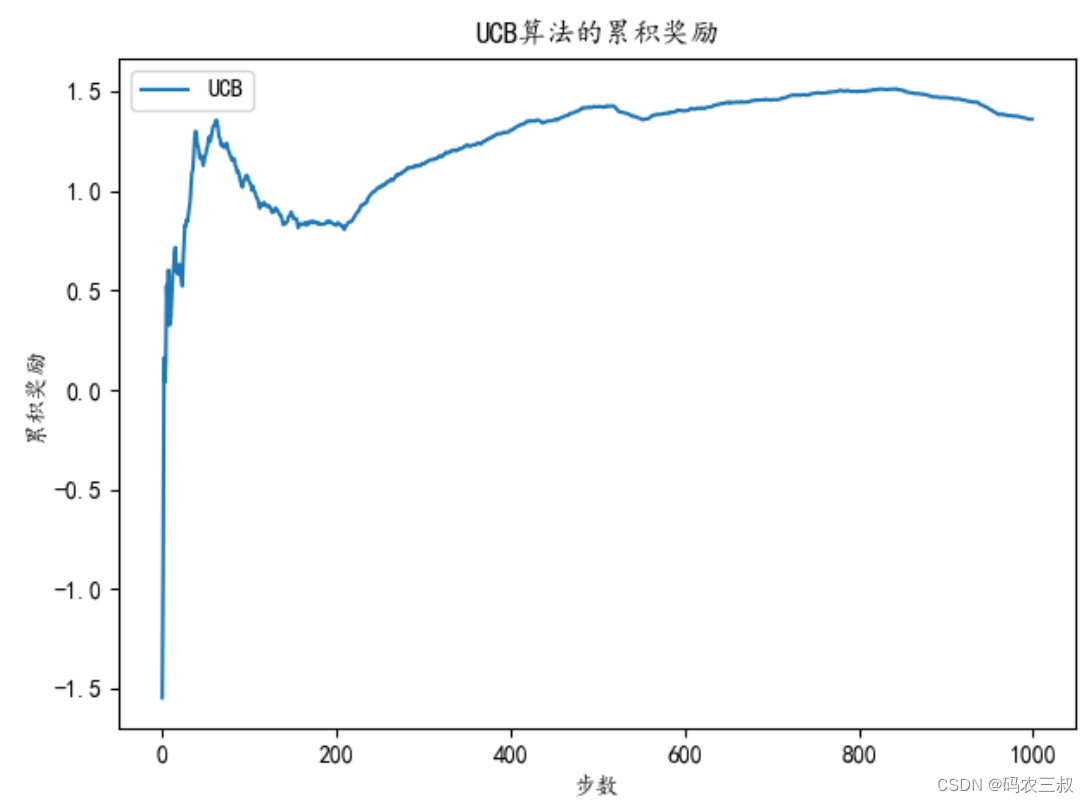

图3-8  累积奖励曲线图

3.3.4  探索策略对蒙特卡洛方法的影响

探索策略对蒙特卡洛方法的影响是一个重要的问题，因为它涉及如何在强化学习任务中平衡探索和利用。蒙特卡洛方法是一种用于估计状态值或动作值的强化学习方法，它通过采样多个回合（trajectories）来估计值函数，然后基于这些估计值来制定策略。影响探索策略的因素有：

1. ε-Greedy 策略：在蒙特卡洛方法中，可以使用 ε-Greedy 策略来平衡探索和利用。ε-Greedy 策略以概率 ε 随机选择动作，以概率 1-ε 选择当前估计最高的动作。ε 的大小决定了探索的程度，较小的 ε 会更倾向于利用当前估计最高的动作，而较大的 ε 会更倾向于探索未知动作。因此，选择合适的 ε 值对蒙特卡洛方法的性能至关重要。
2. 初始值：蒙特卡洛方法的初始值估计可以影响探索策略。如果初始值偏向高估计，算法可能会更早地倾向于利用，而如果初始值偏向低估计，算法可能会更早地倾向于探索。
3. 回合数：蒙特卡洛方法的性能还受到回合数的影响。更多的回合可以提供更多的探索机会，但同时也会增加计算成本。
4. 探索方法：除了ε-Greedy 策略，还可以使用其他探索方法，如 UCB（Upper Confidence Bound）或 Thompson Sampling，这些方法可以更智能地选择探索动作。

总之，探索策略对蒙特卡洛方法的影响取决于任务的性质和问题的复杂性。选择合适的探索策略是蒙特卡洛方法中的关键问题，需要根据具体情况进行调整和优化，以获得更好的性能。例如下面是一个展示探索策略对蒙特卡洛方法影响的例子，在这个示例中定义了一个简单的任务，目标是估计一个状态的真实价值。我们使用蒙特卡洛方法来估计值函数，并尝试不同的 ε 值（探索参数）：0.1、0.2 和 0.5。然后，比较了不同 ε 值对蒙特卡洛方法的影响，并绘制了每个 ε 值下的平均奖励随回合数的变化曲线。

实例3-8：使用不同的ε值影响算法性能（源码路径：daima\3\ying.py）

实例文件ying.py的具体实现代码如下所示。

import numpy as np
import matplotlib.pyplot as plt

# 定义一个简单的蒙特卡洛任务：估计一个状态的真实价值
true_value = 3.0

# 蒙特卡洛方法函数
def monte_carlo_method(num_episodes, epsilon):
    values = np.zeros(num_episodes)  # 存储每个回合的估计值
    for episode in range(num_episodes):
        total_reward = 0.0
        num_steps = 0
        while True:
            if np.random.rand() < epsilon:
                action = np.random.randn()  # 随机探索
            else:
                action = true_value  # 利用当前估计最高的动作
            reward = np.random.normal(true_value, 1.0)  # 模拟获得奖励
            total_reward += reward
            num_steps += 1
            if num_steps >= 100:  # 回合最大长度
                break
        values[episode] = total_reward / num_steps  # 记录每个回合的平均奖励
    return values

# 比较不同 ε 值对蒙特卡洛方法的影响
epsilon_values = [0.1, 0.2, 0.5]
num_episodes = 1000

plt.figure(figsize=(10, 5))
for epsilon in epsilon_values:
    values = monte_carlo_method(num_episodes, epsilon)
    plt.plot(values, label=f"ε = {epsilon}")

plt.xlabel("回合数")
plt.ylabel("平均奖励")
plt.title("探索策略对蒙特卡洛方法的影响")
plt.legend()
plt.show()

对上述代码的具体说明如下：

1. 定义了一个简单的任务，其中有一个状态的真实价值为3.0。
2. 使用蒙特卡洛方法来估计这个状态的真实价值。
3. 通过参数化的 ε-Greedy 策略来探索不同的探索与利用权衡方式，其中 ε 是一个探索参数。
4. 在多个回合中运行蒙特卡洛方法，每个回合中会执行一系列动作和奖励模拟，模拟的奖励服从均值为真实价值的正态分布。
5. 对于每个回合，记录下平均奖励的估计值。
6. 针对不同的 ε 值（0.1、0.2 和 0.5），比较了在相同的回合数下，平均奖励的变化趋势。
7. 最终，通过绘制可视化图，展示了不同ε值下的平均奖励随回合数的变化，以帮助理解探索策略对蒙特卡洛方法的影响。观察图表可以帮助选择适合任务的探索参数，以平衡探索和利用的权衡。

执行后会绘制如图3-8所示的可视化图，展示不同探索参数 (ε) 值对蒙特卡洛方法的影响。我们可以观察到，较小的 ε 值（例如 0.1）倾向于更多地利用当前估计最高的动作，导致估计值收敛较快，但可能错过了更好的动作。较大的 ε 值（例如 0.5）倾向于更多地探索未知动作，导致估计值变化较大，但可能需要更多回合才能收敛到真实价值。选择适当的 ε 值取决于任务的性质和目标。

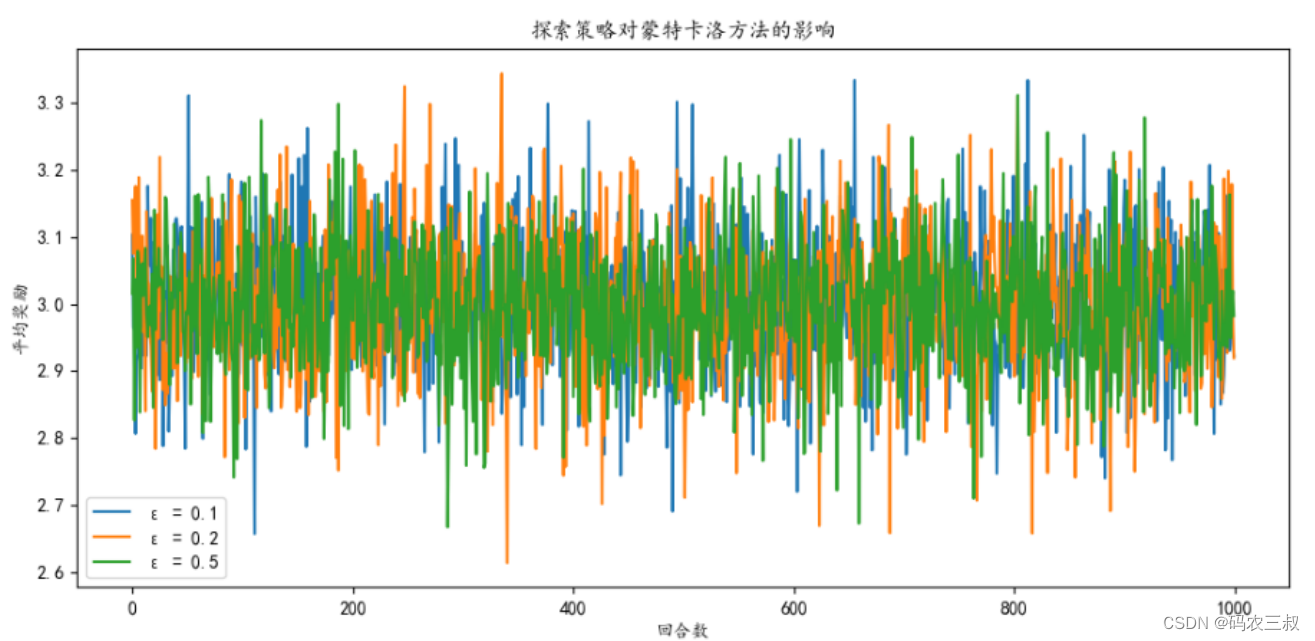
图3-8  不同探索参数 (ε) 值对蒙特卡洛方法的影响折线图

上述不同探索参数 (ε) 值对蒙特卡洛方法的影响折线图包括以下内容：

1. x 轴表示回合数 (Episodes)，即算法运行的回合次数。
2. y 轴表示平均奖励 (Average Reward)，即每个回合的平均奖励值。
3. 图中将包含多条曲线，每条曲线对应一个不同的 ε 值。例如，ε = 0.1、ε = 0.2 和 ε = 0.5。

通过观察这张图可以了解在不同的探索参数下，展示算法的性能如何随着回合数的增加而变化。不同的 ε 值代表不同的探索与利用策略，因此上图可以帮助我们理解探索策略对蒙特卡洛方法的影响，以及如何选择合适的 ε 值来平衡探索与利用。

本《蒙特卡洛方法》专题已完结：

(3-1)蒙特卡洛方法：蒙特卡洛预测-CSDN博客

(3-2)蒙特卡洛方法：蒙特卡洛控制-CSDN博客