基于uwb和IMU融合的三维空间定位算法matlab仿真

最新推荐文章于 2024-09-14 18:02:15 发布

简简单单做算法

最新推荐文章于 2024-09-14 18:02:15 发布

阅读量2k

点赞数 1

分类专栏： MATLAB算法开发 # 通信信号文章标签：算法 matlab uwb IMU融合三维空间定位

本文链接：https://blog.csdn.net/aycd1234/article/details/132768516

版权

MATLAB算法开发同时被 2 个专栏收录

323 篇文章

订阅专栏

通信信号

69 篇文章

订阅专栏

1.算法运行效果图预览

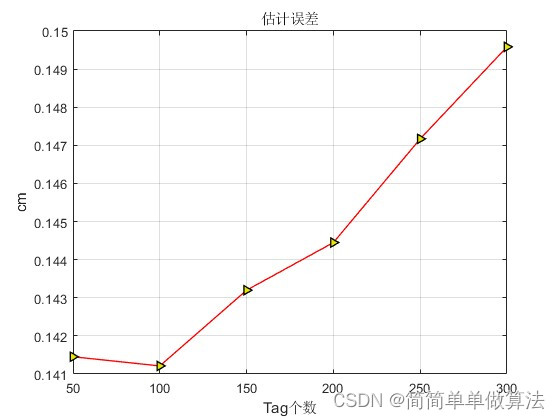
2.算法运行软件版本

matlab2022a

3.部分核心程序

..........................................................................


kkk = 0;
for EbN0 = EbN0_sub
    kkk
    kkk = kkk + 1;
    
    for jj1 = 1:Tag_Num
        jj1
        rng(jj1);
        for jj = 1:num_bits
            
            %TAG to BS1
            delay_1         = round(time_bs_tag(1,jj1)/ts);
            xx1             = zeros(1,delay_1);
            %传播时延
            delay_1_1(jj,:) = [xx1 sig(1:end-length(xx1))];
            %UWB
            h_4             = uwb_channel(dist_bs_tag(1,jj1)); 
            %信号经过信道
            conv_data1      = conv(delay_1_1(jj,:),h_4); 
            UWB_chan1(jj,:) = conv_data1(1:length(sig));
            
            
            
            %TAG to BS2
            delay_2         = round(time_bs_tag(2,jj1)/ts);
            xx2             = zeros(1,delay_2);
            %传播时延
            delay_2_1(jj,:) = [xx2 sig(1:end-length(xx2))];
            h_2             = uwb_channel(dist_bs_tag(2,jj1));
            conv_data2      = conv(delay_2_1(jj,:),h_2);
            UWB_chan2(jj,:) = conv_data2(1:length(sig));

            %TAG to BS3
            delay_3         = round(time_bs_tag(3,jj1)/ts);
            xx3             = zeros(1,delay_3);
            %传播时延
            delay_3_1(jj,:) = [xx3 sig(1:end-length(xx3))];
            h_3             = uwb_channel(dist_bs_tag(3,jj1));
            conv_data3      = conv(delay_3_1(jj,:),h_3);
            UWB_chan3(jj,:) = conv_data3(1:length(sig));

            %TAG to BS4
            delay_4         = round(time_bs_tag(4,jj1)/ts);
            xx4             = zeros(1,delay_4);
            %传播时延
            delay_4_1(jj,:) = [xx4 sig(1:end-length(xx4))];
            h_4             = uwb_channel(dist_bs_tag(4,jj1));
            conv_data4      = conv(delay_4_1(jj,:), h_4);
            UWB_chan4(jj,:) = conv_data4(1:length(sig));   
        end

        for jj = 1:num_bits
            UWB_chan1n(jj,:) = awgn(UWB_chan1(jj,:)/max(UWB_chan1(jj,:)),EbN0,'measured');
            UWB_chan2n(jj,:) = awgn(UWB_chan2(jj,:)/max(UWB_chan2(jj,:)),EbN0,'measured');
            UWB_chan3n(jj,:) = awgn(UWB_chan3(jj,:)/max(UWB_chan3(jj,:)),EbN0,'measured');
            UWB_chan4n(jj,:) = awgn(UWB_chan4(jj,:)/max(UWB_chan4(jj,:)),EbN0,'measured');
        end

        
        %自适应前沿检测
        %自适应前沿检测

..........................................................
        
    end
end


P_est0 = [x_est0',y_est0',z_est0'];
P_est1 = [x_est1',y_est1',z_est1'];

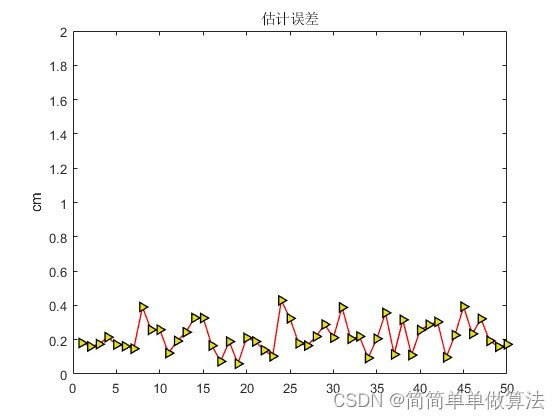
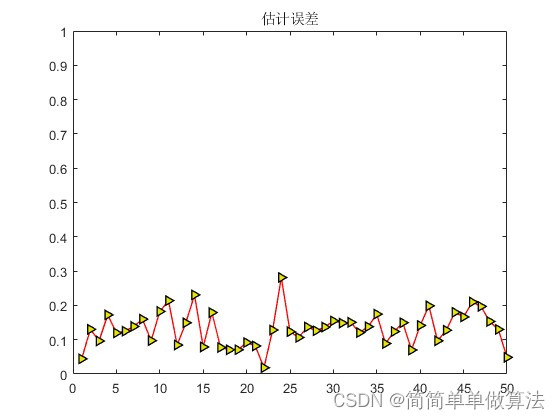
figure;
plot(toa_error0,'-r>',...
    'LineWidth',1,...
    'MarkerSize',6,...
    'MarkerEdgeColor','k',...
    'MarkerFaceColor',[0.9,0.9,0.0]);
 
hold on
title('估计误差')
 
axis([0,Tag_Num,0,2]);
ylabel('cm');


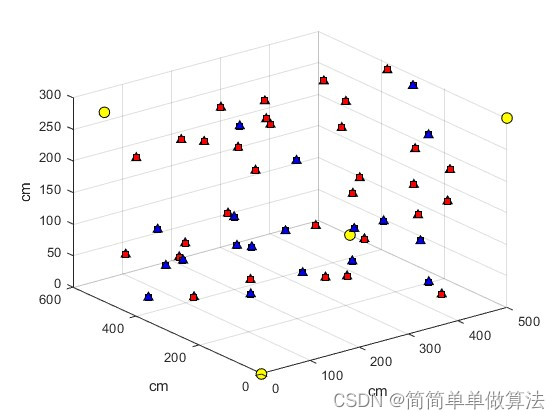
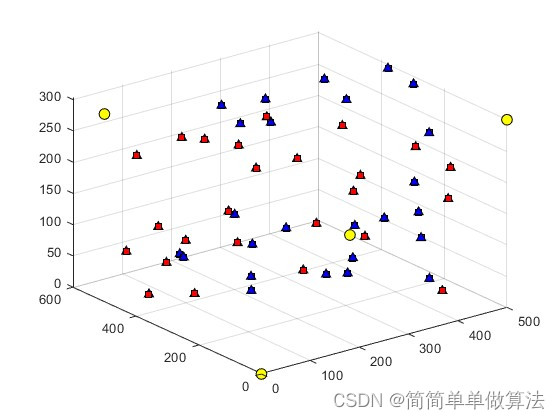
figure
axis([0 10 0 10 0 10]);  
for i=1:BS_Num      
    plot3(BS_pos(i,1),BS_pos(i,2),BS_pos(i,3),'ko','MarkerFace','y','MarkerSize',8);
    hold on
end
hold on
for i=1:Tag_Num
plot3(Tag(i,1),Tag(i,2),Tag(i,3),'k^','MarkerFace','b','MarkerSize',6);
hold on
plot3(x_est1(i),y_est1(i),z_est1(i),'ks','MarkerFace','r','MarkerSize',6);
hold on
end

grid on
xlabel('cm');
ylabel('cm');
zlabel('cm');


save R.mat toa_error1
36_003m

4.算法理论概述

基于UWB和IMU融合的三维空间定位算法是一个结合了无线脉冲波（UWB）和惯性测量单元（IMU）各自优势的定位方法。UWB通过测量信号的传输时间来计算距离，具有精度高、抗干扰能力强等优点，但易受多径效应和环境噪声的影响。IMU则通过测量加速度和角速度来计算姿态和位置信息，具有实时性和动态性强的特点，但受限于加速度的测量误差和漂移。

通过将这两种技术进行融合，可以充分利用它们的优点来提高定位精度和稳定性。具体来说，UWB可以提供高精度的距离信息，用于计算目标的位置和姿态，而IMU可以提供实时的加速度和角速度信息，用于修正UWB的测量误差和漂移，同时提高系统的响应速度和鲁棒性。

下面介绍一种基于UWB和IMU融合的三维空间定位算法，其原理和数学公式如下：

UWB定位

UWB采用双基站的定位方式，假设已知两个基站的位置坐标为(x1, y1, z1)和(x2, y2, z2)，目标的位置坐标为(x, y, z)，则可以通过以下公式计算目标到两个基站的距离差：

Δd = (x2-x1)² + (y2-y1)² + (z2-z1)² - (x-x1)² - (y-y1)² - (z-z1)²

其中，(x, y, z)为目标的位置坐标，(x1, y1, z1)和(x2, y2, z2)分别为两个基站的位置坐标。根据距离差和两个基站的坐标，可以列出两个方程，求解得到目标的位置坐标(x, y, z)。

IMU辅助

IMU可以提供实时的加速度和角速度信息，用于修正UWB的测量误差和漂移。具体来说，IMU可以提供一个加速度传感器和一个陀螺仪，分别测量加速度和角速度信息。通过对这些信息进行积分和平滑处理，可以得到目标的姿态和位置信息。

在融合过程中，可以将IMU的加速度和角速度信息作为UWB的辅助数据，对UWB的测量结果进行修正。具体来说，可以将IMU的加速度信息用于计算目标的速度和加速度，对UWB的距离测量结果进行修正，同时利用IMU的角速度信息对UWB的角度测量结果进行修正。这样可以使系统具有更高的精度和鲁棒性。

融合算法

基于UWB和IMU融合的三维空间定位算法主要包括两个阶段：数据采集阶段和数据融合阶段。在数据采集阶段，通过UWB和IMU采集目标的位置、速度、加速度、角速度等信息；在数据融合阶段，将采集到的数据进行融合处理，得到目标的最终位置、速度、加速度、角速度等信息。
解算过程可以根据需要采用最小二乘法、卡尔曼滤波等方法进行优化求解。例如，采用卡尔曼滤波算法可以将UWB和IMU的数据进行融合处理，得到更为精确的目标位置、速度、加速度、角速度等信息。具体实现过程如下：

（1）初始化状态矩阵和控制矩阵；
（2）通过UWB和IMU采集数据；
（3）利用采集到的数据计算状态矩阵和控制矩阵；
（4）根据卡尔曼滤波公式对状态矩阵和控制矩阵进行迭代计算；
（5）根据迭代结果计算目标的最终位置、速度、加速度、角速度等信息。

算法优点

基于UWB和IMU融合的三维空间定位算法具有以下优点：
（1）精度高：通过UWB和IMU的融合，可以减小环境噪声对定位精度的影响，提高算法的鲁棒性；
（2）实时性强：IMU的加速度和角速度信息可以提供实时的姿态和位置信息，对UWB的距离测量结果进行修正，缩短了系统的响应时间；
（3）可靠性高：通过数据融合技术处理多传感器数据，可以减小单一传感器的故障对系统性能的影响；
（4）扩展性强：该算法可以适用于多种场景，例如机器人定位、无人驾驶等。