最近在做地图相关的项目,研究了一下OpenDRIVE,这篇文章主要记录了OpenDRIVE中的几类线条的实现,分享给大家,希望对大家有所帮助。
OpenDRIVE中主要的线条有以下几种:
- 直线(line)
- 弧线(arc)
- 螺旋线(spiral)
只要有这三类线条便可以画出路的引用线(reference line)。先看一下在Unity中的效果(所用案例地址):
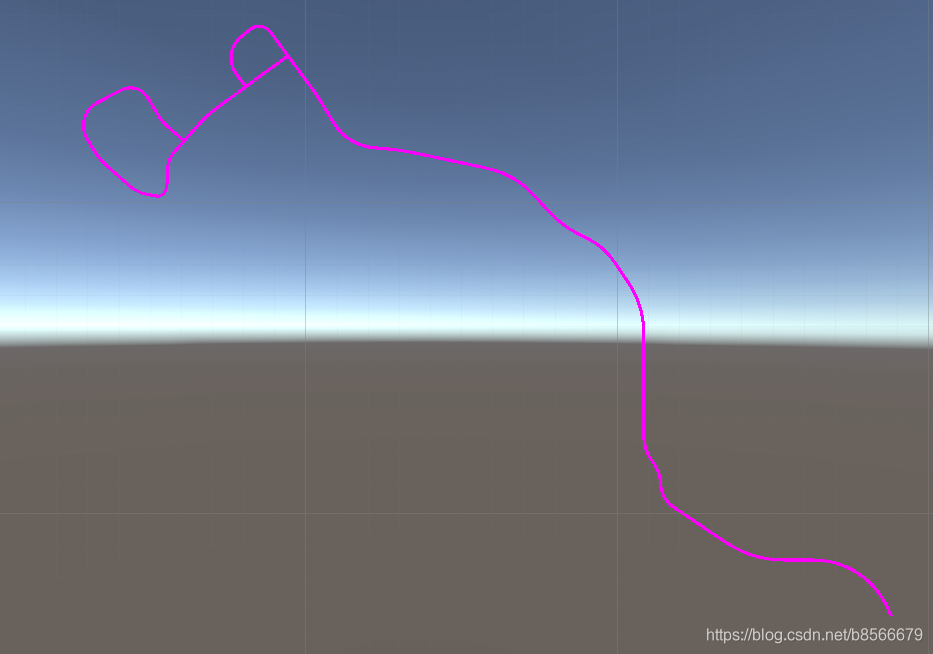
首先根据OpenDRIVE官方文档提供的数据格式,创建出各种线条的类。

文档中所有线条都继承自geometry,所以我们建立LineBase作为基类:
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
[System.Serializable]
public abstract class LineBase
{
public float s;//start position (s-coordinate)
public float x;//start position (x inertial)
public float y;//start position (y inertial)
public float hdg;//start orientation (inertial heading)
public float length;//length of the element's reference line
public LineBase(float s, float x, float y, float heading, float length)
{
this.s = s;
this.y = y;
this.x = x;
this.hdg = heading;
this.length = length;
}
public Vector3 GetPositionAtS(float s)
{
Vector2 v2 = CalculatePoint(s);
Vector3 v3 = new Vector3(v2.x, 0, v2.y);//opendrive的坐标和unity的有区别,需要转换
return v3;
}
protected abstract Vector2 CalculatePoint(float s);
}
-
直线(line):
直线很简单,我们只需要知道起始点坐标x、y和heading轴旋转角度hdg便可以推出在s上的坐标:
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
public class StraightLine : LineBase
{
public StraightLine(float s, float x, float y, float heading, float length) : base(s, x, y, heading, length)
{
}
protected override Vector2 CalculatePoint(float s)
{
var dx = s * Mathf.Cos(hdg);
var dy = s * Mathf.Sin(hdg);
Vector2 startPos = new Vector2(x, y);
return startPos + new Vector2(dx, dy);
}
}
-
弧线(Arc):
弧线多了一个属性:曲率(curvature),根据曲率便可以画出一个弧线:
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
public class ArcLine : LineBase
{
public float curvature;
public ArcLine(float s, float x, float y, float heading, float length,float curvature) : base(s, x, y, heading, length)
{
this.curvature = curvature;
}
protected override Vector2 CalculatePoint(float s)
{
var c = curvature;
var hd = hdg - Mathf.PI / 2;
var a = 2 / c * Mathf.Sin(s * c / 2);
var alpha = (Mathf.PI - s * c) / 2 - hd;
var dx = -1 * a * Mathf.Cos(alpha);
var dy = a * Mathf.Sin(alpha);
Vector2 startPos = new Vector2(x, y);
return startPos + new Vector2(dx, dy);
}
}
-
螺旋线(Spiral)
螺旋线是比较复杂同时也是运用场景非常多的一种曲线,具体介绍可以自行搜索。
关键属性:curvStart(螺旋线开始的曲率)、curvEnd(螺旋线结束时的曲率)
代码参考资料:
https://github.com/liuyf5231/opendriveparser
http://opendrive.org/tools/odrSpiral.zip
using System;
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
public class SpiralLine : LineBase
{
public float cDot;
public float curvStart;
public float curvEnd;
/// <summary>
///
/// </summary>
/// <param name="heading"></param>
/// <param name="length"></param>
/// <param name="cDot">first derivative of curvature [1/m2]</param>
public SpiralLine(float s, float x, float y, float heading, float length, float curvStart, float curvEnd) : base(s, x, y, heading, length)
{
this.curvStart = curvStart;
this.curvEnd = curvEnd;
this.cDot = (curvEnd - curvStart) / length;// curvStart;
}
System.Numerics.Complex j1 = new System.Numerics.Complex(0, 1);
protected override Vector2 CalculatePoint(float s)
{
var c0 = x + j1 * y;
System.Numerics.Complex cs;
if (cDot == 0 && curvStart == 0)
{
cs = c0 + System.Numerics.Complex.Exp(j1 * hdg * s);
}
else if (cDot == 0 && curvStart != 0)
{
cs = c0 + System.Numerics.Complex.Exp(j1 * cDot) / curvStart * (
Math.Sin(curvStart * s) + j1 * (1 - Math.Cos(curvStart * s)));
}
else
{
cs = _calc_fresnel_integral(s, curvStart, hdg, c0);
}
return new Vector2((float)cs.Real, (float)cs.Imaginary);
}
System.Numerics.Complex _calc_fresnel_integral(float s, float kappa0, float theta0, System.Numerics.Complex C0)
{
double sa = 0, ca = 0;
fresnel((kappa0 + cDot * s) / Math.Sqrt(Math.PI * Math.Abs(cDot)), ref sa, ref ca);
double sb = 0, cb = 0;
fresnel(kappa0 / Math.Sqrt(Math.PI * Math.Abs(cDot)), ref sb, ref cb);
var cs1 = Math.Sqrt(Math.PI / Math.Abs(cDot)) * System.Numerics.Complex.Exp(
j1 * (theta0 - kappa0 * kappa0 / 2 / cDot)
);
var cs2 = Math.Sign(cDot) * (ca - cb) + j1 * sa - j1 * sb;
var cs = C0 + cs1 * cs2;
return cs;
}
#region
/* S(x) for small x */
static double[] sn = new double[] {
-2.99181919401019853726E3,
7.08840045257738576863E5,
-6.29741486205862506537E7,
2.54890880573376359104E9,
-4.42979518059697779103E10,
3.18016297876567817986E11,
};
static double[] sd = {
/* 1.00000000000000000000E0,*/
2.81376268889994315696E2,
4.55847810806532581675E4,
5.17343888770096400730E6,
4.19320245898111231129E8,
2.24411795645340920940E10,
6.07366389490084639049E11,
};
/* C(x) for small x */
static double[] cn = {
-4.98843114573573548651E-8,
9.50428062829859605134E-6,
-6.45191435683965050962E-4,
1.88843319396703850064E-2,
-2.05525900955013891793E-1,
9.99999999999999998822E-1,
};
static double[] cd = {
3.99982968972495980367E-12,
9.15439215774657478799E-10,
1.25001862479598821474E-7,
1.22262789024179030997E-5,
8.68029542941784300606E-4,
4.12142090722199792936E-2,
1.00000000000000000118E0,
};
/* Auxiliary function f(x) */
static double[] fn = {
4.21543555043677546506E-1,
1.43407919780758885261E-1,
1.15220955073585758835E-2,
3.45017939782574027900E-4,
4.63613749287867322088E-6,
3.05568983790257605827E-8,
1.02304514164907233465E-10,
1.72010743268161828879E-13,
1.34283276233062758925E-16,
3.76329711269987889006E-20,
};
static double[] fd = {
/* 1.00000000000000000000E0,*/
7.51586398353378947175E-1,
1.16888925859191382142E-1,
6.44051526508858611005E-3,
1.55934409164153020873E-4,
1.84627567348930545870E-6,
1.12699224763999035261E-8,
3.60140029589371370404E-11,
5.88754533621578410010E-14,
4.52001434074129701496E-17,
1.25443237090011264384E-20,
};
/* Auxiliary function g(x) */
static double[] gn = {
5.04442073643383265887E-1,
1.97102833525523411709E-1,
1.87648584092575249293E-2,
6.84079380915393090172E-4,
1.15138826111884280931E-5,
9.82852443688422223854E-8,
4.45344415861750144738E-10,
1.08268041139020870318E-12,
1.37555460633261799868E-15,
8.36354435630677421531E-19,
1.86958710162783235106E-22,
};
static double[] gd = {
/* 1.00000000000000000000E0,*/
1.47495759925128324529E0,
3.37748989120019970451E-1,
2.53603741420338795122E-2,
8.14679107184306179049E-4,
1.27545075667729118702E-5,
1.04314589657571990585E-7,
4.60680728146520428211E-10,
1.10273215066240270757E-12,
1.38796531259578871258E-15,
8.39158816283118707363E-19,
1.86958710162783236342E-22,
};
static double polevl(double x, double[] coef, int n)
{
double ans;
double[] p = coef;
int i;
//ans = *p++;
ans = p[0];
i = n;
int index = 1;
do
{
ans = ans * x + p[index];
index++;
}
while (--i > 0);
return ans;
}
static double p1evl(double x, double[] coef, int n)
{
double ans;
double[] p = coef;
int i;
//ans = x + *p++;
ans = x + p[0];
i = n - 1;
int index = 1;
do
{
ans = ans * x + p[index];
index++;
}
while (--i > 0);
return ans;
}
static void fresnel(double xxa, ref double ssa, ref double cca)
{
double f, g, cc, ss, c, s, t, u;
double x, x2;
x = Math.Abs(xxa);
x2 = x * x;
if (x2 < 2.5625)
{
t = x2 * x2;
ss = x * x2 * polevl(t, sn, 5) / p1evl(t, sd, 6);
cc = x * polevl(t, cn, 5) / polevl(t, cd, 6);
}
else if (x > 36974.0)
{
cc = 0.5;
ss = 0.5;
}
else
{
x2 = x * x;
t = Math.PI * x2;
u = 1.0 / (t * t);
t = 1.0 / t;
f = 1.0 - u * polevl(u, fn, 9) / p1evl(u, fd, 10);
g = t * polevl(u, gn, 10) / p1evl(u, gd, 11);
t = Math.PI * 0.5 * x2;
c = Math.Cos(t);
s = Math.Sin(t);
t = Math.PI * x;
cc = 0.5 + (f * s - g * c) / t;
ss = 0.5 - (f * c + g * s) / t;
}
if (xxa < 0.0)
{
cc = -cc;
ss = -ss;
}
cca = cc;
ssa = ss;
}
/**
* compute the actual "standard" spiral, starting with curvature 0
* @param s run-length along spiral
* @param cDot first derivative of curvature [1/m2]
* @param x resulting x-coordinate in spirals local co-ordinate system [m]
* @param y resulting y-coordinate in spirals local co-ordinate system [m]
* @param t tangent direction at s [rad]
*/
public static void odrSpiral(double s, double cDot, ref double x, ref double y, ref double t)
{
double a;
a = 1.0 / Math.Sqrt(System.Math.Abs(cDot));
a *= Mathf.Sqrt(Mathf.PI);
fresnel(s / a, ref y, ref x);
x *= a;
y *= a;
if (cDot < 0.0)
y *= -1.0;
t = s * s * cDot * 0.5;
}
#endregion
public override string ToString()
{
return string.Format("x:{0} y:{1} heading:{2} length:{3} s:{4}", x, y, hdg, length,s);
}
}
其它文件:OpenDRIVE完整数据格式C#版
来自:刘一码的原创

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








