诱导公式的本质【转载】

利用单位圆定义了三角比，而单位圆又具有很好的对称性，这些对称的性质产生了诱导公式。诱导公式可以不用记忆，用的时候直接画单位圆观察对称性即可。比如：

• 角π+α的终边与角α的终边关于原点中心对称
  
• 角π-α的终边与角α的终边关于y轴对称
  
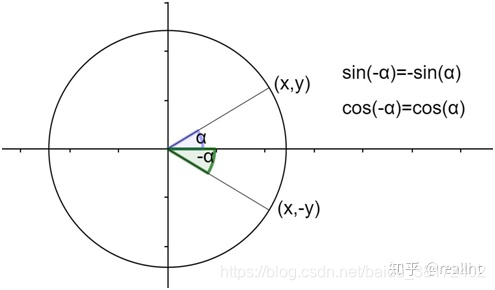
• 角-α的终边与角α的终边关于x轴对称
  
• 角π/2-α的终边与角α的终边关于直线y=x对称
  

注意：此图有误，π/2-α的终边的坐标应为(y,x)

• 角π/2+α的终边三角形与角α的终边三角形全等
  
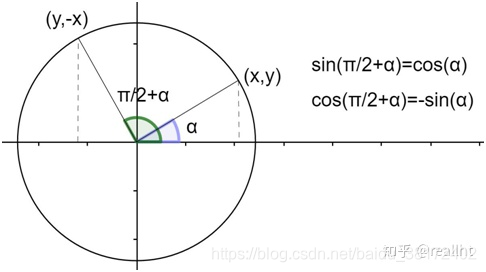
  关于口诀“奇变偶不变，符号看象限
• 奇变偶不变，主要针对$\frac{K\pi }{2}\pm \alpha$与$\alpha$之间的关系，这里必须把$\alpha$看作锐角，当$K$为奇数是发生改变，偶数则不发生改变。符号看$\frac{K\pi }{2}\pm \alpha$所位于的坐标象限。

---

以上内容来自：

• realht_诱导公式的本质【知乎】