MIT 18.06 linear algebra lecture 16 投影矩阵和最小二乘 笔记

投影

上一节提到投影矩阵\(P=A(A^TA)^{-1}A^T\)能将\(\boldsymbol{b}\)投影到\(A\)的列空间上。如果\(\boldsymbol{b}\)垂直于列空间，则\(\boldsymbol{b}\)在左零空间\(N(A^T)\)中，并且\(P\boldsymbol{b}=\boldsymbol{0}\)；如果\(\boldsymbol{b}\)在列空间中，则\(\boldsymbol{b}=A\boldsymbol{x}\)，且\(P\boldsymbol{b}=\boldsymbol{b}\)。

一般情况下，一个向量\(\boldsymbol{b}\)通常有一部分\(\boldsymbol{p}\)在列空间中，另一部分\(\boldsymbol{e}\)与列空间垂直（在左零空间中），\(\boldsymbol{b}\)的投影即是在列空间的那一部分\(\boldsymbol{p}\)。
将\(\boldsymbol{b}\)投影到左零空间\(N(A^T)\)的矩阵是\(I-P\)：
\[ \begin{aligned} \boldsymbol{e}&=\boldsymbol{b}-\boldsymbol{p}\\ \boldsymbol{e}&=(I-P)\boldsymbol{b} \end{aligned} \]

最小二乘

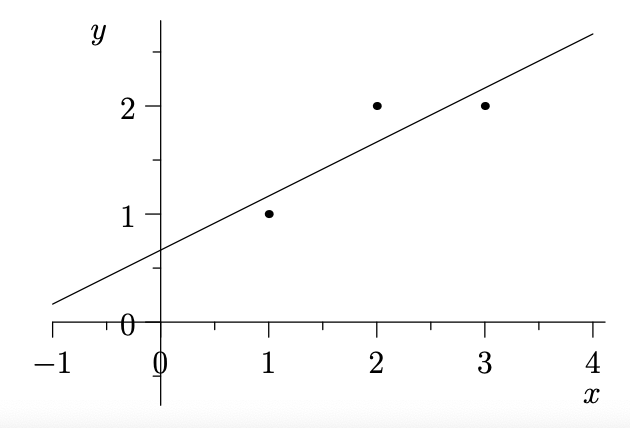
接着上一节的内容，找到离点\((1,1)\)、\((2,2)\)和\((3,2)\)最近的直线\(b=C+Dt\)。通常称这个过程是线性回归（linear regression），当数据点没有异常点（outliers）的时候，该技术还是非常有效的。
最近的直线意味着，能够最小化点到直线距离的误差。通过将距离的平方加起来，换句话说，希望最小化\(\|A\boldsymbol{x}-\boldsymbol{b}\|=\|\boldsymbol{e}\|^2\)

如果直线通过三个点，有：
\[ \begin{aligned} C+D&=1\\ C+2D&=2\\ C+3D&=2 \end{aligned} \]
但是该方程组是无解的，等价于\(A\boldsymbol{x}=\boldsymbol{b}\)，其中：
\[ A= \begin{bmatrix} 1&1\\ 1&2\\ 1&3 \end{bmatrix}, \boldsymbol{x}= \begin{bmatrix} C\\ D \end{bmatrix}\text{ and }\boldsymbol{b}= \begin{bmatrix} 1\\ 2\\ 2 \end{bmatrix} \]
可以从两种角度看待，在直线空间中\(e_1\)、\(e_2\)和\(e_3\)是数据点到直线的垂直距离，\(p_1\)、\(p_2\)和\(p_3\)是\(C+Dt\)上靠近数据点的值：\(\boldsymbol{b}\approx \boldsymbol{p}\)。
另一种角度，考虑到\(\boldsymbol{b}\)在\(\mathbb{R}^3\)中，投影\(\boldsymbol{p}\)在\(A\)的列空间中，投影\(\boldsymbol{e}\)在\(N(A^T)\)中。
接下来求解\(\hat{\boldsymbol{x}}=\begin{bmatrix}\hat{C}\\\hat{D}\end{bmatrix}\)和 \(\boldsymbol{p}\),有：
\[ \begin{aligned} A^TA\hat{\boldsymbol{x}}&=A^T\boldsymbol{b}\\ \left[\begin{array}{rr} 3 & 6\\ 6 & 14 \end{array}\right] \left[\begin{array}{r} \hat{C}\\ \hat{D} \end{array}\right]&= \left[\begin{array}{r} 5\\ 11 \end{array}\right] \end{aligned} \]
通过这个能够得到正规方程（normal equation）：
\[ \begin{aligned} 3\hat{C}+6\hat{D}&=5\\ 6\hat{C}+14\hat{D}&=11 \end{aligned} \]
通过求解正规方程得到解，\(\hat{D}=1/2\)，\(\hat{C}=2/3\)。
除了用线性代数的方法，也能通过使用微积分找到下面式子的最小值：
\[ e_1^2+e_2^2+e_3^2=(C+D-1)^2+(C+2D-2)^2+(C+3D-2)^2 \]
最终找到的离数据点最近的直线是\(b=\frac{2}{3}+\frac{1}{2}t\)

\(i\)	\(p_i\)	\(e_i\)
\(1\)	\(7/6\)	\(-1/6\)
\(2\)	\(5/3\)	\(1/3\)
\(3\)	\(13/6\)	\(-1\)/6

或者\(\boldsymbol{p}=\left[\begin{array}{r}7/6\\5/3\\13/6\end{array}\right]\)和\(\boldsymbol{e}=\left[\begin{array}{r}-1/6\\2/6\\-1/6\end{array}\right]\)。注意到\(\boldsymbol{p}\)和\(\boldsymbol{e}\)是正交的，\(\boldsymbol{e}\)同样垂直于\(A\)的列。

矩阵\(A^TA\)

在上一节的计算过程中，假设了矩阵\(A^TA\)是可逆的，这个假设是否正确呢？接下来证明。

如果\(A\)的列是线性无关的，则\(A^TA\)是可逆的。

如果\(A^TA\boldsymbol{x}=\boldsymbol{0}\)仅在\(\boldsymbol{x}=\boldsymbol{0}\)时成立，则\(A^TA\)是可逆的：
\[ \begin{aligned} A^TA\boldsymbol{x}&=\boldsymbol{0}\\ \boldsymbol{x}^TA^TA\boldsymbol{x}&=\boldsymbol{x}^T\boldsymbol{0}\\ (A\boldsymbol{x})^T(A\boldsymbol{x})&=\boldsymbol{0}\\ A\boldsymbol{x}&=\boldsymbol{0} \end{aligned} \]
因为\(A\)的列是线性无关的，所以\(A\boldsymbol{x}=\boldsymbol{0}\)仅在\(\boldsymbol{x}=\boldsymbol{0}\)时成立。

只要\(A\)的列是线性无关的，可以利用线性回归去找到不可解的线性方程的近似解。当\(A\)的列是标准正交（orthonormal），也是线性无关的。标准正交意味着\(A\)的列是互相垂直的单位向量，如\(\left[\begin{array}{r}1\\0\\0\end{array}\right]\)，\(\left[\begin{array}{r}0\\1\\0\end{array}\right]\)和\(\left[\begin{array}{r}0\\0\\1\end{array}\right]\)或者\(\left[\begin{array}{r}\cos{\theta}\\\sin{\theta}\end{array}\right]\)和\(\left[\begin{array}{r}-\sin{\theta}\\\cos{\theta}\end{array}\right]\)。

---

笔记来源：MIT 18.06 lecture 16

转载于:https://www.cnblogs.com/yuyin/articles/10111712.html