1.1 简单指数平滑
“simple exponential smoothing” (SES)
SES适用于不计趋势与季节性的时间序列
我们在可以使用平均值模型和naive模型来做粗略的预测(点击查看),他们懂预测方法分别是
- 使用最后一个值(naive模型)
- 使用前面值的平均数(平均值)
这里的简单指数平滑是用的前面几个值的加权平均数,越靠近最后的权重越大,后面的权重指数下降
SES的公式如下
y^T+1|T=αyT+α(1−α)yT−1+α(1−α)2yT−2+⋯
α 就是平滑指数,值越大越忽略距离远的数值。
还可以写成以下形式:、
y^t+1|t=αyt+(1−α)y^t|t−1
其中第一个的值的计算公式如下:
y^2|1=αy1+(1−α)ℓ0
我们可以发现这样的问题:其中的 ℓ0 与 α 的值怎么选取最好?
通常的简单做法直接把 ℓ0 设置为y0。
这里我们可以借鉴最小二乘法的方法,通过求解SSE(sum of the squared errors)求最佳参数。
下图显示了不同参数时的SSE值,其中最后一个是通过求解SSE最小值得到的
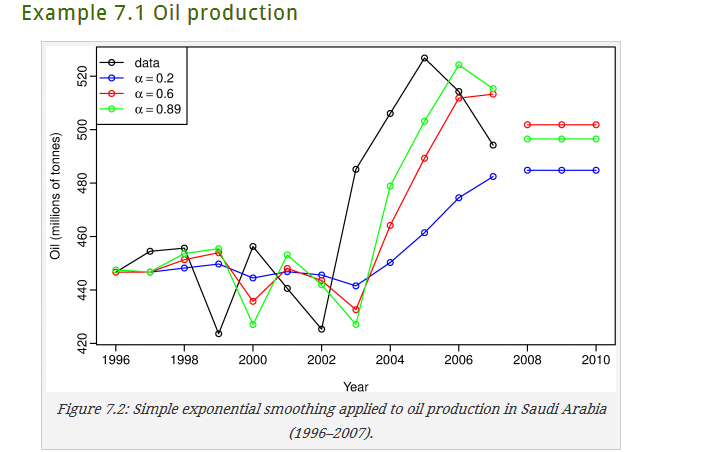
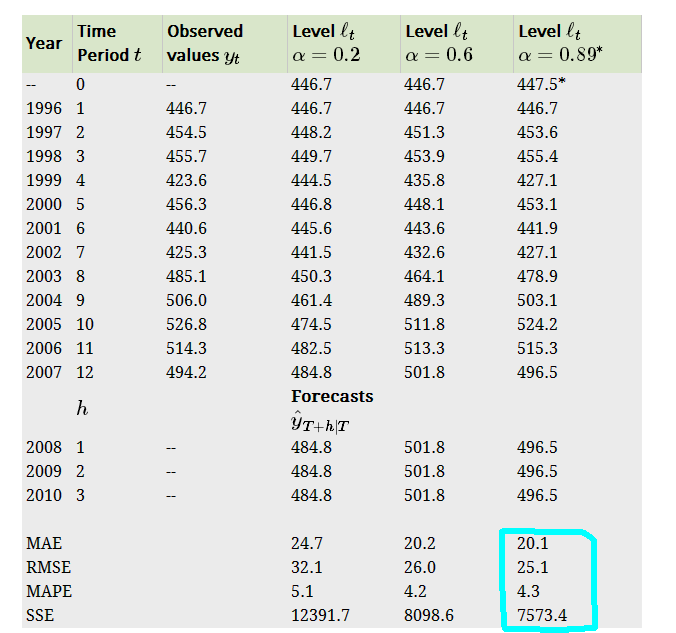
由此可以看出简单指数平滑初步的可以选择了拟合较好的值来预测,比起最初的简单模型要更加合理
1.2 霍尔特线性趋势预测 Holt’s linear trend method
前面的简单指数平滑只能预测一个相同的值,不能有趋势,可以进行一定的线性预测,Holt将其进行了改进,加入了二次平滑,其公式如下:
Forecast equationLevel equationTrend equationyt+h|tℓtbt=ℓt+hbt=αyt+(1−α)(ℓt−1+bt−1)=β∗(ℓt−ℓt−1)+(1−β∗)bt−1
其中b是斜率,其中包含的迭代公式就是第二次平滑。
同样其参数的确定可以根据SSE来计算
sse公式
ℓtbt=ℓt−1+bt−1+αet=bt−1+αβ∗et
et=yt−(ℓt−1+bt−1)=yt−yt|t−1
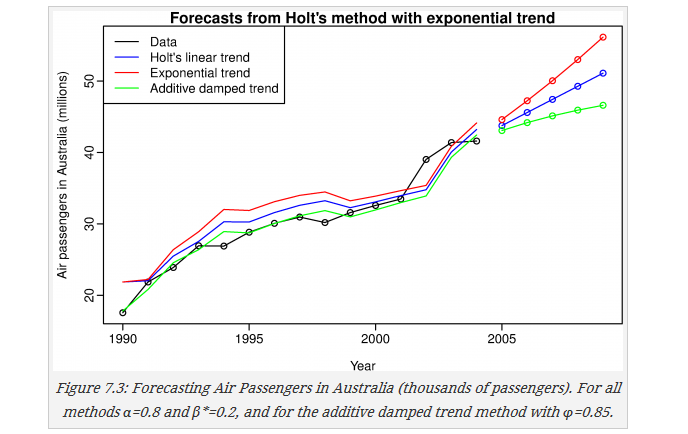
如果其预测值可以有限性趋势,图中其他方法将在后续介绍
1.3 指数趋势预测法Exponential trend method
该方法是将线性趋势中的斜率又一个加数变为了一个乘数因子,公式如下:
y








 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 717
717

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








