时间序列 R 07 时间序列分解 Time series decomposition

一个时间序列可以分解为多个模型的组合

1.1 时间序列的组成

1.1.1 时间序列组成模式

三种时间序列模式（不计剩余残差部分）
1. 趋势Tend ：比如线性趋势，先增加后降低的整体趋势
2. 季节性Seasonal ：以时间为固定周期，呈现循环的特性
3. 周期性Cyclic：在以不固定周期不断震荡，通常周期性至少持续2年
下图就是讲时间序列分解之后的结果，应该比较容易理解上面的定义

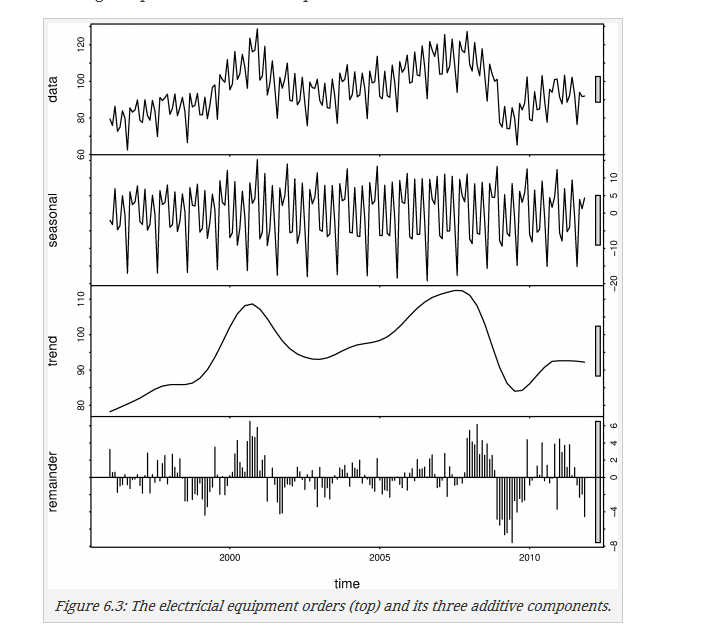
下图是周期性的表现之一：

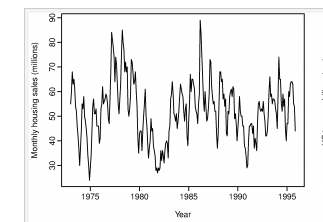
每个周期的震荡持续了6-10年，整体没有什么明显的趋势，第一幅图中trend包含了trend与cyclic

1.1.2 时间序列分解

可以将时间序列按下式分解为上面的几种模式，分解方式有相加方式或者相乘的方式如下：

$$y_{t} = S_{t} + T_{t} + E_{t},$$
或者
$$y_{t} = S_{t} \times T_{t} \times E_{t}.$$
其中 $S_{t}$为季节性模式部分， $T_{t}$为包含趋势与周期性的模式部分， $E_{t}$为剩余残差部分
其各自的适用范围：
- 季节性和trend-cycle变动的量级不随时间变化，用加法模式
- 两者的波动随时间成比例，适用于乘法模式
- 乘法模式可以通过log变为加法模式： $$y_{t} = S_{t} \times T_{t} \times E_{t} \quad \Longleftrightarrow\quad \log y_{t} = \log S_{t} + \log T_{t} + \log E_{t}$$
还是看这幅图

注意右边有一个灰色的比例条，他表示同样尺寸的线段在不同图上的比例，上图可见残差的长度较小。
下面介绍几种图;
1. seasonal sub-series plots

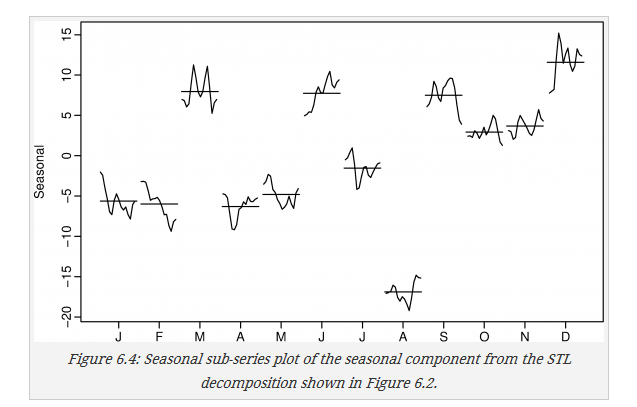
将每个seasonal里面的子周期呈现
2. Seasonally adjusted data
不考虑seasonal的数据

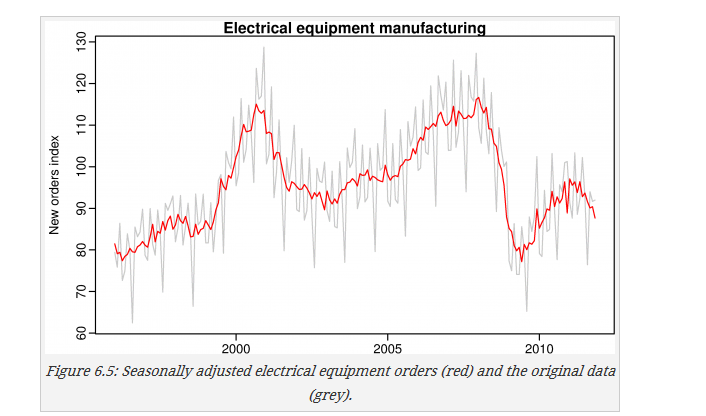
1.2 Moving averages 移动平均

移动平均用于估计时间序列的趋势和周期

1.2.1 Moving average smoothing

简单来说就是用数值前后k个时间点的值的平均值来代替当时值

T^t=1m∑j=−k