卡尔曼滤波的解释

转自：
https://www.jianshu.com/p/d3b1c3d307e0

卡尔曼滤波在我当学生的时候就用过，但是当年我似乎就是套公式，没有理解其精髓，加之时间久了有点模糊，突然需要指导学生使用，有了强烈的陌生感觉，不得不逼自己再一次捡起。自己学会和教会别人是学习的两个层次，为了自我提高，也为了更好得指导学生。于是，我又翻出自己当年写的算法以及在网上找了些大神写的资料，进行融会贯通，总结提炼，希望稍微有点大学概率论的人能够看懂此文并熟练使用。

为了可以更加容易得理解卡尔曼滤波器，我们先回顾了基础的数学知识，然后采用形象的描述方法来讲解其算法本质，接着利用数学符号抽象出数学公式并进行归纳总结，最后给出计算机程序实现。希望初学者从头看到尾，循序渐进，具有较好数学功底者可直接看数学公式，实用主义者可直接拷贝源代码。

1．卡尔曼与其提出的滤波器

在学习卡尔曼滤波器之前，先搞懂“卡尔曼”是什么鬼？其实卡尔曼是人，而且还是一个现代的牛人！卡尔曼全名Rudolf Emil Kalman，匈牙利数学家，1930年出生于匈牙利首都布达佩斯。1953，1954年于麻省理工学院分别获得电机工程学士及硕士学位。1957年于哥伦比亚大学获得博士学位。

我们现在要学习的卡尔曼滤波器，正是源于他的博士论文和1960年发表的论文《A New Approach to Linear Filtering and Prediction Problems》(线性滤波与预测问题的新方法)。写到这我默默流泪，为啥我的论文写完后连自己都不想在看呢？

简单来说，卡尔曼滤波器是一个“optimal recursive data processing algorithm（最优化自回归数据处理算法）”。对于解决很大部分的问题，他是最优，效率最高甚至是最有用的。他的广泛应用已经超过30年，包括机器人导航，控制，传感器数据融合甚至在军事方面的雷达系统以及导弹追踪等等。近年来更被应用于计算机图像处理，例如人脸识别，图像分割，图像边缘检测等等。

2.基础数学知识准备

在正式开讲前，我们需要回顾下数学基础知识，准确的说是概率论的知识。

概率论里，每一个随机变量X都是具有一个平均值（这个值在变量的概率密度函数分布图的最中心位置，代表该数值是最可能发生的）和方差（这个数值代表变量的不确定性程度）。平均值μ就是数学期望μ=E(X)。方差D(X)=σ^2=E{[x-E(x)]2}是衡量随机变量或一组数据时离散程度的度量。方差的平方根即标准差或者均方差，即σ。

那么，一谈到概率统计，我们马上可以想到：两个变量是否相互独立，或者互不相关。相互独立是已知其中一个变量的变换规律，我们无法推断出另外一个变量的变化规律，否者就相互不独立。例如，根据牛顿公式测量的速度和位移随机变量就是相关的。那么相关的程度我们可以用协方差来描述，数学表述为：

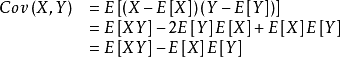
人们总结随机变量的概率分布，可得到一些典型的分布，比如均匀分布、泊松分布和高斯分布等。其中高斯分布，也称正态分布，又称常态分布，是我们常见的分布，记为N（μ，σ^{2），其中μ，σ}2为分布的参数，分别为高斯分布的期望和方差。当有这两者确定值时，概率p(x)也就确定了，特别当μ=0，σ^2=1时，X的分布为标准正态分布。

我们考察单随机变量的高斯分布，其概率密度函数为：

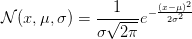
如果存在两个高斯分布，当两个分布相乘时，得到什么结果？（推导过程感兴趣的童鞋可以看随机过程一书）：

结论就是两正态分布的乘积仍然是正态分布，且新正态分布的均值和方差如下：

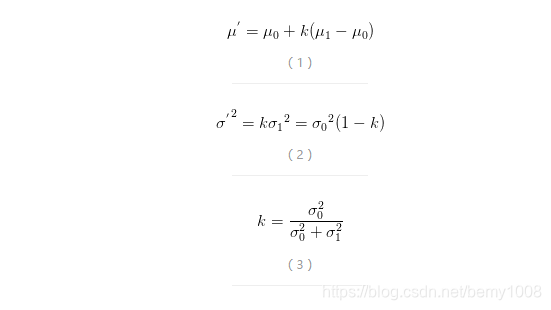
以上是单变量概率密度函数的计算结果，如果是多变量的，那么，就变成了协方差矩阵的形式：

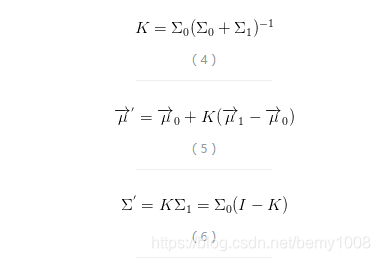
3.卡尔曼滤波的通俗理解

讲解了随机变量和概率，那么为啥要引入卡尔曼滤波呢。卡尔曼滤波适用于估计一个由随机变量组成的动态系统的最优状态。即便是观测到的系统状态参数含有噪声，观测值不准确，卡尔曼滤波也能够完成对状态真实值的最优估计。

为了更好理解为啥需要卡尔曼滤波，我们还是举个实际的例子说明。

考虑轨道上的一个小车，无外力作用。为了便于对它进行控制，需要知道它的位置以及移动速度。所以，建立一个向量，用来存储小车的位置和速度：x(t)=(p,v)，此时位置和速度两者都为随机变量，才为二维随机向量，后面举例会简化为一维，只有位置是随机变量。一个系统的状态有很多，选择最关心的状态来建立这个状态向量是很重要的。例如，状态还有水库里面水位的高低、炼钢厂高炉内的温度、平板电脑上面指尖触碰屏幕的位置等等这些需要持续跟踪的物理量。对于小车我们就采用位置和速度来描述，它在时刻t的状态向量x(t)只与x(t-1)相关：比如：x(0)表示小车在t=0时刻的状态是：速度大小5m/s,速度方向右,位置坐标0。反正有了这个向量就可以完全预测t=1时刻小车的状态。

因为X(t)=Fx(t-1)，那么根据t=0时刻的初值x(0)，理论上我们可以求出它任意时刻的状态。当然，实际情况不会这么美好。这个递推函数可能会受到各种不确定因素的影响（内在的，小车结构不紧密，轮子不圆等，外在的，比如刮风，下雨，地震等）导致x(t)并不能精确标识小车实际的状态。我们假设每个状态分量受到的不确定因素都服从正态分布。

如上所述，状态向量是有维度的。其实如果是一维的卡尔曼滤波很容易说清楚，不比最小二乘法复杂多少。如果涉及多维就没有那么容易理解，因为被抽象为矩阵的形式。对，就是矩阵，一个和线性代数相关的概率，如需要了解多维卡尔曼滤波，请大家自行脑补。

我们首先看最简单的一维情况：假设小车速度均值为2cm/s，我们只用位置表示小车的状态，即只对小车位置进行估计。此时把二维向量简化为标量。

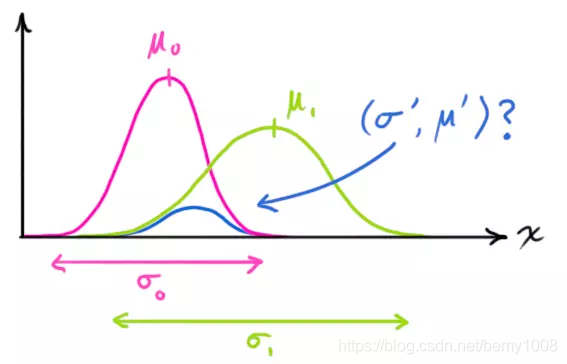
请看下图：t=k-1时小车的位置服从红色的正态分布。假设位置在21cm，位置误差为0.3cm，即μ=21，σ=0.3。

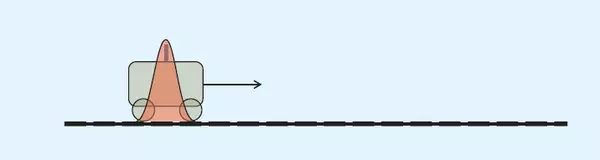
根据小车的这个位置，我们可以根据位置与速度经验公式，预测出t=k时刻它的位置：位置均值是21+2=23cm，我对自己速度预测不确定度为0.4cm，那么此时小车位置预测误差为0.5cm（0.5是这样得到的：如果k-1时刻估算出的最优位置的偏差是0.3，你对自己预测的不确定度是0.4，他们平方相加再开方，就是0.5，为什么是这样？用了正态分布的线性叠加定理，即位置和速度两正态分布的和也满足正态分布，方差是二者平方 ）。可以看出0.5>0.3，此时分布变“胖”了，这很好理解——因为在递推的过程中又加了一层噪声（即预测不稳定度），所以不确定度变大了。

为了避免纯估计带来的偏差，我们在t=k时刻对小车的位置坐标进行一次雷达测量，当然雷达对小车距离的测量也会受到种种因素的影响，会带来测量误差，这个测量误差的均方差是0.4cm，假设此时测量值是25cm(即均值为25)。而且测量结果也复合正态分布，于是可以画出小车在t=1时的位置服从蓝色分布。

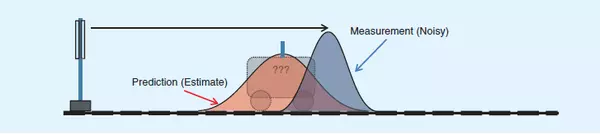
好了，现在我们得到两个不同的结果。那么哪个才是更加可靠的小车现在的位置呢？有人提过加权，那么怎么加权才科学呢？

大家读到这里心里非常清楚的一点是：两个事件的发生都是概率性的，不能完全相信其中的任何一个！如果我们具有两个事件，从直觉或者是理性思维上讲，是不是认定两个事件都发生，就找到了那个最理想的估计值？好了，抽象一下，得到：两个事件同时发生的可能性越大，我们越相信它！要想考察它们同时发生的可能性，就是将两个事件单独发生的概率相乘。于是乎，卡尔曼滤波的思想诞生了！Kalman老先生的牛逼之处就在于找到了相应权值，使红蓝分布合并为下图这个绿色的正态分布。

你问我kalman为什么牛逼？那是因为人家在理论上证明了：绿色分布不仅保证了在红蓝给定的条件下，小车位于该点的概率最大，而且，它居然还是一个正态分布！正态分布就意味着，可以把它当做初值继续往下算了！这是Kalman滤波能够迭代的关键。

由于我们用于估算k时刻的实际位置有两个位置值，分别是23cm和25cm。究竟实际位置是多少呢？相信自己预测还是相信雷达测量呢？究竟相信谁多一点，我们可以用kalman的方法来加权，即利用他们的方差σ^2来判断，求出绿色分布均值位置在红蓝均值间的比例，即Kalman增益Kg。

根据数学上两正态分布相乘仍然是正态分布，由公式(3)得到Kg=0.5^2/(0.52+0.4^2)，所以Kg=0.61。（注意kg是方差的概念，不是均方差，网上很多文献kg用错，开了根号，得到0.78）我们可以估算出k时刻的实际位置是：23+0.61*(25-23)=24.22cm，见公式(1)。可以看出，因为雷达的方差比较小（比较相信雷达），所以估算出的最优位置值偏向雷达测量的值。

现在我们已经得到k时刻的最优位置值了，下一步就是要进入k+1时刻，进行新的最优估算。到现在为止，好像还没看到什么自回归的东西出现。对了，在进入k+1时刻之前，我们还要算出k时刻那个最优值（24.22cm）的偏差。算法如下：((1-Kg)*0.5²⁾0.5=0.312，见公式(2)。这里的0.5就是上面的k时刻你预测的那个23cm位置的均方差，得出的0.312cm就是进入k+1时刻以后k时刻估算出的最优位置值的均方差（对应于上面的0.3cm），于是我们可以把绿色分布当做第一张图中的红色分布对t=k+1时刻进行预测，算法就可以开始循环往复了。

说明一下，由于上面我们只对小车位移这个一维量（向量）做了估计，因此Kalman增益是标量。如果状态向量是多维，那么方差就该变为协方差，从而引入协方差矩阵的迭代，Kalman增益也变成了矩阵。需要采用公式(4)-(6)来求解Kalman增益矩阵和k时刻的最优值和协方差矩阵。无论是多少维的向量空间，上面描述给出了Kalman滤波算法的本质就是利用两个正态分布的融合仍是正态分布这一特性进行迭代而已。

4.卡尔曼滤波的严格数学描述

有了上述的理解，下面就要言归正传，讨论真正工程系统上的卡尔曼滤波。

首先，我们先要引入一个离散控制过程的系统。该系统可用一个线性随机微分方程（Linear Stochastic Difference equation）来描述：

X(k)=A X(k-1)+B U(k)+W(k)

再加上系统的测量值：

Z(k)=H X(k)+V(k)

上两式子中，X(k)是k时刻的系统状态，U(k)是k时刻对系统的控制量，A和B是系统参数，对于多模型系统，它们为矩阵。而Z(k)是k时刻的测量值，H是测量系统的参数，对于多测量系统，H为矩阵。W(k)和V(k)分别表示过程和测量的噪声。他们被假设成高斯白噪声(White Gaussian Noise)，他们的协方差(covariance)分别是Q，R（这里我们假设他们不随系统状态变化而变化）。

对于满足上面的条件(线性随机微分系统，过程和测量都是高斯白噪声)，卡尔曼滤波器是最优的信息处理器。下面我们结合他们的协方差来估算系统的最优化输出（类似上一节小车一维的例子，现在扩展到多维）。

首先我们要利用系统的过程模型，来预测下一状态的系统。假设现在的系统状态是k，根据系统的模型，可以基于系统的上一状态而预测出现在状态：

X(k|k-1)=A X(k-1|k-1)+B U(k) ………… (7)

式(7)中，X(k|k-1)是利用上一状态预测的结果，X(k-1|k-1)是上一状态最优的结果，U(k)为现在状态的控制量，如果没有控制量，它可以为0。

到现在为止，我们的系统结果已经更新了，可是，对应于X(k|k-1)的协方差还没更新。我们用P表示协方差(covariance)：

P(k|k-1)=A P(k-1|k-1) A’+Q ……… (8)

式(8)中，P(k|k-1)是X(k|k-1)对应的协方差，P(k-1|k-1)是X(k-1|k-1)对应的协方差，A’表示A的转置矩阵，Q是系统过程的协方差。式子7，8就是卡尔曼滤波器5个公式当中的前两个，也就是对系统的预测。

现在我们有了现在状态的预测结果，然后我们再收集现在状态的测量值。结合预测值和测量值，我们可以得到现在状态(k)的最优化估算值X(k|k)：

X(k|k)= X(k|k-1)+Kg(k) (Z(k)-H X(k|k-1))……… (9)

其中Kg为卡尔曼增益(Kalman Gain)：

Kg(k)= P(k|k-1) H’ / (H P(k|k-1) H’ + R)……… (10)

到现在为止，我们已经得到了k状态下最优的估算值X(k|k)。但是为了要令卡尔曼滤波器不断的运行下去直到系统过程结束，我们还要更新k状态下X(k|k)的协方差：

P(k|k)=（I-Kg(k) H）P(k|k-1) ………(11)

其中I为1的矩阵，对于单模型单测量，I=1。当系统进入k+1状态时，P(k|k)就是式子(8)的P(k-1|k-1)。这样，算法就可以自回归的运算下去。

5.卡尔曼滤波的编程实现

卡尔曼滤波器的原理基本描述了，式子8，9，10，11和12就是他的5个基本公式。根据这5个公式，可以很容易用计算机编程实现，具体思想如下：

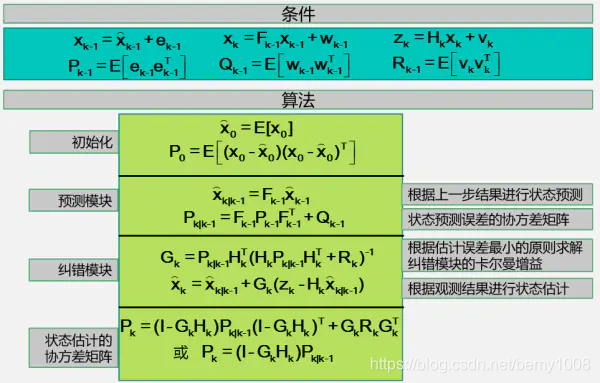
假设如下一个系统：

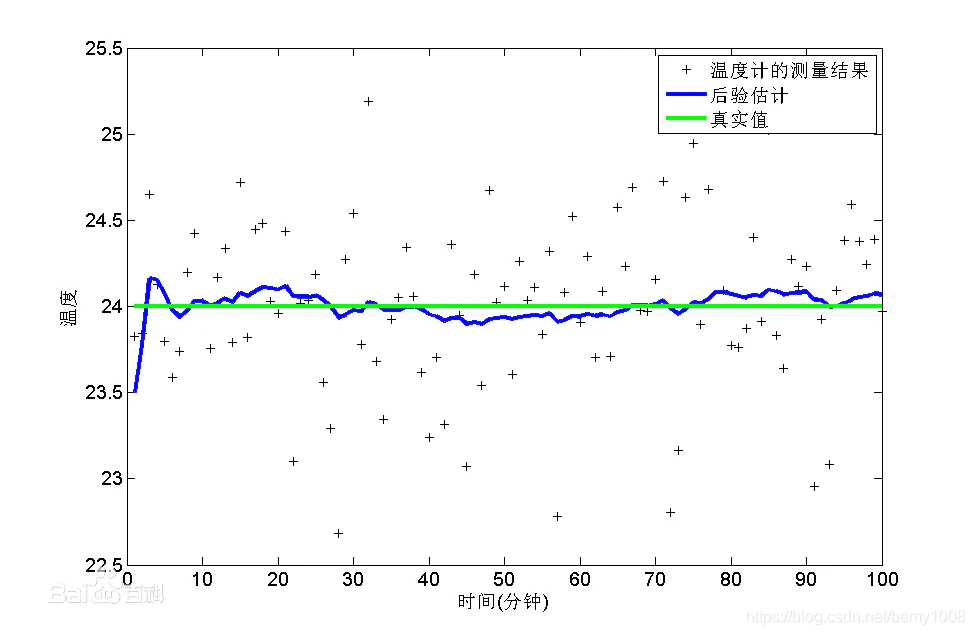
房间内连续两个时刻温度差值的标准差为0.02度，温度计的测量值误差的标准差为0.5度，房间温度的真实值为24度，对温度的初始估计值为23.5度，误差的方差为1。

MatLab仿真的代码如下：

% Kalman filter example of temperaturemeasurement in Matlab

% This M code is modified from Xuchen Yao’smatlab on 2013/4/18

%房间当前温度真实值为24度，认为下一时刻与当前时刻温度相同，误差为0.02度（即认为连续的两个时刻最多变化0.02度）。

%温度计的测量误差为0.5度。

%开始时，房间温度的估计为23.5度，误差为1度。

clear all;

close all;

% intial parameters

n_iter = 100; %计算连续n_iter个时刻

sz = [n_iter, 1]; % size of array. n_iter行，1列

x = 24; %温度的真实值

Q = 4e-4; %过程方差，反应连续两个时刻温度方差。更改查看效果

R = 0.25; %测量方差，反应温度计的测量精度。更改查看效果

z = x + sqrt®*randn(sz); % z是温度计的测量结果，在真实值的基础上加上了方差为0.25的高斯噪声。

%对数组进行初始化

xhat=zeros(sz); %对温度的后验估计。即在k时刻，结合温度计当前测量值与k-1时刻先验估计，得到的最终估计值

P=zeros(sz); %后验估计的方差

xhatminus=zeros(sz); %温度的先验估计。即在k-1时刻，对k时刻温度做出的估计

Pminus=zeros(sz); %先验估计的方差

K=zeros(sz); %卡尔曼增益，反应了温度计测量结果与过程模型（即当前时刻与下一时刻温度相同这一模型）的可信程度

% intial guesses

xhat(1) = 23.5; %温度初始估计值为23.5度

P(1) =1; %误差方差为1

for k = 2:n_iter

%时间更新（预测）

xhatminus(k) = xhat(k-1); %用上一时刻的最优估计值来作为对当前时刻的温度的预测

Pminus(k) = P(k-1)+Q; %预测的方差为上一时刻温度最优估计值的方差与过程方差之和

%测量更新（校正）

K(k) = Pminus(k)/( Pminus(k)+R ); %计算卡尔曼增益

xhat(k) =

xhatminus(k)+K(k)*(z(k)-xhatminus(k)); %结合当前时刻温度计的测量值，对上一时刻的预测进行校正，得到校正后的最优估计。该估计具有最小均方差

P(k) = (1-K(k))*Pminus(k); %计算最终估计值的方差

end

FontSize=14;

LineWidth=3;

figure();

plot(z,‘k+’); %画出温度计的测量值

hold on;

plot(xhat,‘b-’,‘LineWidth’,LineWidth) %画出最优估计值

hold on;

plot(x*ones(sz),‘g-’,‘LineWidth’,LineWidth);

%画出真实值

legend(‘温度计的测量结果’, ‘后验估计’, ‘真实值’);

xl=xlabel(‘时间(分钟)’);

yl=ylabel(‘温度’);

set(xl,‘fontsize’,FontSize);

set(yl,‘fontsize’,FontSize);

hold off;

set(gca,‘FontSize’,FontSize);

figure();

valid_iter = [2:n_iter]; % Pminus not validat step 1

plot(valid_iter,P([valid_iter]),‘LineWidth’,LineWidth);

%画出最优估计值的方差

legend(‘后验估计的误差估计’);

xl=xlabel(‘时间(分钟)’);

yl=ylabel(‘℃^2’);

set(xl,‘fontsize’,FontSize);

set(yl,‘fontsize’,FontSize);

set(gca,‘FontSize’,FontSize);

计算结果如图所示：

另外，跨平台计算机视觉库Opencv目标版本中带有kalman这个类，可以使用它来完成一些跟踪目的。下面来看看使用Kalman编程的主要步骤：

步骤一：

Kalman这个类需要初始化下面变量：

转移矩阵，测量矩阵，控制向量(没有的话，就是0)，过程噪声协方差矩阵，测量噪声协方差矩阵，后验错误协方差矩阵，前一状态校正后的值，当前观察值。

步骤二：

调用kalman这个类的predict方法得到状态的预测值矩阵，预测状态的计算公式如下：

predicted state (x’(k)):x’(k)=Ax(k-1)+Bu(k)

其中x(k-1)为前一状态的校正值，第一个循环中在初始化过程中已经给定了，后面的循环中Kalman这个类内部会计算。A,B,u(k),也都是给定了的值。这样进过计算就得到了系统状态的预测值x’(k)了。

步骤三：

调用kalman这个类的correct方法得到加入观察值校正后的状态变量值矩阵，其公式为：

corrected state (x(k)):x(k)=x’(k)+K(k)(z(k)-Hx’(k))

其中x’(k)为步骤二算出的结果，z(k)为当前测量值，是我们外部测量后输入的向量。H为Kalman类初始化给定的测量矩阵。K(k)为Kalman增益，其计算公式为：

Kalman gain matrix (K(k)): K(k)=P’(k)Htinv(H*P’(k)*Ht+R)

计算该增益所依赖的变量要么初始化中给定，要么在kalman理论中通过其它公式可以计算。

经过步骤三后，我们又重新获得了这一时刻的校正值，后面就不断循环步骤二和步骤三即可完成Kalman滤波过程。