论文地址:https://www.jmlr.org/papers/volume23/19-497/19-497.pdf
相关博客:
【自然语言处理】【聚类】基于神经网络的聚类算法DEC
【自然语言处理】【聚类】基于对比学习的聚类算法SCCL
【自然语言处理】【聚类】DCSC:利用基于对比学习的半监督聚类算法进行意图挖掘
【自然语言处理】【聚类】DeepAligned:使用深度对齐聚类发现新意图
【自然语言处理】【聚类】CDAC+:通过深度自适应聚类发现新意图
【计算机视觉】【聚类】DeepCluster:用于视觉特征无监督学习的深度聚类算法
【计算机视觉】【聚类】SwAV:基于对比簇分配的无监督视觉特征学习
【计算机视觉】【聚类】CC:对比聚类
【计算机视觉】【聚类】SeLa:同时进行聚类和表示学习的自标注算法
【自然语言处理】【聚类】ECIC:通过迭代分类增强短文本聚类
【自然语言处理】【聚类】TELL:可解释神经聚类
一、简介
本文研究了可解释AI( XAI \text{XAI} XAI)和数据聚类这两个挑战性问题。第一个问题是如何设计一种具有固定可解释性的神经网络,而不是给出一个黑盒模型的事后解释。第二个问题是,使用可微分神经网络来实现离散的 k-means \text{k-means} k-means,其拥有具有并行计算、在线聚类和聚类友好的表示学习等优势。为了解决这两个挑战,本文设计了一种新颖的神经网络,该网络是普通 k-means \text{k-means} k-means的可微分版本,称为 TELL(Terpretable nEuraL cLustering) \text{TELL(Terpretable nEuraL cLustering)} TELL(Terpretable nEuraL cLustering)。本文贡献有三部分:首先,许多可解释工作专注在有监督范式,本文的工作是少有的无监督学习上的可解释性研究。其次, TELL \text{TELL} TELL是一个可解释,或者称为本质上可解释且透明的模型。相反,许多现有的可解释AI研究( XAI \text{XAI} XAI)采用各种方式理解带有事后解释的黑盒模型。最后, TELL \text{TELL} TELL具有 k-means \text{k-means} k-means所期望的各种性质,包括但不限于在线聚类、即插即用、并行计算和可证明的收敛。
二、标准 k-means \text{k-means} k-means的不足
给定一个数据集
X
=
{
X
1
,
X
2
,
…
,
X
n
}
\textbf{X}=\{\textbf{X}_1,\textbf{X}_2,\dots,\textbf{X}_n\}
X={X1,X2,…,Xn},
k-means
\text{k-means}
k-means的目标是通过最小化簇内数据点的距离来将每个数据点
X
i
\textbf{X}_i
Xi分组至
k
≤
n
k\leq n
k≤n个集合
S
=
{
S
1
,
S
2
,
…
,
S
n
}
\mathcal{S}=\{\mathcal{S}_1,\mathcal{S}_2,\dots,\mathcal{S}_n\}
S={S1,S2,…,Sn}的一个,即
argmin
S
∑
j
∑
X
i
∈
S
j
∥
X
i
−
Ω
j
∥
2
2
(1)
\mathop{\text{argmin}}_\mathcal{S}\sum_j\sum_{\textbf{X}_i\in\mathcal{S}_j}\parallel\textbf{X}_i-\Omega_j\parallel_2^2 \tag{1}
argminSj∑Xi∈Sj∑∥Xi−Ωj∥22(1)
其中,
Ω
j
\Omega_j
Ωj表示第
j
j
j个簇中心,其是由
S
j
\mathcal{S}_j
Sj中数据点的均值计算所得。即
Ω
j
=
1
∣
S
j
∣
∑
X
i
∈
S
j
X
i
(2)
\Omega_j=\frac{1}{|\mathcal{S}_j|}\sum_{\textbf{X}_i\in\mathcal{S}_j}\textbf{X}_i\tag{2}
Ωj=∣Sj∣1Xi∈Sj∑Xi(2)
其中,
∣
S
j
∣
|\mathcal{S}_j|
∣Sj∣表示第
j
j
j个簇中数据点的个数。
为了求解等式 ( 1 ) (1) (1),采用 EM \text{EM} EM方式来迭代更新 S \mathcal{S} S和 Ω \Omega Ω,即固定一个来优化另一个。这样的迭代优化有几个缺点:
首先,在欧式空间中寻找 k-means \text{k-means} k-means的最优解是NP难问题,即使对于两个簇的聚类。为了缓解NP难问题,一些 k-means \text{k-means} k-means的变体被提出,例如参数方法 Fuzzy c-means \text{Fuzzy c-means} Fuzzy c-means。然而,这些方法对超参数非常敏感且非常难以调优。
其次,标准 k-means \text{k-means} k-means在每次迭代中都需要在整个数据集上计算簇中心。当数据以流式呈现时,那么在大规模数据和在线聚类场景中都无法使用。更准确地说,虽然能够将新数据分配至最近的簇,但无法进一步更新簇中心,除非在所有数据上再重新跑整个算法。
最后,标准 k-means \text{k-means} k-means在固定的输入上执行,并不能辅助表示学习。深度学习的成功,很大程度上依赖端到端的学习,一个即插即用的神经聚类模块非常值得期待。在提出的方法 TELL \text{TELL} TELL中,聚类层能够仅执行聚类,也可以帮助网络以端到端的方式学习有益于聚类的表示。
三、聚类算法 TELL \text{TELL} TELL
1. k-means \text{k-means} k-means的神经网络实现
为了克服标准
k-means
\text{k-means}
k-means的缺点,通过重写等式
(1)
\text{(1)}
(1)将目标函数重写为神经层
min
∑
i
=
1
n
∑
j
=
1
k
I
j
(
X
i
)
∥
X
i
−
Ω
j
∥
2
2
(3)
\text{min}\sum_{i=1}^n\sum_{j=1}^k\mathcal{I}_j(\textbf{X}_i)\parallel\textbf{X}_i-\Omega_j\parallel_2^2 \tag{3}
mini=1∑nj=1∑kIj(Xi)∥Xi−Ωj∥22(3)
其中,
I
j
\mathcal{I}_j
Ij表示样本
X
i
\textbf{X}_i
Xi是否属于簇
Ω
j
\Omega_j
Ωj。
等式
(
3
)
(3)
(3)的右半部分可以被扩展为
∥
X
i
−
Ω
j
∥
2
2
=
∥
X
i
∥
2
2
−
2
Ω
j
⊤
X
i
+
∥
Ω
j
∥
2
2
(4)
\parallel\textbf{X}_i-\Omega_j\parallel_2^2=\parallel\textbf{X}_i\parallel_2^2-2\Omega_j^\top\textbf{X}_i+\parallel\Omega_j\parallel_2^2\tag{4}
∥Xi−Ωj∥22=∥Xi∥22−2Ωj⊤Xi+∥Ωj∥22(4)
然后定义
W
j
=
2
Ω
j
,
b
j
=
−
∥
Ω
j
∥
2
2
,
∥
X
i
∥
2
2
=
β
i
≥
0
(5)
\textbf{W}_j=2\Omega_j,\quad\textbf{b}_j=-\parallel\Omega_j\parallel_2^2,\quad\parallel\textbf{X}_i\parallel_2^2=\beta_i\geq0\tag{5}
Wj=2Ωj,bj=−∥Ωj∥22,∥Xi∥22=βi≥0(5)
其中,
W
j
\textbf{W}_j
Wj是矩阵
W
\textbf{W}
W的第
j
j
j列,
b
j
\textbf{b}_j
bj表示向量
b
\textbf{b}
b的第
j
j
j个分量,
β
i
\beta_i
βi是一个对应于数据点
X
i
\textbf{X}_i
Xi长度的非负常数。
根据上面的公式,可以等价地将数据点
X
i
\textbf{X}_i
Xi和簇中心
Ω
j
\Omega_j
Ωj的距离重写为
∥
X
i
−
Ω
j
∥
2
2
=
β
i
−
W
j
⊤
X
i
−
b
j
(6)
\parallel\textbf{X}_i-\Omega_j\parallel_2^2=\beta_i-\textbf{W}_j^\top\textbf{X}_i-\textbf{b}_j\tag{6}
∥Xi−Ωj∥22=βi−Wj⊤Xi−bj(6)
对于给定的temperature参数
τ
\tau
τ,放松类别变量
I
j
(
X
i
)
\mathcal{I}_j(\textbf{X}_i)
Ij(Xi)为
I
j
(
X
i
)
=
exp
(
−
∥
X
i
−
Ω
j
∥
2
2
/
τ
)
∑
k
exp
(
−
∥
X
i
−
Ω
k
∥
2
2
/
τ
)
)
(7)
\mathcal{I}_j(\textbf{X}_i)=\frac{\text{exp}(-\parallel\textbf{X}_i-\Omega_j\parallel_2^2/\tau)}{\sum_k\text{exp}(-\parallel\textbf{X}_i-\Omega_k\parallel_2^2/\tau))} \tag{7}
Ij(Xi)=∑kexp(−∥Xi−Ωk∥22/τ))exp(−∥Xi−Ωj∥22/τ)(7)
事实上,上面关于
I
j
(
X
i
)
\mathcal{I}_j(\textbf{X}_i)
Ij(Xi)的定义将其看作
X
i
\textbf{X}_i
Xi在第
j
j
j个簇的注意力。
合并等式
(
6
)
(6)
(6)和等式
(
7
)
(7)
(7),
I
j
(
X
i
)
\mathcal{I}_j(\textbf{X}_i)
Ij(Xi)能够被提出的神经层来计算
I
j
(
X
i
)
=
exp
(
(
W
j
⊤
X
i
+
b
j
−
β
i
)
/
τ
)
∑
k
exp
(
(
W
k
⊤
X
i
+
b
k
−
β
i
)
/
τ
)
(8)
\mathcal{I}_j(\textbf{X}_i)=\frac{\text{exp}((\textbf{W}_j^\top\textbf{X}_i+\textbf{b}_j-\beta_i)/\tau)}{\sum_k\text{exp}((\textbf{W}_k^\top\textbf{X}_i+\textbf{b}_k-\beta_i)/\tau)}\tag{8}
Ij(Xi)=∑kexp((Wk⊤Xi+bk−βi)/τ)exp((Wj⊤Xi+bj−βi)/τ)(8)
连续类别变量
I
j
(
X
i
)
\mathcal{I}_j(\textbf{X}_i)
Ij(Xi)可以使用任何规范化函数来计算,包括但不限于
softmax
\text{softmax}
softmax。为了避免对temperature参数进行大量的调整,本文实现时采用了替代方案,通过简单地保留
I
j
(
X
i
)
\mathcal{I}_j(\textbf{X}_i)
Ij(Xi)的最大分量。当
τ
\tau
τ趋于0时,其与标准
k-means
\text{k-means}
k-means保持一致。
2. 解耦网络权重和偏差
为了避免复杂数学符号带来的混淆,不失一般性地,在下面的分析中仅考虑一个样本
x
\textbf{x}
x的例子。在这个例子中,
TELL
\text{TELL}
TELL的目标函数能够被形式化为
L
=
∑
j
L
j
=
∑
j
I
j
(
−
W
j
⊤
x
−
b
j
+
β
)
(9)
\mathcal{L}=\sum_j\mathcal{L}_j=\sum_j\mathcal{I}_j(-\textbf{W}_j^\top\textbf{x}-\textbf{b}_j+\beta)\tag{9}
L=j∑Lj=j∑Ij(−Wj⊤x−bj+β)(9)
其中,
I
j
\mathcal{I}_j
Ij是
I
j
(
x
)
\mathcal{I}_j(\textbf{x})
Ij(x)的简写。
虽然根据等式 ( 5 ) (5) (5)的定义来看 W \textbf{W} W和 b \textbf{b} b是天然耦合的,即 b j = − ∥ W j ∥ 2 2 4 \textbf{b}_j=-\frac{\parallel\textbf{W}_j\parallel_2^2}{4} bj=−4∥Wj∥22,但是作者从理论上证明了训练过程中 W \textbf{W} W和 b \textbf{b} b是应该被解耦的。换句话说, W \textbf{W} W和 b \textbf{b} b应该被独立优化并且最终的簇中心 Ω ∗ \Omega^* Ω∗通过 Ω ∗ = 1 2 W ∗ \Omega^*=\frac{1}{2}\textbf{W}^* Ω∗=21W∗来获得。
证明解耦
W
\textbf{W}
W和
b
\textbf{b}
b的必要性,需要将等式
(
9
)
(9)
(9)重写为
L
=
−
∑
j
exp
(
(
b
j
+
W
j
⊤
x
−
β
)
/
τ
)
(
b
j
+
W
j
⊤
x
−
β
)
∑
k
exp
(
(
b
k
+
W
k
⊤
x
−
β
)
/
τ
)
=
−
∑
j
exp
(
z
j
/
τ
)
∑
k
exp
(
z
k
/
τ
)
z
j
=
−
∑
j
f
(
z
j
)
(10)
\begin{aligned} \mathcal{L}&=-\sum_j\frac{\text{exp}((\textbf{b}_j+\textbf{W}_j^\top\textbf{x}-\beta)/\tau)(\textbf{b}_j+\textbf{W}_j^\top\textbf{x}-\beta)}{\sum_k\text{exp}((\textbf{b}_k+\textbf{W}_k^\top\textbf{x}-\beta)/\tau)} \\ &=-\sum_j\frac{\text{exp}(\textbf{z}_j/\tau)}{\sum_k\text{exp}(\textbf{z}_k/\tau)}\textbf{z}_j\\ &=-\sum_j f(\textbf{z}_j) \end{aligned}\tag{10}
L=−j∑∑kexp((bk+Wk⊤x−β)/τ)exp((bj+Wj⊤x−β)/τ)(bj+Wj⊤x−β)=−j∑∑kexp(zk/τ)exp(zj/τ)zj=−j∑f(zj)(10)
其中,
z
j
=
(
−
∥
W
j
∥
2
2
4
+
W
j
⊤
x
−
β
)
\textbf{z}_j=(-\frac{\parallel\textbf{W}_j\parallel_2^2}{4}+\textbf{W}_j^\top\textbf{x}-\beta)
zj=(−4∥Wj∥22+Wj⊤x−β)。
相应地,目标损失函数变为
max
∑
j
f
(
z
j
)
s.t.
z
j
=
−
∥
W
j
∥
2
2
4
+
W
j
⊤
x
−
β
(11)
\text{max}\;\sum_j f(\textbf{z}_j) \\ \text{s.t.}\quad\textbf{z}_j=-\frac{\parallel\textbf{W}_j\parallel_2^2}{4}+\textbf{W}_j^\top\textbf{x}-\beta \tag{11}
maxj∑f(zj)s.t.zj=−4∥Wj∥22+Wj⊤x−β(11)
可以看到,等式当
W
\textbf{W}
W和
b
\textbf{b}
b耦合时,即
b
j
=
−
∥
W
j
∥
2
2
4
\textbf{b}_j=-\frac{\parallel\textbf{W}_j\parallel_2^2}{4}
bj=−4∥Wj∥22,等式
(
11
)
(11)
(11)等价于等式
(
3
)
(3)
(3)。当
z
=
∞
\textbf{z}=\infty
z=∞时,等式
(
11
)
(11)
(11)在边界
z
1
=
z
2
=
…
\textbf{z}_1=\textbf{z}_2=\dots
z1=z2=…获得最优值
f
(
z
)
=
∞
f(\textbf{z})=\infty
f(z)=∞。存在一个
z
∗
\textbf{z}^*
z∗使
z
j
=
z
∗
\textbf{z}_j=\textbf{z}^*
zj=z∗且
f
(
z
∗
)
f(\textbf{z}^*)
f(z∗)达到最优值。我们总能找到
W
j
\textbf{W}_j
Wj和
b
j
\textbf{b}_j
bj使得
b
j
+
W
j
⊤
x
−
β
=
z
∗
\textbf{b}_j+\textbf{W}_j^\top\textbf{x}-\beta=\textbf{z}^*
bj+Wj⊤x−β=z∗,而不必保证
W
j
\textbf{W}_j
Wj和
b
j
\textbf{b}_j
bj满足
−
∥
W
j
∥
2
2
4
+
W
j
⊤
x
−
β
=
z
∗
-\frac{\parallel\textbf{W}_j\parallel_2^2}{4}+\textbf{W}_j^\top\textbf{x}-\beta=\textbf{z}^*
−4∥Wj∥22+Wj⊤x−β=z∗。虽然上面的分析是基于单个样本的,结论仍然适用于多个样本,因为它们彼此独立。从某种意义上,我们必须在训练中解耦
W
j
\textbf{W}_j
Wj和
b
j
\textbf{b}_j
bj来避免平凡解。
3. 规范化聚类层的权重和梯度

上一小节,我们展示了解耦 W \textbf{W} W和 b \textbf{b} b来阻止网络退化为平凡解的必要性。然而,我们进一步发现解耦 W \textbf{W} W和 b \textbf{b} b并直接优化它们将导致发散和训练不稳定。为了解决这个问题,我们提出规范化聚类层的权重和它的梯度来实现稳定训练,如上图所示。
具体来说,当
W
\textbf{W}
W和
b
\textbf{b}
b被解耦时,最小化等式
(
9
)
(9)
(9)的损失函数
∑
j
I
j
(
−
W
j
⊤
x
−
b
j
+
β
)
\sum_j\mathcal{I}_j(-\textbf{W}_j^\top\textbf{x}-\textbf{b}_j+\beta)
∑jIj(−Wj⊤x−bj+β)将导致
W
j
⊤
\textbf{W}_j^\top
Wj⊤和
b
j
\textbf{b}_j
bj为正无穷,如上图(a)所示。在这个例子中,聚类层的优化永远都不会收敛。为了解决这个问题,作者提出了同时规范化聚类层的权重和偏差。实际上,作者采用了更直接的方法来簇中心
Ω
j
,
j
∈
[
1
,
k
]
\Omega_j,j\in[1,k]
Ωj,j∈[1,k]规范化长度为1,即
Ω
j
=
Ω
j
/
∥
Ω
j
∥
\Omega_j=\Omega_j/\parallel\Omega_j\parallel
Ωj=Ωj/∥Ωj∥。因此,为了保持欧式距离的有效性,数据点也被规范化为具有单位长度,即
β
=
1
\beta=1
β=1。从这个意义上来说,
W
j
\textbf{W}_j
Wj的长度为2且
b
j
\textbf{b}_j
bj是个常数。因此,等式
(
9
)
(9)
(9)的损失函数可以重写为
L
=
∑
j
L
j
=
∑
j
I
j
(
2
−
W
j
⊤
x
)
(12)
\mathcal{L}=\sum_j\mathcal{L}_j=\sum_j\mathcal{I}_j(2-\textbf{W}_j^\top\textbf{x}) \tag{12}
L=j∑Lj=j∑Ij(2−Wj⊤x)(12)
在实践中,使用
SGD
\text{SGD}
SGD来优化
W
j
\textbf{W}_j
Wj,在每次更新后都需要重新对其进行规范化。然而,如上图(b)所示,当梯度远大于
W
j
\textbf{W}_j
Wj的长度,在每次更新后
W
j
\textbf{W}_j
Wj的变化会特别大。使用
MNIST
\text{MNIST}
MNIST数据集作为例子,一开始
W
o
l
d
\textbf{W}_{old}
Wold可能对应数字"3"的簇中心。然而,当梯度太大时,经过优化后
W
n
e
w
\textbf{W}_{new}
Wnew可能迁移至数字"5"。换句话说,在每次迭代中
W
j
\textbf{W}_j
Wj的内在语义信息都可能不同,这将导致不稳定的优化并且导致网络很难收敛。
考虑到前面提到的缺点,作者提出了同时上图©中同时规范化权重和梯度。当梯度足够小时,簇中心被适度优化并且其语义信息在整个训练过程中都保持一致,也就意味着稳定的训练。实践中,规范化梯度为 W j \textbf{W}_j Wj长度的10%。
4. 用于聚类和表示学习的端到端训练

基于上面的讨论,通过在神经层上使用下面的可微分损失函数来迁移标准的
k-means
\text{k-means}
k-means。
L
=
∑
i
,
j
I
j
(
X
i
)
(
2
−
W
j
⊤
X
i
)
(13)
\mathcal{L}=\sum_{i,j}\mathcal{I}_j(\textbf{X}_i)(2-\textbf{W}_j^\top\textbf{X}_i)\tag{13}
L=i,j∑Ij(Xi)(2−Wj⊤Xi)(13)
相比于标准
k-means
\text{k-means}
k-means,
TELL
\text{TELL}
TELL的主要优势是即插即用,即能够插入仍然神经网络里利用深度表示改善聚类。为了这个目的,不直接在原始特征上执行聚类,而是使用最小化重构误差的自编码器来抽取判别性特征
h
=
{
h
1
,
h
2
,
…
}
\textbf{h}=\{\textbf{h}_1,\textbf{h}_2,\dots\}
h={h1,h2,…}。
h
i
=
f
(
X
i
)
X
^
i
=
g
(
h
i
)
L
r
e
c
=
∑
i
∥
X
i
−
X
^
i
∥
2
2
(14)
\textbf{h}_i=f(\textbf{X}_i) \\ \hat{\textbf{X}}_i= g(\textbf{h}_i) \\ \mathcal{L}_{rec}=\sum_{i}\parallel\textbf{X}_i-\hat{\textbf{X}}_i\parallel_2^2 \tag{14}
hi=f(Xi)X^i=g(hi)Lrec=i∑∥Xi−X^i∥22(14)
其中,
f
(
⋅
)
f(\cdot)
f(⋅)和
g
(
⋅
)
g(\cdot)
g(⋅)表示编码器和解码器,
h
i
\textbf{h}_i
hi被规范化为单位长度。在等式
(
13
)
(13)
(13)中使用
h
i
\textbf{h}_i
hi替换
X
i
\textbf{X}_i
Xi,
TELL
\text{TELL}
TELL的整体损失合并了重构损失和聚类损失
L
=
L
r
e
c
+
λ
L
c
l
u
=
∑
i
∥
X
i
−
g
(
f
(
X
i
)
)
∥
2
2
+
λ
∑
i
,
j
I
j
(
X
i
)
(
2
−
W
j
⊤
f
(
X
i
)
)
(15)
\begin{aligned} \mathcal{L}&=\mathcal{L}_{rec}+\lambda\mathcal{L}_{clu} \\ &=\sum_i\parallel\textbf{X}_i-g(f(\textbf{X}_i))\parallel_2^2+\lambda\sum_{i,j}\mathcal{I}_j(\textbf{X}_i)(2-\textbf{W}_j^\top f(\textbf{X}_i)) \end{aligned} \tag{15}
L=Lrec+λLclu=i∑∥Xi−g(f(Xi))∥22+λi,j∑Ij(Xi)(2−Wj⊤f(Xi))(15)
其中,
λ
=
0.01
\lambda=0.01
λ=0.01。
可以看出,重构损失函数被用于同时优化编码器 f ( ⋅ ) f(\cdot) f(⋅)和解码器 g ( ⋅ ) g(\cdot) g(⋅)。对于聚类损失函数,已经证明其可以优化聚类层权重 W j \textbf{W}_j Wj。这里,为了进一步改善特征的表达能力,也使用聚类损失函数优化编码器 f ( ⋅ ) f(\cdot) f(⋅)来特征拉近至对应的簇中心。实践中,为了稳定的训练,等式 ( 15 ) (15) (15)右侧被用于交替优化 W \textbf{W} W和 f ( ⋅ ) f(\cdot) f(⋅)。整体的端到端训练框架图如上图所示。
四、 TELL \text{TELL} TELL的解释性

虽然近些年可解释性AI( XAI \text{XAI} XAI)实现了显著的进步,但是文献中对于" explainability \text{explainability} explainability“和” interpretability \text{interpretability} interpretability"的误用是达成共识的一个障碍。简单来说, explainability \text{explainability} explainability是指通过各种方法进行事后归因解释来增强对模型的理解,例如: text explanations \text{text explanations} text explanations、 visual explanations \text{visual explanations} visual explanations、 explanations by simplification \text{explanations by simplification} explanations by simplification和 feature relevance explanations \text{feature relevance explanations} feature relevance explanations技术。不同于 explanations \text{explanations} explanations, interpretability \text{interpretability} interpretability植根于模型本身的设计,其非常值得期待但十分有挑战。 interpretability \text{interpretability} interpretability也表达透明性,其表示模型的可分解性和算法的透明性。下面将展示 TELL \text{TELL} TELL具有两种可解释特征。
TELL \text{TELL} TELL用于模型可分解性,其意味着解释聚类层的每个部分是可行的。换句话说,聚类层的输入、权重参数、激活函数和损失函数都是可解释的。具体来说,聚类层的输入对应给定的数据点,权重矩阵 W \textbf{W} W是簇中心 Ω \Omega Ω, argmax \text{argmax} argmax激活函数被用于实现数据点至最近簇的分配,损失函数则是从标准 k-means \text{k-means} k-means推导出,如等式 ( 4-5 ) (\text{4-5}) (4-5)。为了加强可解释性的主张,作者还通过可视化从 Ω \Omega Ω重构的簇中心来作事后解释。如上图所示,重构的簇中心与 MNIST \text{MNIST} MNIST的数字完全对应,说明 TELL \text{TELL} TELL确实捕获到了内在的语义。
TELL \text{TELL} TELL也具有算法透明性,因为其动态行为可以从数学上进行推理,从而允许用户理解模型的行为。具体来说,作者不仅在理论上提供了收敛分析,而且展示了解耦 W \textbf{W} W和 b \textbf{b} b的必要性,以及规范化权重 W \textbf{W} W和梯度能够实现合适且稳定的优化。

此外,作者还从自然语言理解中流行的注意力机制来理解 TELL \text{TELL} TELL的工作方式。如上图所示, TELL \text{TELL} TELL的目标是学习一个划分簇中心的线性超平面 W \textbf{W} W。这个超平面能基于注意力将相似数据划分至相同的簇,并将不相似的数据划分至不同的簇。更具体的来说,通过等式 ( 6 ) (6) (6)学习超平面, TELL \text{TELL} TELL通过 ( 2 − W ⊤ X i ) (2-\textbf{W}^\top\textbf{X}_i) (2−W⊤Xi)计算输入 X i \textbf{X}_i Xi和簇中心 Ω \Omega Ω的不相似度。然后, TELL \text{TELL} TELL是基于 I ( X i ) \mathcal{I}(\textbf{X}_i) I(Xi)的加权不相似度之和。直觉上,这个注意力机制的实现如上图所示,其决定了 X i \textbf{X}_i Xi应该关注哪个簇中心。实际上,这里的注意力是簇分配。
五、收敛证明
在本小节,作者从理论上证明提出的损失函数 L \mathcal{L} L基于 SGD \text{SGD} SGD能够充分收敛。
为了便于展示,令
L
∗
\mathcal{L}^*
L∗表示最优损失函数,
L
t
∗
\mathcal{L}_t^*
Lt∗表示在步骤
t
t
t是的最小损失函数,
W
∗
\textbf{W}^*
W∗则是对应于最优簇中心
Ω
∗
\Omega^*
Ω∗的权重。这里考虑使用标准
SGD
\text{SGD}
SGD来优化网络
W
t
+
1
=
W
t
−
η
t
∇
L
(
W
t
)
(16)
\textbf{W}_{t+1}=\textbf{W}_t-\eta_t\nabla\mathcal{L}(\textbf{W}_t) \tag{16}
Wt+1=Wt−ηt∇L(Wt)(16)
其中,
∇
L
(
W
t
)
\nabla\mathcal{L}(\textbf{W}_t)
∇L(Wt)表示
L
\mathcal{L}
L关于
W
t
\textbf{W}_t
Wt的梯度。下面,将
∇
L
(
W
t
)
\nabla\mathcal{L}(\textbf{W}_t)
∇L(Wt)缩写为
∇
L
t
\nabla\mathcal{L}_t
∇Lt。
-
定义1: Lipschitz \text{Lipschitz} Lipschitz连续性
如果存在一个常数 ϵ > 0 \epsilon>0 ϵ>0,对于所有的 x 1 , x 2 ∈ Ω x_1,x_2\in\Omega x1,x2∈Ω都有
∥ f ( x 1 ) − f ( x 2 ) ∥ ≤ ϵ ∥ x 1 − x 2 ∥ (17) \parallel f(x_1)-f(x_2) \parallel\leq\epsilon\parallel x_1-x_2 \parallel \tag{17} ∥f(x1)−f(x2)∥≤ϵ∥x1−x2∥(17)则称函数 f ( x ) f(x) f(x)在集合 Ω \Omega Ω上是 Lipschitz \text{Lipschitz} Lipschitz连续的,其中 ϵ \epsilon ϵ被称为 Lipschitz \text{Lipschitz} Lipschitz常数。
TELL \text{TELL} TELL的损失函数 L \mathcal{L} L是 Lipschitz \text{Lipschitz} Lipschitz连续的, i.i.f. ∥ ∇ L t ∥ ≤ ϵ \text{i.i.f. }\parallel\nabla\mathcal{L}_t\parallel\leq \epsilon i.i.f. ∥∇Lt∥≤ϵ。换句话说,为了满足 Lipschitz \text{Lipschitz} Lipschitz连续性,需要证明 ∇ L t / τ \nabla\mathcal{L}_t/\tau ∇Lt/τ的上界是存在的。
-
定理1:存在 ϵ > 0 \epsilon>0 ϵ>0使得 ∥ ∇ L t ∥ ≤ ϵ \parallel\nabla\mathcal{L}_t\parallel\leq\epsilon ∥∇Lt∥≤ϵ,其中 ϵ = τ + 2 τ max ( ∥ z i ∥ ) \epsilon=\tau+2\tau\text{max}(\parallel\textbf{z}_i\parallel) ϵ=τ+2τmax(∥zi∥)和 z i = W i ⊤ x / τ \textbf{z}_i=\textbf{W}_i^\top\textbf{x}/\tau zi=Wi⊤x/τ。
定理1表明,当 ∥ z i ∥ \parallel\textbf{z}_i\parallel ∥zi∥是有界的,提出的损失函数 L ( W ) \mathcal{L}(\textbf{W}) L(W)将会有一个正实数 ϵ \epsilon ϵ的上界。事实上,对于任何真实世界中的数据集都存在 ∥ z i ∥ \parallel\textbf{z}_i\parallel ∥zi∥的上界。此外,不失一般性地,由于可以规范化 x \textbf{x} x和 Ω i \Omega_i Ωi来满足 ∥ x ∥ = ∥ Ω i ∥ = 1 \parallel\textbf{x}\parallel=\parallel\Omega_i\parallel=1 ∥x∥=∥Ωi∥=1,这样 ∥ W i ∥ = 2 \parallel\textbf{W}_i\parallel=2 ∥Wi∥=2就是边界。基于定理1,会有下面的定理2。
-
定理2:经过 T T T步骤后,总是能够发现足够解决最优值 L ∗ \mathcal{L}^* L∗的最优模型 L T ∗ \mathcal{L}_T^* LT∗,即
L T ∗ − L ∗ ≤ ∥ W 1 − W ∗ ∥ F 2 + ϵ 2 ∑ t T η t 2 2 ∑ t = 1 T η t (18) \mathcal{L}_T^*-\mathcal{L}^*\leq\frac{\parallel\textbf{W}_1-\textbf{W}^*\parallel_F^2+\epsilon^2\sum_t^T\eta_t^2}{2\sum_{t=1}^T\eta_t} \tag{18} LT∗−L∗≤2∑t=1Tηt∥W1−W∗∥F2+ϵ2∑tTηt2(18)
基于定理2可以推导出下面的两个引理。 -
引理1:对于固定大小的step(即 η t = η \eta_t=\eta ηt=η)且 T → ∞ T\rightarrow\infty T→∞,有
L T ∗ − L ∗ → η ϵ 2 2 (19) \mathcal{L}_T^*-\mathcal{L}^*\rightarrow\frac{\eta\epsilon^2}{2}\tag{19} LT∗−L∗→2ηϵ2(19) -
引理2:对于固定的step长度(即 η t = η / ∇ L t \eta_t=\eta/\nabla\mathcal{L}_t ηt=η/∇Lt)且 T → ∞ T\rightarrow\infty T→∞,有
L T ∗ − L ∗ → η ϵ 2 (19) \mathcal{L}_T^*-\mathcal{L}^*\rightarrow\frac{\eta\epsilon}{2}\tag{19} LT∗−L∗→2ηϵ(19)
六、实验


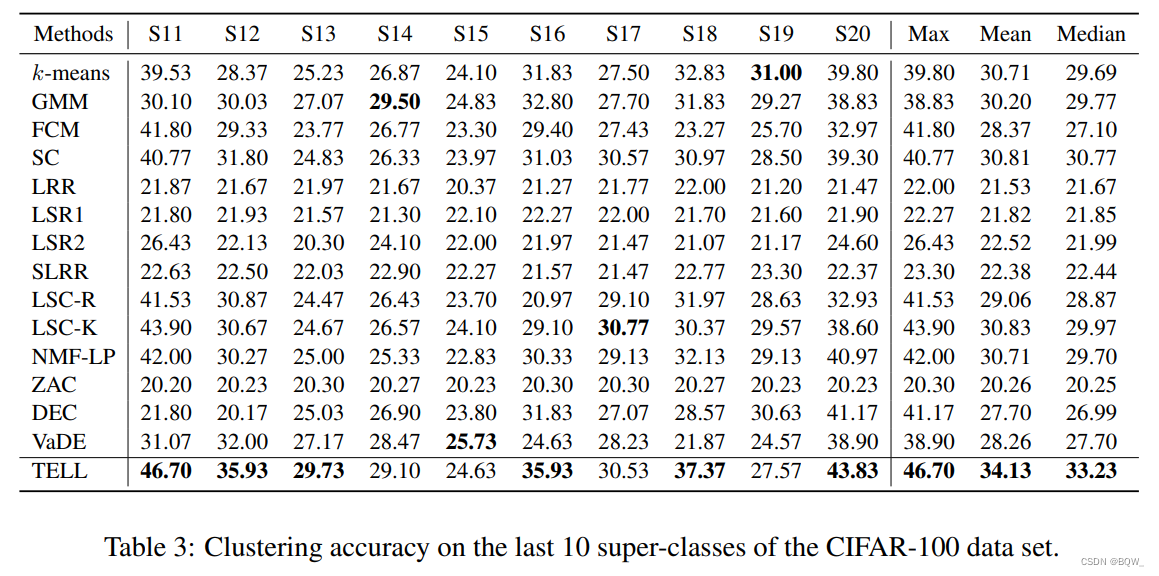








 本文介绍了一种名为TELL的神经网络聚类算法,它在无监督学习中实现可解释性,通过可微分的k-means改进,支持在线聚类和表示学习。文章详细阐述了算法原理、挑战及解决方案,包括解耦权重和偏差、规范化训练以及端到端的聚类与表示学习。
本文介绍了一种名为TELL的神经网络聚类算法,它在无监督学习中实现可解释性,通过可微分的k-means改进,支持在线聚类和表示学习。文章详细阐述了算法原理、挑战及解决方案,包括解耦权重和偏差、规范化训练以及端到端的聚类与表示学习。

















 241
241

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










