图马尔可夫网络：融合统计关系学习与图神经网络

©PaperWeekly 原创 · 作者｜石壮威

学校｜南开大学硕士

研究方向｜机器学习、图神经网络

论文标题：

GMNN: Graph Markov Neural Networks

收录会议：

ICML 2019

论文地址：

https://arxiv.org/abs/1905.06214

代码地址：

https://github.com/DeepGraphLearning/GMNN

 

本文 [1] 研究了图上的半监督节点分类问题。在此前的文献中，基于统计关系学习（例如马尔科夫随机场）和图神经网络（例如图卷积网络）的方法都已被广泛应用于这类问题。统计关系学习方法通过对象标签的依赖关系建模条件随机场，而图神经网络则以端到端训练的形式，提升了图学习的效率。

在本文中，作者提出图马尔可夫神经网络（Graph Markov Neural Networks ，GMNN）。GMNN 以条件随机场建模对象标签的联合分布，用变分 EM 算法进行有效训练。在 E-step 中，一个 GNN 学习用于拟合标签后验分布的表示向量。在  M-step 中，另一个 GNN 用于建模标签依赖关系。实验结果表明，GMNN 取得了优越的结果。

相关工作

考虑半监督学习中的一个图 ，其中 V 是节点的集合，E 是节点之间边的集合， 是所有节点特征的集合。已知一部分标签 ，L∈V，我们的任务是预测剩下未知的标签 ，U = V \ L。

统计关系学习（statistical relationship learning，SRL）方法以如下方式计算标签的联合概率分布：

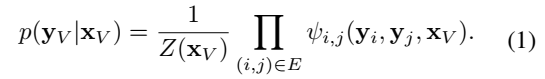
ψ 是边上的势函数，一般是人工定义的特征函数的线性组合。

这种情况下，预测未知标签任务被看做是推断问题，我们还要去计算位置标签的后验分布