turbo译码Logmap算法和sova算法

1.问题描述：

 turbo译码Logmap算法和sova算法

2.部分程序：

 

function L_all = sova(rec_s, g, L_a, ind_dec) 
% This function implememts Soft Output Viterbi Algorithm in trace back mode 
% Input: 
%       rec_s: scaled received bits. rec_s(k) = 0.5 * L_c(k) * y(k) 
%              L_c = 4 * a * Es/No, reliability value of the channel
%              y: received bits
%       g:  encoder generator matrix in binary form, g(1,:) for feedback, g(2,:) for feedforward
%       L_a: a priori information about the info. bits. Extrinsic info. from the previous
%             component decoder
%       ind_dec: index of the component decoder. 
%              =1: component decoder 1; The trellis is terminated to all zero state
%                  =2: component decoder 2; The trellis is not perfectly terminated.
% Output:
%       L_all: log ( P(x=1|y) ) / ( P(x=-1|y) )
%

% Frame size, info. + tail bits
L_total = length(L_a);
[n,K] = size(g); 
m = K - 1;
nstates = 2^m;
Infty = 1e10;

% SOVA window size. Make decision after 'delta' delay. Decide bit k when received bits
% for bit (k+delta) are processed. Trace back from (k+delta) to k. 
delta = 30;    

% Set up the trellis defined by g.
[next_out, next_state, last_out, last_state] = trellis(g);

% Initialize path metrics to -Infty
for t=1:L_total+1
   for state=1:nstates
      path_metric(state,t) = -Infty;
   end
end

% Trace forward to compute all the path metrics
path_metric(1,1) = 0;
for t=1:L_total
   y = rec_s(2*t-1:2*t);
   for state=1:nstates
      sym0 = last_out(state,1:2);
      sym1 = last_out(state,3:4);
      state0 = last_state(state,1);
      state1 = last_state(state,2);
      Mk0 = y*sym0' - L_a(t)/2 + path_metric(state0,t);
      Mk1 = y*sym1' + L_a(t)/2 + path_metric(state1,t);
      
      if Mk0>Mk1
         path_metric(state,t+1)=Mk0;
         Mdiff(state,t+1) = Mk0 - Mk1;
         prev_bit(state, t+1) = 0;
      else
         path_metric(state,t+1)=Mk1;
         Mdiff(state,t+1) = Mk1 - Mk0;
         prev_bit(state,t+1) = 1;
      end

   end
end
      
% For decoder 1, trace back from all zero state, 
% for decoder two, trace back from the most likely state
if ind_dec == 1
   mlstate(L_total+1) = 1;
else
   mlstate(L_total+1) = find( path_metric(:,L_total+1)==max(path_metric(:,L_total+1)) );
end

% Trace back to get the estimated bits, and the most likely path
for t=L_total:-1:1
   est(t) = prev_bit(mlstate(t+1),t+1);
   mlstate(t) = last_state(mlstate(t+1), est(t)+1);
end

% Find the minimum delta that corresponds to a compitition path with different info. bit estimation.       
% Give the soft output
for t=1:L_total
   llr = Infty;
   for i=0:delta
      if t+i<L_total+1
         bit = 1-est(t+i);
         temp_state = last_state(mlstate(t+i+1), bit+1);
         for j=i-1:-1:0
            bit = prev_bit(temp_state,t+j+1);
            temp_state = last_state(temp_state, bit+1);
         end
         if bit~=est(t) 
            llr = min( llr,Mdiff(mlstate(t+i+1), t+i+1) );
         end
      end
   end
   L_all(t) = (2*est(t) - 1) * llr;
end    
                  
               
      

function L_all = logmapo(rec_s,g,L_a,ind_dec)

% Log_MAP algorithm using straightforward method to compute branch metrics
% no approximation is used.
% Can be simplified to Max-Log-MAP by using approximation ln(e^x+e^y) = max(x,y).
% Input: rec_s: scaled received bits. 
%               rec_s = 0.5 * L_c * yk = ( 2 * a * rate * Eb/N0 ) * yk
%        g: code generator for the component RSC code, in binary matrix form.
%        L_a: a priori info. for the current decoder, 
%               scrambled version of extrinsic Inftyo. of the previous decoder.
%        ind_dec: index of decoder. Either 1 or 2. 
%               Encoder 1 is assumed to be terminated, while encoder 2 is open.
%
% Output: L_all: log-likelihood ratio of the symbols. Complete information.

% Total number of bits: Inftyo. + tail
L_total = length(rec_s)/2;
[n,K] = size(g); 
m = K - 1;
nstates = 2^m;          

% Set up the trellis
[next_out, next_state, last_out, last_state] = trellis(g);

Infty = 1e10;

% Initialization of Alpha
Alpha(1,1) = 0; 
Alpha(1,2:nstates) = -Infty*ones(1,nstates-1);

% Initialization of Beta
if ind_dec==1
   Beta(L_total,1) = 0;
   Beta(L_total,2:nstates) = -Infty*ones(1,nstates-1); 
elseif ind_dec==2
   Beta(L_total,1:nstates) = zeros(1,nstates);
else
   fprintf('ind_dec is limited to 1 and 2!\n');
end

% Trace forward, compute Alpha
for k = 2:L_total+1
    for state2 = 1:nstates
      gamma = -Infty*ones(1,nstates);
      gamma(last_state(state2,1)) = (-rec_s(2*k-3)+rec_s(2*k-2)*last_out(state2,2))....
           -log(1+exp(L_a(k-1)));
      gamma(last_state(state2,2)) = (rec_s(2*k-3)+rec_s(2*k-2)*last_out(state2,4))....
           +L_a(k-1)-log(1+exp(L_a(k-1)));

      if(sum(exp(gamma+Alpha(k-1,:)))<1e-300)
         Alpha(k,state2)=-Infty;
      else
         Alpha(k,state2) = log( sum( exp( gamma+Alpha(k-1,:) ) ) );  
      end   
    end
    tempmax(k) = max(Alpha(k,:));
    Alpha(k,:) = Alpha(k,:) - tempmax(k);
end     

% Trace backward, compute Beta
for k = L_total-1:-1:1
  for state1 = 1:nstates
     gamma = -Infty*ones(1,nstates);
     gamma(next_state(state1,1)) = (-rec_s(2*k+1)+rec_s(2*k+2)*next_out(state1,2))....
           -log(1+exp(L_a(k+1)));
     gamma(next_state(state1,2)) = (rec_s(2*k+1)+rec_s(2*k+2)*next_out(state1,4))....
           +L_a(k+1)-log(1+exp(L_a(k+1)));
     if(sum(exp(gamma+Beta(k+1,:)))<1e-300)
        Beta(k,state1)=-Infty;
     else
        Beta(k,state1) = log(sum(exp(gamma+Beta(k+1,:))));
     end   
  end
  Beta(k,:) = Beta(k,:) - tempmax(k+1);
end

% Compute the soft output, log-likelihood ratio of symbols in the frame
for k = 1:L_total
  for state2 = 1:nstates
     gamma0 = (-rec_s(2*k-1)+rec_s(2*k)*last_out(state2,2))....
           -log(1+exp(L_a(k)));
     gamma1 = (rec_s(2*k-1)+rec_s(2*k)*last_out(state2,4))...
           +L_a(k)-log(1+exp(L_a(k)));
     temp0(state2) = exp(gamma0 + Alpha(k,last_state(state2,1)) + Beta(k,state2));
     temp1(state2) = exp(gamma1 + Alpha(k,last_state(state2,2)) + Beta(k,state2));
  end
  L_all(k) = log(sum(temp1)) - log(sum(temp0));
end
 

        
   

 

3.仿真结论：

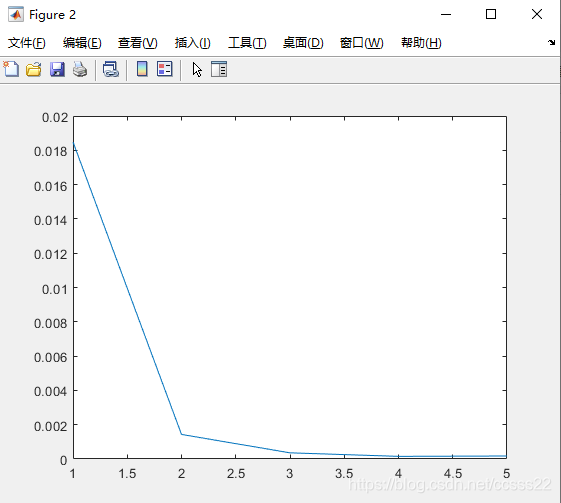
D36