时间序列分析与预测：ARIMA-LSTM综合应用股票数据

最新推荐文章于 2024-10-03 21:18:25 发布

finance褪黑素

最新推荐文章于 2024-10-03 21:18:25 发布

阅读量9.4k

点赞数 41

文章标签：人工智能机器学习深度学习

本文链接：https://blog.csdn.net/celiaweiwei/article/details/135740939

版权

ARIMA可以捕捉一些线性趋势和季节性，而LSTM可以处理更复杂的模式。ARIMA-LSTM混合模型将ARIMA和LSTM结合使用，可以提供更全面的序列建模能力，适用于既有线性趋势又有复杂非线性关系的时间序列数据。

本文提供了针对股票收盘价时间序列数据实现ARIMA-LSTM模型的Python代码，详细解释了代码每一步的思路和分析结果。

（本文没有包含具体的代码，代码文件可在gzh'finance褪黑素'下回复关键词‘240122’获取）

一、ARIMA模型拟合

使用ARIMA模型对股票数据进行拟合。ARIMA模型的拟合过程包括选择合适的阶数（p、d、q），估计模型参数，并检查模型的残差。

初始数据：

提取收盘价的变化趋势：

平稳性检验

因为p=0.143>0.05，因此需要进行差分。

为什么需要差分：

1. 统计模型通常基于一些基本的假设，其中之一是时间序列数据是平稳的。平稳性意味着时间序列的统计性质在时间上是不变的，即均值和方差是常数。非平稳性的时间序列可能会导致模型的不稳定性和不准确性。

2. 很多时间序列数据包含趋势和季节性成分，这些成分可能掩盖了数据的真实波动。通过差分，可以剥离出这些趋势和季节性因素，使得残差更接近白噪声，更适合建模。

3. 平稳时间序列的统计性质更容易建模和预测。

差分后的数据变化趋势为：

再次检验后，pvalue为2.7963374070020164e-05<0.05，因此通过平稳性检验。

白噪声检验

import statsmodels.api as sm
lb_test_stat, lb_p_value = sm.stats.acorr_ljungbox(diff1.dropna(), lags=[1], return_df=False)
print('Ljung-Box Test Statistic:', lb_test_stat)
print('Ljung-Box P-Value:', lb_p_value)

如果 lb_p_value 较大，那么可以接受白噪声假设。

自相关和偏自相关图

截尾：当时间序列的自相关函数（ACF）或偏自相关函数（PACF）在某阶之后迅速趋向于0，即不再显著，这种情况被称为截尾。对于MA模型，其自相关系数会有截尾的特性。

拖尾：与截尾相对的是拖尾，它指的是时间序列的相关函数在某阶之后仍然保持非零的值，不会突然变为零或者在接近零的地方剧烈波动。例如，对于AR模型，其偏自相关系数会有拖尾的特性。

这里自相关函数是拖尾，偏自相关为截尾，并在1步后剧降，这里应该是AR(2)模型。

使用airc和bic准确定阶，

是AR（2）模型。（ARIMA（0,1,2））

训练模型

方法一：

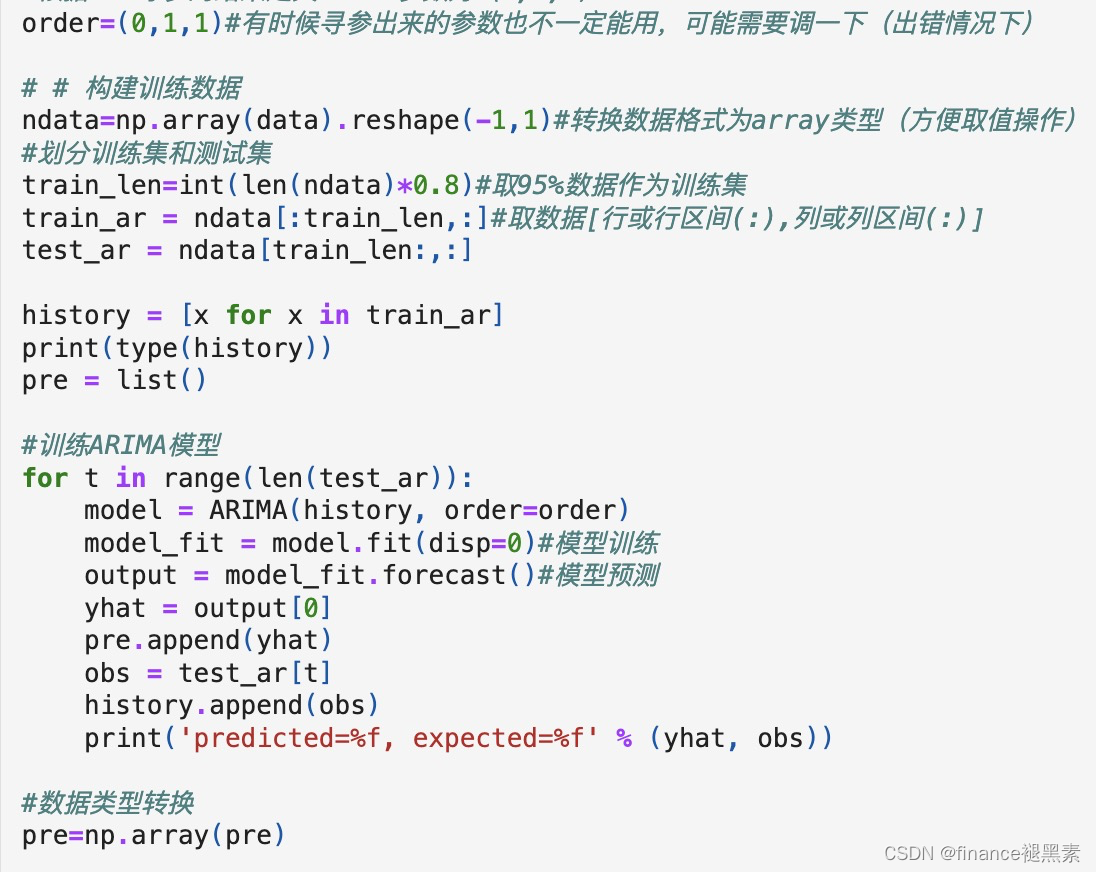
方法二：

预测结果

二、获取残差

计算ARIMA模型的残差

残差变化图形

检验残差是否为正态变化图形

为什么要检验残差是否为正态分布：

统计推断的假设： 统计推断通常基于一些假设，其中之一是残差是独立同分布的正态变量。如果残差不满足这一假设，可能会影响对参数估计、置信区间和假设检验的准确性。

模型假设检验： 检验残差是否呈正态分布有助于验证模型的基本假设。如果残差不是正态分布，可能意味着模型未能捕捉数据中的某些特征，或者存在模型的缺陷。

预测的可靠性： 在进行预测时，正态分布的残差意味着预测值的置信区间更容易计算，并且预测误差更容易解释。

模型诊断： 通过检验残差是否正态，可以进行模型的诊断。如果残差呈现出系统性的偏离正态分布的趋势，可能需要对模型进行修正或改进。

提取残差

在训练LSTM模型时，需要进行标准化或归一化处理，以确保输入数据在合理的范围内。

在训练深度学习模型，尤其是像LSTM这样的循环神经网络（RNN）时，进行标准化或归一化处理是一种常见的数据预处理。

加速收敛： 标准化或归一化可以使输入数据的分布更加接近标准正态分布，这有助于避免梯度消失或梯度爆炸的问题，从而加速模型的收敛过程。

提高梯度的稳定性： 标准化或归一化可以确保输入特征的尺度一致，这有助于使梯度在反向传播过程中更加稳定。

更好的泛化能力： 标准化或归一化可以提高模型的泛化能力，使其更适应不同尺度和范围的输入数据。