集成方法(ensemble method)
要获得好的集成,个体学习器应“好而不同”,即个体学习器要有一定的准确性(不能太坏),并且要有多样性(学习器间具有差异)。
集成方法主要可分为
个体学习器存在强依赖关系,必须串行生成的序列化方法(Boosting),
个体学习器不存在强依赖关系,可同时并行化方法(Bagging)。
- bagging 基于数据重抽样的分类器构建方法
在Bagging方法中,主要通过对训练数据集进行随机采样,以重新组合成不同的数据集,新数据集和旧数据集大小相等,利用弱学习算法对不同的新数据集进行学习,得到一系列的预测结果,对这些预测结果做平均或者投票做出最终的预测。注:随机森林算法是基于Bagging思想的机器学习算法。
- boosting
boosting和bagging很类似,但是boosting的分裂结果是基于所有分类器的加权求和结果的,每个权重代表的是对应分类器在上一轮迭代的成功度,而bagging的权重是相等的。
这族的算法工作机制蕾丝:先从初始训练集训练出一个集学习器。再根据基学习器的表现对样本分布进行调整,是的先前基学习器做错的训练样本在后续受到更多关注,然后基于调整后的样本分布训练下一个基学习器;如此反复,直到达到某个预定的足够小的错误率或达到预先指定的最大迭代次数T,最后讲这些基学习器进行加权结合。
AdaBoost算法(Adaptive Boosting)和GBDT(Gradient Boost Decision Tree,梯度提升决策树)算法是基于Boosting思想的机器学习算法。在Boosting思想中是通过对样本进行不同的赋值,对错误学习的样本的权重设置的较大,这样,在后续的学习中集中处理难学的样本,最终得到一系列的预测结果,每个预测结果有一个权重,较大的权重表示该预测效果较好。
AdaBoost算法原理
能否用弱分类器和多个实力来构建一个强分类器,前一个基本分类器分错的样本会得到加强,加权后的全体样本再次被用来训练下一个基本分类器。同时,在每一轮中加入一个新的弱分类器,直到达到某个预定的足够小的错误率或达到预先指定的最大迭代次数。
具体说来,整个Adaboost 迭代算法就3步:
- 初始化训练数据的权值分布。如果有N个样本,则每一个训练样本最开始时都被赋予相同的权重:1/N。
- 训练弱分类器。具体训练过程中,如果某个样本点已经被准确地分类,那么在构造下一个训练集中,它的权重就被降低;相反,如果某个样本点没有被准确地分类,那么它的权重就得到提高。然后,权重更新过的样本集被用于训练下一个分类器,整个训练过程如此迭代地进行下去。
- 将各个训练得到的弱分类器组合成强分类器。各个弱分类器的训练过程结束后,加大分类误差率小的弱分类器的权重,使其在最终的分类函数中起着较大的决定作用,而降低分类误差率大的弱分类器的权重,使其在最终的分类函数中起着较小的决定作用。换言之,误差率低的弱分类器在最终分类器中占的权重较大,否则较小。
算法流程
步骤1. 首先,初始化训练数据的权值分布。每一个训练样本最开始时都被赋予相同的权重:1/N。
步骤2. 进行多轮迭代,用m = 1,2, …, M表示迭代的第多少轮
a.使用具有权值分布Dm的训练数据集学习,得到基本分类器
b. 计算Gm(x)在训练数据集上的分类误差率
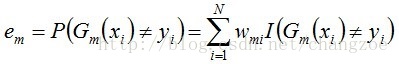

由上述式子可知,Gm(x)在训练数据集上的误差率em就是被Gm(x)误分类样本的权值之和。
c. 计算Gm(x)的系数,am表示Gm(x)在最终分类器中的重要程度(目的:得到基本分类器在最终分类器中所占的权重):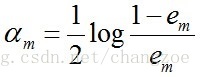
由上述式子可知,em <= 1/2时,am >= 0,且am随着em的减小而增大,意味着分类误差率越小的基本分类器在最终分类器中的作用越大。
d. 更新训练数据集的权值分布(目的:得到样本的新的权值分布),用于下一轮迭代
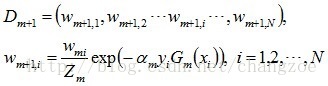
使得被基本分类器Gm(x)误分类样本的权值增大,而被正确分类样本的权值减小。就这样,通过这样的方式,AdaBoost方法能“聚焦于”那些较难分的样本上。
其中,Zm是规范化因子,使得Dm+1成为一个概率分布:
步骤3. 组合各个弱分类器
从而得到最终分类器,如下:
基于单层决策树构建弱分类器
单层决策树(decision stump)是一种简单的决策树桩
准备数据集
from numpy import *
from operator import*
import matplotlib.pyplot as plt
def loadSimpData():
datMat = matrix([[ 1. , 2.1],
[ 2. , 1.1],
[ 1.3, 1. ],
[ 1. , 1. ],
[ 2. , 1. ]])
classLabels = [1.0, 1.0, -1.0, -1.0, 1.0]
return datMat,classLabels画出来数据集的示意图:
def showScatter(matrix, labels):
plt.figure(figsize=(8,6))
x1 = []; y1 = []; x2 = []; y2 = []
for i in range(len(labels)):
if labels[i] == 1.0:
x1.append(matrix[i, 0])
y1.append(matrix[i, 1])
else:
x2.append(matrix[i, 0])
y2.append(matrix[i, 1])
plt.scatter(x1, y1, marker='o',color='g', alpha=0.7, label='1.0')
plt.scatter(x2, y2, marker='^',color='r







 本文介绍了集成学习中的Adaboost算法,包括其工作原理、弱分类器构建和权重更新过程。 AdaBoost通过迭代训练单层决策树,并根据分类误差调整样本权重,构建强分类器。文章还给出了Python实现的伪代码,并提到了在实际数据集上可能存在的过拟合问题。最后,简述了如何在sklearn库中使用AdaBoost。
本文介绍了集成学习中的Adaboost算法,包括其工作原理、弱分类器构建和权重更新过程。 AdaBoost通过迭代训练单层决策树,并根据分类误差调整样本权重,构建强分类器。文章还给出了Python实现的伪代码,并提到了在实际数据集上可能存在的过拟合问题。最后,简述了如何在sklearn库中使用AdaBoost。
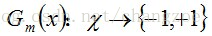
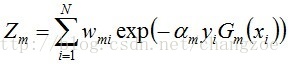
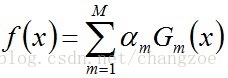
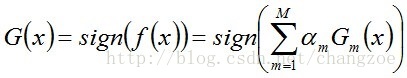
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 379
379

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








