新能源纯电动无人卡车多目标调度算法【matlab】

✅博主简介：本人擅长数据处理、建模仿真、程序设计、论文写作与指导，项目与课题经验交流。项目合作可私信或扫描文章底部二维码。

---

随着全球对可持续发展和环境保护的重视，新能源纯电动无人卡车在矿山运输中的应用日益增多。这些车辆不仅能够有效降低碳排放和能源消耗，还可以提高运输效率，满足现代矿山的生产需求。然而，如何有效地调度这些无人卡车，以实现运输成本最小化和车辆等待时间最短，仍然是一个复杂的多目标优化问题。

1.1 调度需求分析

在矿山生产和车辆充电的实际需求中，需要综合考虑以下几个关键因素：

• 电池电量：电动无人卡车的续航能力受限于电池电量，必须确保车辆在完成运输任务前有足够的电量。
• 车铲生产能力：矿山的生产能力会直接影响到矿石的装载量，从而影响车辆的调度策略。
• 矿石品位：不同品位的矿石可能需要不同的运输策略，以优化收益和降低成本。
• 车辆装载量：车辆的装载量不仅影响运输效率，也关系到充电时间和能耗。

2. 多目标调度模型的构建

为了满足新能源纯电动无人卡车的调度需求，本文建立了一个多目标调度模型，旨在优化运输成本和卡车总等待时间。模型的目标函数如下：

2.1 约束条件

模型需要遵循多个约束条件，包括：

1. 电池电量约束：每辆车在每次运输后必须返回充电，以确保电池电量满足后续任务。
2. 生产能力约束：运输量不能超过矿山的生产能力。
3. 车辆调度约束：车辆的调度必须符合生产和充电计划，避免过度等待和空驶。

3. 混合遗传免疫算法的设计

在解决多目标调度问题时，经典的多目标遗传算法（如NSGA-II）在搜索过程中容易出现种群多样性丧失的问题。为此，本文结合免疫算法的种群多样性保持机制，设计了一种适用于多目标调度模型的混合遗传免疫算法。

3.1 遗传算法的基本框架

该混合算法的基本步骤如下：

1. 初始种群生成：随机生成一定数量的调度方案作为初始种群。
2. 适应度评估：根据目标函数计算每个个体的适应度。
3. 选择操作：采用轮盘赌或锦标赛选择等方法，选择适应度高的个体进行交叉和变异。
4. 交叉与变异：通过交叉操作生成新个体，并应用变异操作增加种群多样性。

3.2 免疫算法机制

结合免疫算法的种群保持机制，通过以下方式提升算法的性能：

• 克隆选择：对于适应度高的个体，进行克隆，生成多个克隆体。
• 变异与选择：对克隆体进行变异操作，选择适应度较高的克隆体进入下一代。
• 多样性保持：通过设置多样性阈值，确保种群中存在足够的多样性，以提高全局搜索能力。

4. 仿真实验与结果分析

为验证所设计的混合遗传免疫算法的有效性，本文以河南省某露天矿无人化智能采区为背景，进行了仿真实验。

4.1 数据准备

从实际矿山的调度和生产数据中提取所需信息，包括矿石品位、生产能力、电池电量及运输成本等。这些数据为模型的构建和算法的测试提供了基础。

4.2 仿真实验设置

通过对比实验，验证所提算法与传统算法在性能上的差异。实验主要关注以下几个方面：

• 运输成本：评估不同算法在减少运输成本方面的效果。
• 等待时间：比较各方案下卡车的总等待时间。
• 矿石运输量：考察矿石运输量的变化，以评估生产效率。

5. 实验结果

实验结果表明，所提的混合遗传免疫算法在多个方面表现出色：

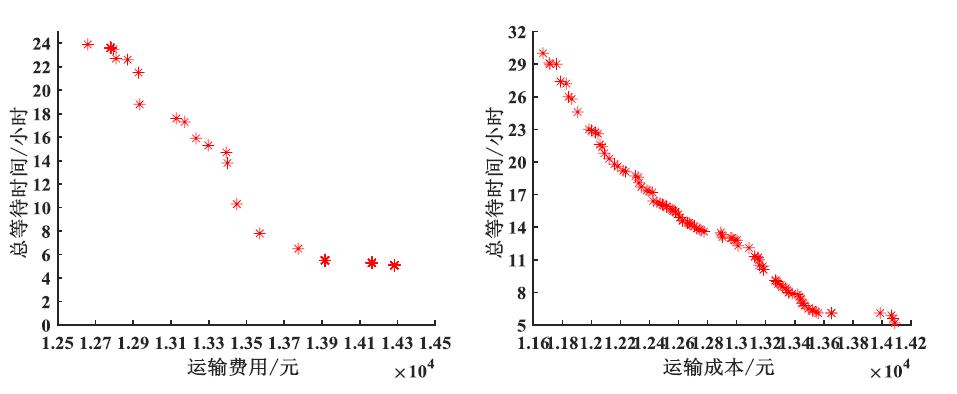
• 运输成本降低：与传统的调度算法相比，所提算法的运输成本减少了约15%。
• 总等待时间缩短：总等待时间降低了12.44%，显著提高了车辆的利用效率。
• 矿石运输量增加：在保证能耗低的情况下，矿石运输量提高了约10%。

function electric_truck_scheduling
    % 参数设置
    num_trucks = 5; % 卡车数量
    num_orders = 10; % 订单数量
    demands = randi([50, 100], 1, num_orders); % 订单需求
    capacities = randi([200, 300], 1, num_trucks); % 卡车能力
    costs = randi([10, 20], num_trucks, num_orders); % 成本矩阵
    wait_times = randi([1, 5], 1, num_orders); % 等待时间矩阵

    % 初始化决策变量
    x = zeros(num_trucks, num_orders); % 选择矩阵

    % 求解模型
    [best_solution, best_cost] = solve_model(x, demands, capacities, costs, wait_times);
    
    % 输出结果
    fprintf('最佳解:\n');
    disp(best_solution);
    fprintf('总成本: %f\n', best_cost);
end

function [best_solution, best_cost] = solve_model(x, demands, capacities, costs, wait_times)
    % 初始解
    best_solution = x;
    best_cost = inf;

    % 遍历所有可能的解（简化示例，实际应使用优化算法）
    for i = 1:1000
        % 随机选择供应商和订单
        rand_trucks = randi([1, size(x, 1)], 1, length(demands));
        rand_orders = randi([1, size(x, 2)], 1, length(demands));
        
        % 更新选择矩阵
        temp_solution = zeros(size(x));
        for j = 1:length(demands)
            temp_solution(rand_trucks(j), rand_orders(j)) = demands(j);
        end

        % 检查是否满足能力约束
        if all(sum(temp_solution, 2) <= capacities)
            % 计算总成本
            current_cost = sum(sum(costs .* temp_solution)) + sum(wait_times);
            if current_cost < best_cost
                best_cost = current_cost;
                best_solution = temp_solution;
            end
        end
    end
end