参考文档:
《统计学习方法》
目录
1: SMO 算法流程
2: SMO 推导过程
2: pytorch 例子
一 SMO(sequential minimal optimizaion)
输入:
训练数据集
其中
精度
输出:
优化过程:
1 初始值
2 选取优化变量 解析求解两个变量的最优化问题 (101-103),求得最优化问题
,求得最优解
,更新
为
3 如果精度 范围内满足停机条件,执行4
其中
否则设k=k+1,转2
4 取
二 SMO 原理推导
凸二次规划对偶问题
整个算法包含两个部分:
两个变量二次规划的解析方法 和 选择变量的启发式方法
2.1 两个变量的二次规划求解方法
2.1 约束条件
证明:
当
当
然后,需要根据本身约束再做一次剪切
2.2 最优化问题定理,未经剪切的解
经剪切后的解为
公式1
g
公式2
证明:
设
,则
求偏导数
设
带入公式1,2展开后
2.3 变量的选择方法
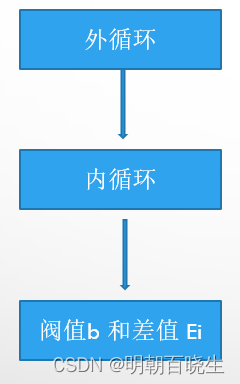
1 外循序
选取出违反KKT条件最严重的点
KKT 条件
s.t
2 内循环
目的: 希望 变化最大化
原理:
已知
则:
为了使得![]() 变化最大,就要使得
变化最大,就要使得
![]() 最大... 式1
最大... 式1
前面知道
要使得式1最大,则
![]() 必须最大
必须最大
3 : 计算阀值b 和 差值 ![]()
由KKT条件可知
3.1 ![]()
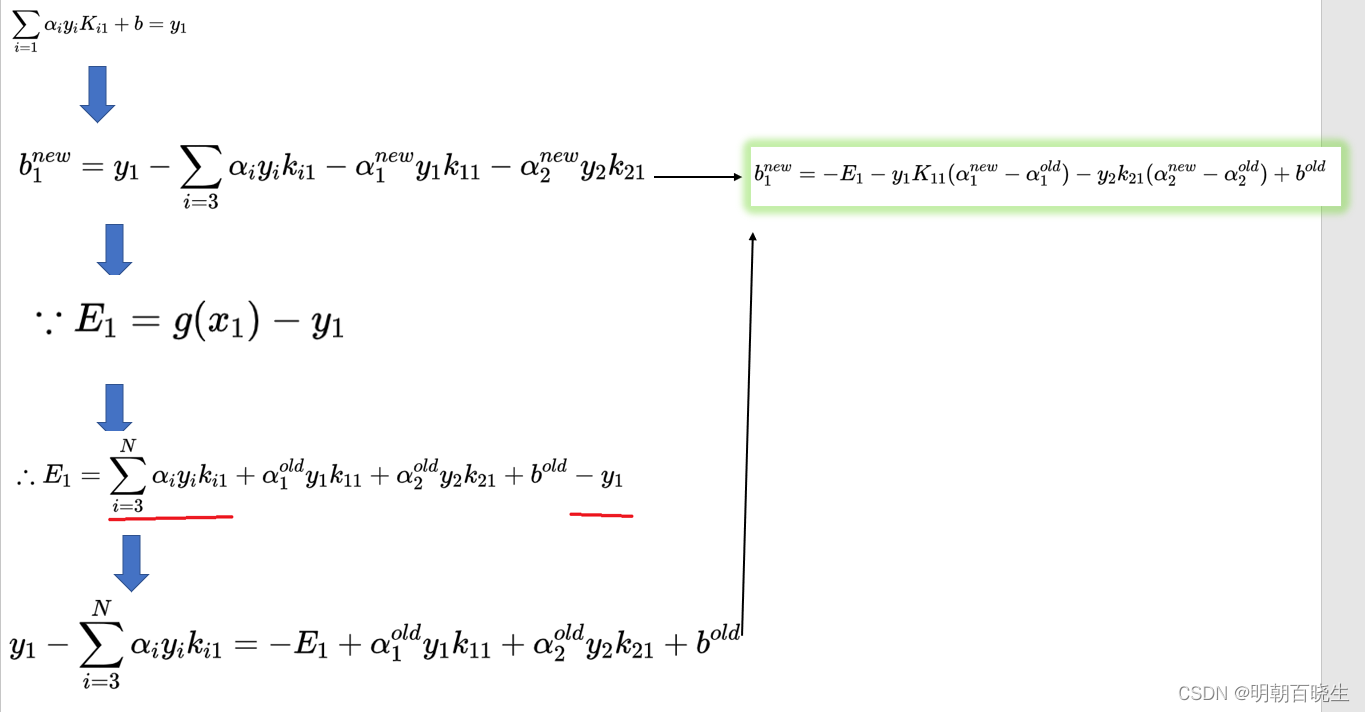
同理

![]()
如果二者都是0,或者C ,则选取它们之间的中间值






















 1432
1432











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








