基于不确定性量化的非精确概率可靠性理论

以美国圣迪亚国家实验室为代表的研究机构提出的不确定性量化(Uncertainty Quantification)方法为切入点，研究其蕴含的关键理论问题，以此为基础初步建立了一套非精确概率可靠性理论，主要包括不确定性量化快速算法、多源异类信息的统一表示与建模、认知不确定性下的可靠性分析方法、非精确概率下典型系统的可靠性评估方法、认知不确定性下的可靠性灵敏度分析方法等。

1  不确定性量化快速算法

提出了一种基于区间-遗传算法的证据理论不确定性量化方法，将系统状态方程为单调、非单调时的不确定性量化纳入到统一的算法框架中来实现，从而克服了蒙特卡洛法效率较低、顶点法无法处理非单调系统的缺点。仿真结果表明，所提出方法的计算效率明显优于顶点法和蒙特卡洛法。在信息不充分、数据不完整、存在大量不确定性的情况下，该方法可使系统性能或可靠性评估的计算量大幅下降，对于状态方程为非单调的情况，可使计算性能提升5个数量级，从而使基于证据理论的不确定性量化方法在复杂系统中的应用变得工程可实现。

表 1  算法计算效率对比

方法	目标函数区间扩张评估次数NEf	梯度函数NEf’	目标函数评估次数Nf	随机数生成次数Nrnd	计算时间/s	精度e
本文方法 J.C. Helton方法	2.05×105 -	3.26×105 -	- 9.86×1011	- 6.6×109	3.68×102 4.87×107	10-4 10-4

2  多源异类信息统一表示与建模

在复杂系统的性能、可靠性评估中，由于信息不完备、实验样本有限、对复杂物理过程的认识不充分等原因，存在多种不确定性。由于不确定性的来源不同，因此在系统建模时不确定性参数存在概率分布、模糊分布、概率包络、区间信息等多种表达方式，难以用统一的方法对系统的性能、可靠性进行量化评估。研究了概率分布、概率包络、模糊分布、专家估计信息、小样本测试数据等不同类型的信息转化为基于证据理论的统一表示的方法，讨论了基于证据理论的异类信息统一表示方法在模型不确定性量化中的应用。实例仿真表明了所提出方法的有效性。

3  认知不确定性下的可靠性分析方法

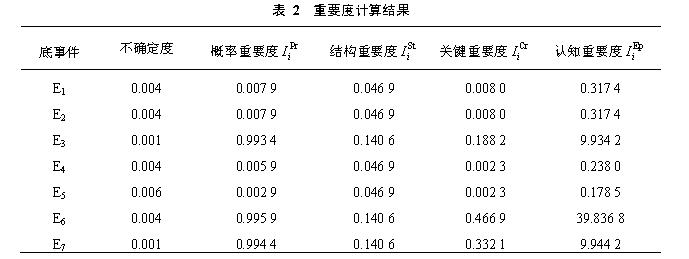
针对可靠性分析中存在的认知不确定性问题，将证据理论引入到贝叶斯网络。给出了存在认知不确定性时故障树向贝叶斯网络的转换方法，以及基于信任测度和似然测度求解顶事件发生概率的方法。研究了三种重要度的求解方法，同时提出了一个重要概念——认知重要度，给出了其实际意义和计算方法。最后，运用所提出方法对某导弹发动机进行了可靠性分析，结果表明，该方法增强了贝叶斯网络处理不确定性信息的能力，简单有效且可以得到更丰富的信息。

4  非精确概率下典型系统的可靠性评估方法

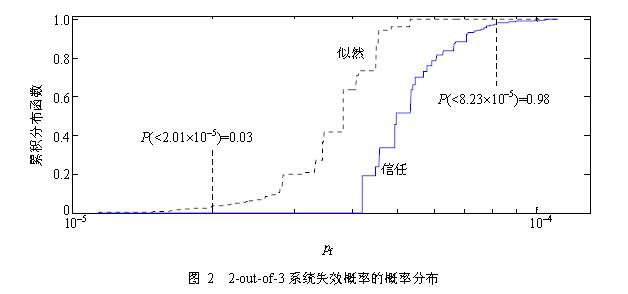
(1)当系统的各个单元的失效概率为不精确概率时，传统的概率方法难以使用，而区间分析法等非概率方法得到的结果则比较粗糙。基于证据理论，建立了非精确概率下串联、并联、串并混联、k-out-of-n等典型系统的可靠性模型，利用信任函数和似然函数并根据证据推理，将单元可靠性中的不确定性传递到顶层系统，从而得出系统失效概率和可靠度的概率分布的上下界。实例分析表明，所提出的方法能较好地处理可靠性计算中的不精确信息，且比区间分析法得到的有效信息更多。

(2)在复杂系统的可靠度计算中，由于信息不完备、实验样本有限、对复杂物理过程的认识不充分等原因，随机不确定性和认知不确定性往往同时存在，可靠度计算的复杂度大幅增加。提出了基于证据理论的可靠度近似计算方法，该方法以信任测度和似然测度的均值作为可靠度的近似值。分别讨论了系统中只含随机不确定性和同时包含随机-认知不确定性时不确定性参数离散化的方法，研究了极限状态函数为单调和非单调时信任测度和似然测度的计算方法。算例仿真表明，所提出的方法在满足计算精度的条件下计算效率远高于蒙特卡洛法，且具有广泛的适应性。

5  认知不确定性下的可靠性灵敏度分析方法

传统的可靠性灵敏度指标只考虑了随机不确定性，当系统中还存在认知不确定性时，该指标难以反映出基本变量中的认知不确定性对系统可靠性评估结果的影响程度。针对这一问题，引入概率包络来表达系统中的随机不确定性和认知不确定性，在此基础上建立了可靠性灵敏度分析的新指标——认知灵敏度系数，给出了其定义和代表的意义，并基于证据理论提出了认知灵敏度系数的计算方法。算例分析表明，认知灵敏度系数可以反映出基本变量中的认知不确定性对系统可靠性评估结果的不确定性的影响程度，从而为有针对性地提高可靠性评估结果的准确性提供依据。另外，基于证据理论的认知灵敏度系数的计算方法适用于极限状态函数为单调、非单调的系统，以及变量服从正态、非正态的系统，具有普适性。

[1]锁斌. 基于不确定性量化的非精确概率可靠性理论[A]. .中国工程物理研究院科技年报(2014年版)[C].:中国工程物理研究院科技年报编辑部,2014:4.