1sigma的精度

「Sigma」的定义是根据俄国数学家p.***.chebyshtv(1821-1894)的理论形成。

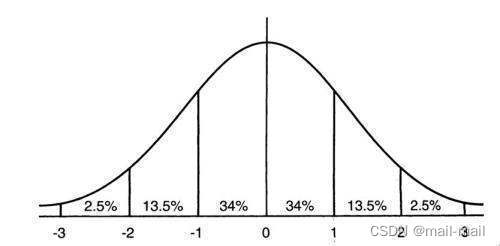
根据他的计算，如果有68.26%的合格率，便是±1Sigma（或Standard deviation,即标准方差），±2Sigma有95.44%的合格率，而±3Sigma便达至99.74%的合格率。就是正态分布的一部分。此值可参考《概率论与数理统计》第三版浙江大学盛骤，等人编P60。

标准方差（standard deviation)

就是方差的平方根：一组数据中的每一个数与这组数据的平均数的差的平方的和再除以数据的个数，取平方根既是。

即：[∑（Xn-X)^2]/n,(X表示这组数据的平均数。）

扩展资料

在统计学上的意义：

当数据分布比较分散（即数据在平均数附近波动较大）时，各个数据与平均数的差的平方和较大，方差就较大；当数据分布比较集中时，各个数据与平均数的差的平方和较小。因此方差越大，数据的波动越大；方差越小，数据的波动就越小。

样本中各数据与样本平均数的差的平方和的平均数叫做样本方差；样本方差的算术平方根叫做样本标准差。样本方差和样本标准差都是衡量一个样本波动大小的量，样本方差或样本标准差越大，样本数据的波动就越大。

方差和标准差是测算离散趋势最重要、最常用的指标。方差是各变量值与其均值离差平方的平均数，它是测算数值型数据离散程度的最重要的方法。标准差为方差的算术平方根，用S表示。