【MATLAB例程】1维状态量的自适应的CKF（容积卡尔曼滤波）代码|附代码下载链接

本文所述代码实现了一个一维容积卡尔曼滤波（CKF）算法，针对强非线性系统的状态估计问题。通过构建包含周期性驱动项和非线性饱和效应的动态模型（2.5x/(1+x²) + 8cos(1.2t)），以及非线性观测方程（x²/20），展示了CKF在无需雅可比矩阵线性化的情况下，利用确定性采样点（容积点）精确传递状态分布的能力。代码对比了滤波前后的状态误差，验证了CKF在抑制噪声和提升估计精度上的有效性。

代码介绍

初始化与动态模型

• 噪声设置：一维过程噪声协方差Q=0.01和观测噪声协方差R=1，生成对应的高斯噪声序列w和v。
• 非线性状态方程：
  X_next = X_prev + 2.5*X_prev/(1+X_prev²) + 8*cos(1.2t)
  包含非线性饱和项（2.5x/(1+x²)）和周期性驱动项（8cos(1.2t)），模拟复杂动态系统。
• 非线性观测方程：
  Z = X²/20 + v，体现状态到观测的非线性映射。

CKF算法实现

• 容积点生成：基于Cholesky分解和参数lambda=sqrt(L)（L为状态维度），生成2L个对称容积点，覆盖状态分布的均值和协方差。
• 预测步骤：
  • 容积点通过非线性状态方程传播，计算预测均值x1_mean和协方差P1_cov。
  • 叠加过程噪声协方差Q，更新预测协方差。
• 观测更新：
  • 预测观测容积点并计算均值x2_mean和协方差P2_cov。
  • 计算互协方差P3_cov和卡尔曼增益K，修正状态估计与协方差。

结果分析与可视化

• 状态对比图：显示真实值、CKF估计值与未滤波值的时序对比，直观反映滤波效果。
• 误差分析：绘制绝对误差曲线和累积分布函数（CDF），定量评估CKF的噪声抑制能力。
• 统计指标输出：输出最大误差和平均误差，验证CKF在降低估计偏差上的优势。

代码特点

1. 非线性鲁棒性：通过容积点直接传递非线性模型，避免EKF的线性化误差，尤其适用于强非线性系统（如含饱和、周期性扰动的场景）。
2. 确定性采样：基于容积规则生成固定数量的采样点（2L个），计算效率高于UKF的2L+1点，且无需调整alpha参数。
3. 数值稳定性：采用Cholesky分解确保协方差矩阵正定性，防止滤波发散。
4. 轻量化实现：一维状态简化代码结构，便于理解CKF核心流程。

改进方向

• 多维扩展：修改状态维度L，适配多自由度机械臂、多目标跟踪等场景。
• 自适应噪声协方差：引入噪声统计特性在线估计，提升对时变噪声的鲁棒性。
• 算法对比：与EKF、UKF在同一模型下对比精度与计算效率。
• 硬件部署优化：利用MATLAB Coder生成C代码，嵌入嵌入式系统实时运行。

核心公式说明

1. 容积点生成：
   KaTeX parse error: Expected 'EOF', got '_' at position 9: \text{X_̲cuba} = [\mu + …
   其中chol(P)为协方差矩阵的Cholesky分解，确保采样点对称分布。

2. 协方差更新：
   $$P_{\text{pred}}=\sum W_i(X_{\text{pred}}^{(i)}-\mu )(X_{\text{pred}}^{(i)}-\mu {)}^T+Q$$
   通过加权容积点误差更新预测协方差，叠加过程噪声影响。

该代码为理解CKF算法提供了简洁的一维实现框架，通过非线性动态与观测模型的设计，展示了其在复杂系统状态估计中的潜力。用户可通过调整噪声参数（Q、R）和动态模型，快速适配具体工程问题。

运行结果

状态量曲线（两个颜色离得近，不容易看出来区别，区别在误差图里面更明显）：

• 状态误差曲线：

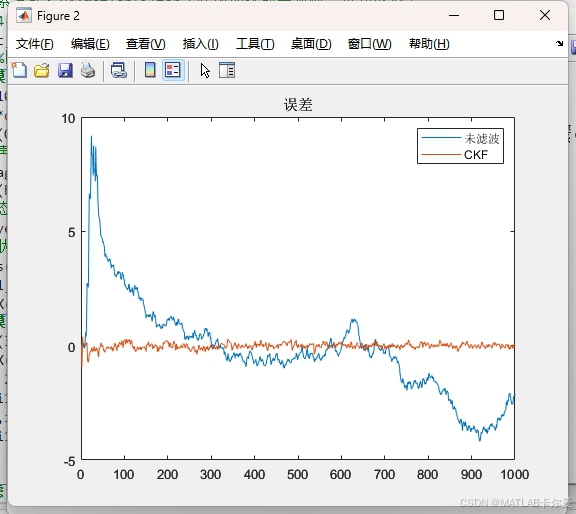
• 滤波前后CDF图像：
  

• 命令行输出结果的截图：

MATLAB源代码

部分代码如下：

% CKF的一维滤波程序例程
% 2025-04-29/Ver1
clear;clc;close all; %清空工作区、命令行，关闭小窗口
rng(0); %固定随机种子
%% 滤波模型初始化
t = 1:1:1000;% 定义时间序列
Q = 0.01*diag([1]);% 设置过程噪声协方差矩阵
w = sqrt(Q)*randn(size(Q,1),length(t)); %生成
% 观测噪声协方差矩阵和观测噪声
R = 1*diag([1]);
v = sqrt(R)*randn(size(R,1),length(t));
% 初始状态估计协方差矩阵
P0 = 1*eye(1);
% 初始化状态向量
...

完整代码下载链接：https://download.csdn.net/download/callmeup/90719233

如需帮助，或有导航、定位滤波相关的代码定制需求，请点击下方卡片联系作者