CVPR 2016
本文提出了一个快速计算大位移光流的算法。
一般的算法在 tiny structures with large motions 情况下容易出现误差。
算法采用多尺度框架,不同尺度可以提取出不同的信息。
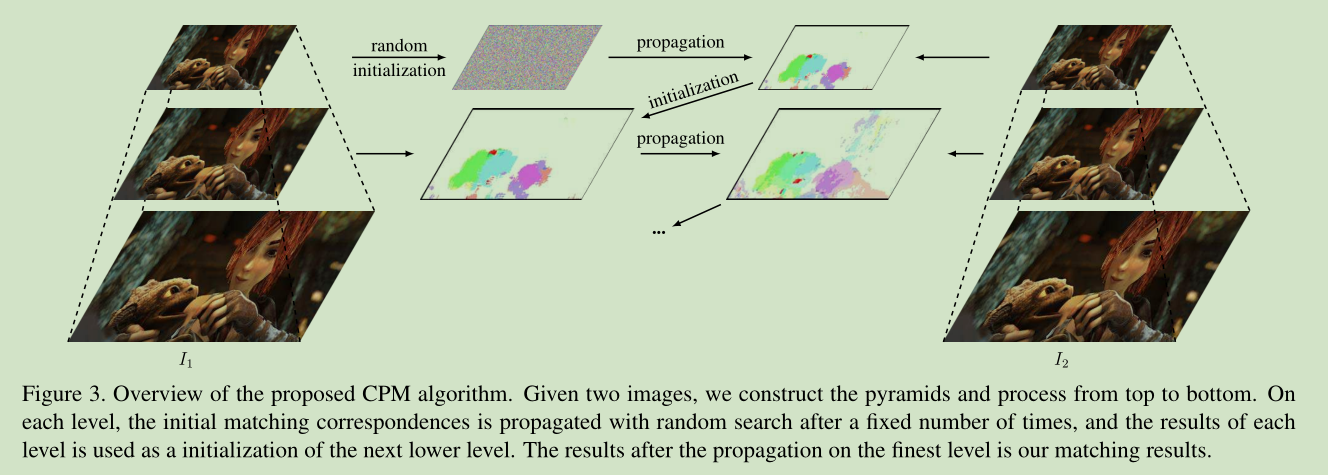
两幅图像 I1,I2,从I1里提取一系列种子点。网格提取,每个d*d区域只有一个种子点。
然后从顶层开始,建立种子点的对应关系。然后根据上层的对应关系计算下一层的对应关系。
CVPR 2016
本文提出了一个快速计算大位移光流的算法。
一般的算法在 tiny structures with large motions 情况下容易出现误差。
算法采用多尺度框架,不同尺度可以提取出不同的信息。

两幅图像 I1,I2,从I1里提取一系列种子点。网格提取,每个d*d区域只有一个种子点。
然后从顶层开始,建立种子点的对应关系。然后根据上层的对应关系计算下一层的对应关系。
 4889
4889
 2479
2479

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


