从零开始学数据分析之——《微积分》第六章多元函数微积分

最新推荐文章于 2025-04-23 17:48:22 发布

doubleyue1314

最新推荐文章于 2025-04-23 17:48:22 发布

阅读量2k

点赞数

文章标签：数据分析算法数据挖掘

本文链接：https://blog.csdn.net/doubleyue1314/article/details/126093436

版权

6.1 空间解析几何简介

6.1.1 空间直角坐标系

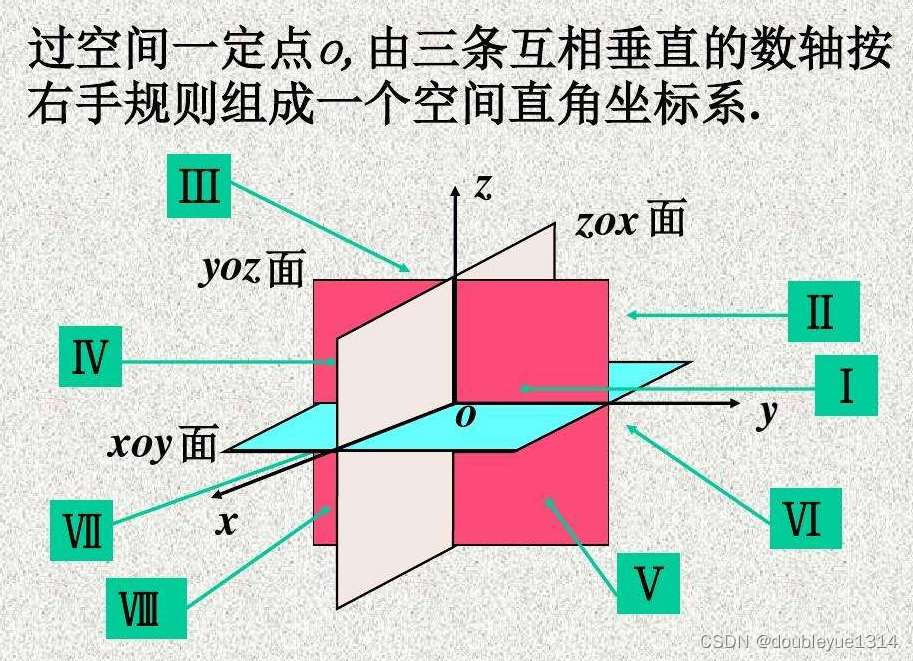
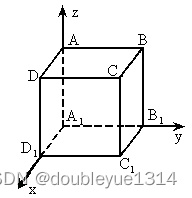
6.1.2 空间两点间的距离

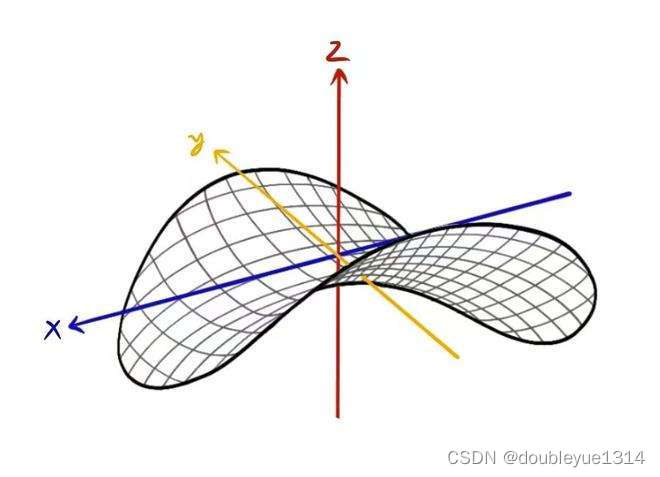
6.1.3 曲面方程

定义6.1.1 若曲面S上任意一点的坐标满足方程F(x,y,z)=0，而不在曲面S上的点的坐标都不满足方程F(x,y,z)=0，则方程F(x,y,z)=0称为曲面S的方程，而曲面S称为方程F(x,y,z)=0的图形。

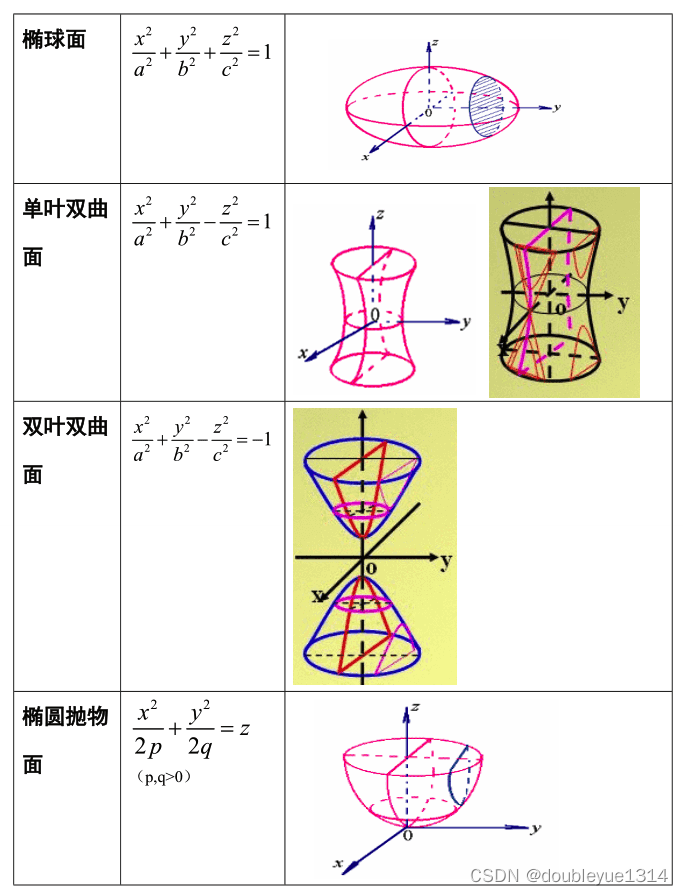
6.2 多元函数的基本概念

6.2.1 领域与平面区域

1.领域

设 $P_{0}\left ( x_{0},y_{0} \right )$ 是xOy平面上的一个点， $\delta$ 是一正数，与点 $P_{0}\left ( x_{0},y_{0} \right )$ 的距离小于 $\delta$ 的点 $P\left ( x,y \right )$ 的全体，称为点 $P_{0}$ 的 $\delta$ 邻域，记为 $U\left ( P_{0},\delta \right )$ ,即

$U\left ( P_{0},\delta \right )=\left \{ \left ( x,y \right )|\sqrt{\left ( x-x_{0} \right )^{2}+\left ( y-y_{0} \right )^{2}} \right < \delta \}$

2.平面区域

6.2.2 二元函数的概念

1.二元函数的定义

定义6.2.1 设D是一个非空的二元有序数组的集合，f为一对应法则。如果对于每一有序数组 $\left ( x,y \right )\in D$ ，都有唯一确定变量z的值与之对应，则称这个对应法则f是定义在D上的函数，或称变量z是变量x,y的二元函数，记作

$z=f\left ( x,y \right ) \left ( x,y \right )\in D$

其中x,y称为自变量，z称为因变量。集合D称为函数的定义域。

2.二元函数的几何意义

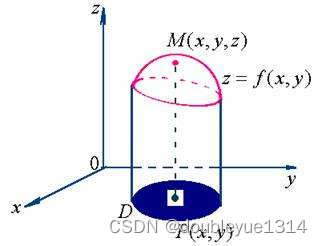
6.2.3 二元函数的极限

定义6.2.2 设函数 $z=f\left ( x,y \right )$ 在点 $P_{0}\left ( x_{0},y_{0} \right )$ 某邻域内有定义（点 $P_{0}$ 可除外），a为常数，如果对于任意给定的正数 $\varepsilon$ ，总存在一个数 $\delta$ ，使当 $0< \rho =\sqrt{\left ( x-x_{0}\right )^{2} +\left ( y-y_{0} \right )^{2}}< \delta$ 时，恒有

$\left | f\left ( x,y \right )-a \right |< \varepsilon$

成立，则称当 $\left ( x,y \right )\rightarrow \left ( x_{0},y_{0} \right )$ 时，函数 $f\left ( x,y \right )$ 以a为极限，记作

$\lim_{\left ( x,y \right )\rightarrow \left ( x_{0},y_{0} \right )}f\left ( x,y \right )=a$

为了区别于一元函数的极限，把二元函数的极限叫做二重极限。

6.2.4 二元函数的连续性

定义6.2.3 设函数 $z=f\left ( x,y \right )$ 在点 $P_{0}\left ( x_{0},y_{0} \right )$ 的某邻域内有定义，若

$\lim_{\left ( x,y \right )\rightarrow \left ( x_{0},y_{0} \right )}f\left ( x,y \right )=f\left ( x_{0},y_{0} \right )$

则称函数 $f(x,y)$ 在点 $\left ( x_{0},y_{0} \right )$ 连续，点 $\left ( x_{0},y_{0} \right )$ 叫做函数 $f(x,y)$ 的连续点。否则，称函数 $f(x,y)$

在点 $\left ( x_{0},y_{0} \right )$ 处间断，点 $\left ( x_{0},y_{0} \right )$ 叫做函数 $f(x,y)$ 的间断点。

函数 $z=f\left ( x,y \right )$ 在点 $\left ( x_{0},y_{0} \right )$ 处连续，需满足以下三个条件：

（1）函数 $f(x,y)$ 在点 $\left ( x_{0},y_{0} \right )$ 有定义

（2） $\lim_{\left ( x,y \right )\rightarrow \left ( x_{0},y_{0} \right )}f\left ( x,y \right )$ 存在

（3） $\lim_{\left ( x,y \right )\rightarrow \left ( x_{0},y_{0} \right )}f\left ( x,y \right )=f\left ( x_{0},y_{0} \right )$ .

二元函数的性质：

（1）有界性若函数 $f(x,y)$ 在有界闭区域D上连续，则 $f(x,y)$ 在D上有界

（2）最值性若函数 $f(x,y)$ 在有界闭区域上连续，则 $f(x,y)$ 在D上取得最大值和最小值

（3）界值性若函数 $f(x,y)$ 在有界闭区域上连续，m和M分别为函数 $f(x,y)$ 在D上的最小值和最大值，则对介于m和M之间的任一实数c，至少存在一点 $\left ( x_{0},y_{0} \right )\in D$ ,使 $f\left ( x_{0},y_{0} \right )=c.$

6.3 偏导数

6.3.1 偏导数

1.偏导数的定义

设函数 $z=f\left ( x,y \right )$ 在点 $\left ( x_{0},y_{0} \right )$ 的某邻域内有定义，当x从 $x_{0}$ 取得改变量 $\Delta x\left ( \Delta x\neq 0 \right ),$ 而 $y=y_{0}$ 保持不变时，函数z的改变量

最低0.47元/天解锁文章