期权二叉树估值与图计算

传统期权二叉树的算法都是基于数组的，对于没有编程基础的人来说非常不直观。二叉树是一种特殊的图，可以用python networkx这个图算法库实现，这个库不仅包含常用的图算法，还包含简单的绘图功能，非常适合研究分析使用。

def binarytree_europtionfull(S,K,r,q,sigma,t,steps,op_type):
    u=np.exp(sigma*np.sqrt(t/steps))
    d=1/u
    P=(np.exp((r-q)*t/steps)-d)/(u-d)
    
   #二叉完全树    
    G=nx.full_rary_tree(2,2**(steps+1)-1)
    G.nodes[0]['price']=S

  #正推过程
    for (parent,children) in nx.bfs_successors(G,0):

        #print(parent,children)
        G.nodes[children[0]]['price']=G.nodes[parent]['price']*d;
        G.nodes[children[1]]['price']=G.nodes[parent]['price']*u;
                
    #对最后一天到期日计算所有情况下的payoff
    for i in nx.descendants_at_distance(G,0,steps):
        G.nodes[i]['opt_val']=np.maximum(G.nodes[i]['price']-K,0)
    
    #倒推过程
    for (parent,children) in reversed(list(nx.bfs_successors(G,0))):
         G.nodes[parent]['opt_val']=((1-P)*G.nodes[children[0]]['opt_val']+(P)*G.nodes[children[1]]['opt_val'])*np.exp(-r*t/steps)    
        #print(node)
    dat=G.nodes.data()

    #生成图形显示，可注释掉。
    pos = graphviz_layout(G, prog="dot")
    nx.draw(G, pos, labels={k:"price: %.2f\n opt_val:%.2f"%(v['price'],v['opt_val']) for (k,v) in dat},with_labels=True)
    plt.show()
    
    return G.nodes[0]['opt_val']

直接用二叉树空间复杂度为，呈指数增长。我们注意到，对于中间的节点，其实有一些是相等的，因为对于一支标的价格，S*u*d=S*d*u，所以我们可以将这些节点合并，这就是网格模式。

def binarytree_europtionLattice(S,K,r,q,sigma,t,steps,op_type):
    u=np.exp(sigma*np.sqrt(t/steps))
    d=1/u
    P=(np.exp((r-q)*t/steps)-d)/(u-d)
    
    G = nx.Graph()
    G.add_node(0)
    G.nodes[0]['price']=S
    cnt=0
    for i in range(steps):
        for j in range(i+1):
            #print(j,i,cnt,cnt+i+1,cnt+i+2)
            G.add_edge(cnt,cnt+i+1)
            G.add_edge(cnt,cnt+i+2)
            cnt+=1
            
    #正推过程
    for (parent,children) in nx.bfs_successors(G,0):
        if len(children)==2:
            G.nodes[children[0]]['price']=G.nodes[parent]['price']*d;
        G.nodes[children[-1]]['price']=G.nodes[parent]['price']*u;
     #对最后一天到期日计算所有情况下的payoff，
    for i in nx.descendants_at_distance(G,0,steps):
        G.nodes[i]['opt_val']=np.maximum(G.nodes[i]['price']-K,0)
    #倒推过程
    for (parent,children) in reversed(list(nx.bfs_successors(G,0))):
         G.nodes[parent]['opt_val']=((1-P)*G.nodes[children[-1]-1]['opt_val']+(P)*G.nodes[children[-1]]['opt_val'])*np.exp(-r*t/steps)    
       
    #生成图形显示，可注释掉。
    pos = graphviz_layout(G, prog="dot")
    nx.draw(G, pos, labels={k:"price: %.2f\n opt_val:%.2f"%(v['price'],v['opt_val']) for (k,v) in dat},with_labels=True)
    plt.show()
    
    return G.nodes[0]['opt_val']

那么在这个基础上我们就可以实现美式看跌期权的二叉树定价 

def binarytree_america_lattice(S,K,r,q,sigma,t,steps):
    u=math.exp(sigma*math.sqrt(t/steps))
    d=1/u
    P=(math.exp((r-q)*t/steps)-d)/(u-d)
    
    G = nx.Graph()
    G.add_node(0)
    G.nodes[0]['price']=S
    cnt=0
    for i in range(steps):
        for j in range(i+1):
            G.add_edge(cnt,cnt+i+1)
            G.add_edge(cnt,cnt+i+2)
            cnt+=1           

    #正推过程，
    for (parent,children) in nx.bfs_successors(G,0):
        #如需查看，可注掉下行
        #print(parent,children)
        if len(children)==2:
            G.nodes[children[0]]['price']=G.nodes[parent]['price']*d;
        G.nodes[children[-1]]['price']=G.nodes[parent]['price']*u;
        
    #对最后一天到期日计算所有情况下的payoff。descendants_at_distance(G,source,distance)返回距离起点source指定距离distance所有的节点。
    for i in nx.descendants_at_distance(G,0,steps):
        G.nodes[i]['c_value']=max(K-G.nodes[i]['price'],0)
    
    #倒推过程，bfs_successors返回一个生成器，只能向下遍历，所以我们需要将其变为一个倒序的列表。
    for (parent,children) in reversed(list(nx.bfs_successors(G,0))):
    #由于广度遍历的特点，children在每层开始是两个，其他情况都是一个，这里我们使用-1下标取倒数第一个，这样总是可以取到上涨分支。而children[-1]-1总是下跌分支。        
         G.nodes[parent]['c_value']=max(((1-P)*G.nodes[children[-1]-1]['c_value']+(P)*G.nodes[children[-1]]['c_value'])*math.exp(-r*t/steps),K-G.nodes[parent]['price'])
    
    #生成图形显示，可注释掉。
    dat=G.nodes.data()
    pos = graphviz_layout(G, prog="dot")
    #price是价格，exe代表行权的payoff，c_value代表期权价格
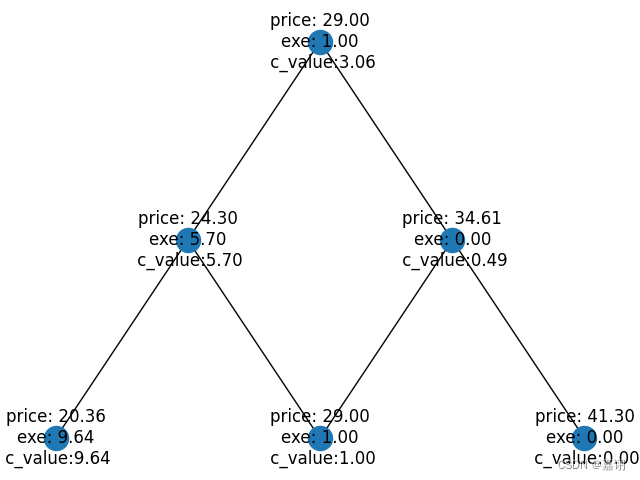
    nx.draw(G, pos, labels={k:"price: %.2f\nexe: %.2f\n c_value:%.2f"%(v['price'],max(K-v['price'],0),v['c_value']) for (k,v) in dat},with_labels=True)
    #nx.draw_networkx_labels(G, pos, labels=price)
    plt.show()
    
    return G.nodes[0]['c_value']
    
D=binarytree_america_lattice(S=29,K=30,r=0.03,q=0,sigma=0.25,t=1,steps=2)

生成的图片如下，其中exe为立即行权的payoff