诱致的解映射

诱致在我理解当中是诱导，推导的意思，即通过某个映射推导出了另一个映射
$C\in X$ 一般 $X=R^k$，C是某个博弈方混合策略的单纯形或者该博弈的混合策略集合;$\xi (t,x^0)$为微分方程经过$x^0$的解；$T(x^0)\subset R$为通过$x^0$的解得到的定义的开时间区间。
对于所有的$t\in T(x^0)$总有$x^0\in C$和$\xi (t,x^0)\in C$，且$\xi (t,x^0)$是全局的。

命题 6.1 解映射满足的条件

假设$x\subset X$开的，$\varphi :X\to R^k$是里普菲茨连续的，C是X的一个紧子集使得$\xi (t,x^0)\in C$对所有$x^0\in C$和$t\in T(x^0)$都成立，那么引致的解映射$\xi :R\times C\to C$满足以下三个条件：
$$\{\begin{array}{l}\xi (0,x)=x,\forall x\in C（6.5）\\ \xi [t,\xi (s,x)]=\xi (t+s,x),\forall x\in C,\forall s,t\in R（6.6）\\ \xi 连续（6.7）\end{array}$$
(6.5)说明，t=0时刻之后的状态等于初始状态
(6.6)说明，$\xi$经由s个时间后达到的状态，在此状态下经由t个时间单位达到的状态==经由t+s个时间单位达到的状态。
(6.6)说明，从任何固定时间t来看，通过$x^0$附近的任何初始状态$y^0$的解轨迹经过$x^0$的解轨迹。

令$D=(R,C,\xi )$是状态空间C上的一个动力系统，关键概念有如下几个：

轨迹

通过状态$x^0$的解是$\xi (\cdot ,x^0)$的图，可表示为
$\tau (x^0)=\{(t,x)\in R\times C:x=\xi (t,x^0)\}$
解映射在整个时间坐标下的像：
γ ( x 0 ) = { 对某个 t ∈ R , x ∈ C : x = ξ ( t , x 0 ) } \gamma(x^0)=\{对某个t\in R,x\in C:x=\xi(t,x^0)\} γ(x0)={对某个t∈R,x∈C:x=ξ(t,x0)}
$\gamma (x^0)$是$\tau (x^0)$到状态空间C的投影，是对整个时间坐标取状态空间的值。
解映射下非负时间轴的像：
γ + ( x 0 ) = { 对某个 t > 0 , x ∈ C : x = ξ ( t , x 0 ) } \gamma^{+}(x^0)=\{对某个t>0,x\in C:x=\xi(t,x^0)\} γ+(x0)={对某个t>0,x∈C:x=ξ(t,x0)}
存在子集$A\in C$，集合 ${\gamma }^{+}(A)$被定义为满足$x^0\in A$的所有准轨迹${\gamma }^{+}(x^0)$的并。
轨迹$\gamma$+时间变量$t$=解$\xi$

集合的不变性与前向不变性

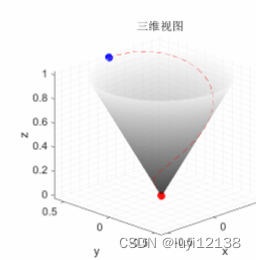
有个比较好理解的例子就是，一个小球放在圆锥里面，若给小球一个初速度，小球就会运动起来，运动轨迹唯一，最终停留在圆锥顶点处。圆锥就可以理解为一个前向不变集合，初速度就是流的大小和方向$\varphi (x)$，运动轨迹就是$\gamma (x^0)$,最终的红点就是稳态。

此处转自https://blog.csdn.net/XSTX1996/article/details/82079317

稳态

稳态就是对于实数范围内的任意时刻t都是同一个状态，也就是说状态不变，流没有大小和方向，这样状态子集是一个不变单点集，$\gamma (x)$是一个单点集。（轨迹的集合就是状态子集A）

命题6.3 极限状态的稳态

如果$x,y\in C$,并且$li{m}_{t\to \infty }\xi (t,x)=y$,那么y是稳态。

稳定性

单个状态的Lyapunovn稳定和渐进稳定

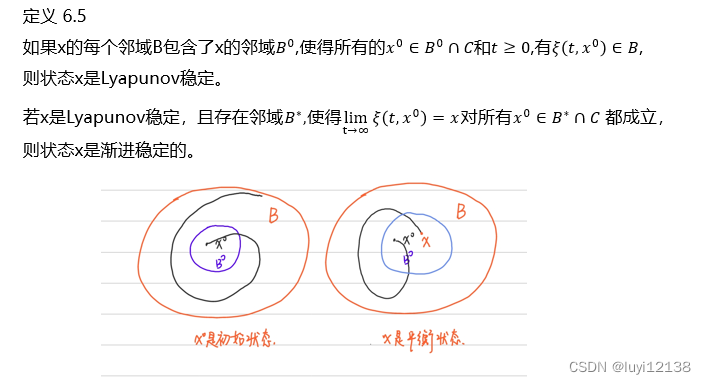
命题 6.4 如果一个状态时lyapunovn稳定的，那么它是稳态的

集合的两个稳定

单点引申到集合有如下三个概念需注意

吸引域

吸引子就相当于一个黑洞，某一个点$x^0$的轨迹绕着黑洞在转，最终趋向于集合A，这样点的集合称为A的吸引域。

本文参考《演化博弈论》乔根·W·布威尔 [著]