深度强化学习总结(DQN,DDQN,Actor-Critic,DDPG)

学习强化学习总结的笔记，按照自己的理解总结的，还没总结完，边学边总结，可能存在错误欢迎指正

1. Q值和V值

Q值：代表了智能体选择这个动作后，一直到最终状态“奖励总和”的期望；（用于衡量动作）
V值：代表了智能体在“当前状态”下，一直到最终状态的“奖励总和”的期望；（用于衡量状态）

Q值和V值的关系：

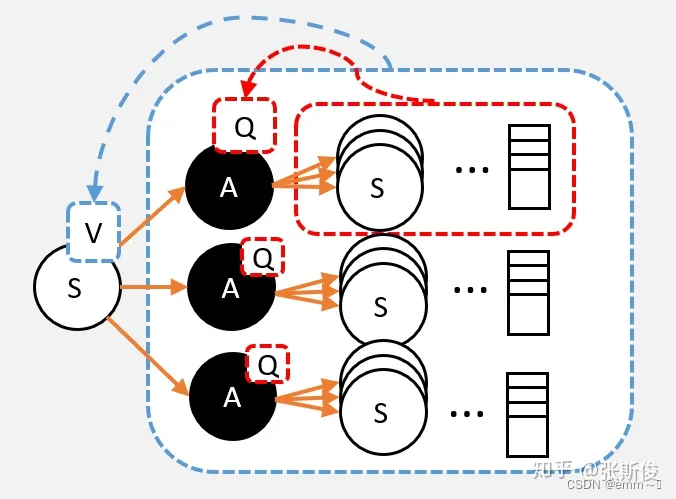
1. 基于Q计算V：一个状态的V值，就是这个状态下的所有动作的Q值，在策略下的期望，即$V_{\pi }(s)={\sum }_{a\in \mathcal{A}}\pi (a|s)\cdot Q_{\pi }(s,a)$；

![V对Q的影响](https://img-blog.csdnimg.cn/direct/63e59a70929645e1a20603d2c4799b3f.png

2. 基于V计算Q：一个动作的Q值，就是执行这个动作后所有可能状态的V值的均值，即执行动作后，状态的期望。即 $Q_{\pi }(s,a)=R_s^a+\gamma {\sum }_{s^{\prime }}{P}_{s{s}^{\prime }}^a\cdot v_{\pi }\left(s^{\prime }\right)$
3. 基于1和2，可以推出V到V的关系为
   

2. 蒙特卡洛(Monte-Carlo, MC)更新公式求V值

我们把智能体放到环境的任意状态$\mathbf{S}$；从这个状态开始按照策略进行选择动作，并进入新的状态，并一直重复该步骤直到到达最终状态${\mathbf{S}}_{end}$，并计算这一个序列的累积奖励，记为G

显然可以看出，$\mathbf{S}\to {\mathbf{S}}_{end}$有很多种情况（或者理解为路线），因此根据V的定义（智能体在“当前状态”下，一直 “走到” 最终状态的 “奖励总和” 的期望），$V_{\mathbf{s}}$可以表示为 V s = E L { G L } = 1 L ∑ l ∈ L G L V_{\mathbf{s}}=\mathbb{E}_{L}\{G_{L}\} = \frac{1}{L}\sum_{l\in L}G_{L} Vs​=EL​{ GL​}=L1​∑l∈L​GL​，L表示总路径的数量（即$\mathbf{S}\to {\mathbf{S}}_{end}$有多少种可能性）

基于上面阐述的$V_{\mathbf{s}}$的表示，若已经尝试了N种路线，且N种路线对应的 { G 1 , G 2 , . . . , G N } \{G_1, G_2,...,G_N\} { G1​,G2​,...,GN​}的均值为$V_{\mathbf{s}}$。若又有一种新的路线尝试了，即$G_{N+1}$，则$V_{\mathbf{s}}$应该更新为：
$$V_{\mathbf{s}}\leftarrow V_{\mathbf{s}}+\frac{G_{N+1}-V_{}}{N+1}$$