[图形学] 法向量变换矩阵的推导

• 在顶点着色器中, 对顶点模型空间转换到世界模型空间的矩阵用M来表示, 那么法线的变换能否直接同样用M矩阵来从模型空间(切线空间) 到世界空间呢?
• 我们知道一个4x4的变换矩阵，其平移的数据存放在第4列中即a14、a24、a34。而我们知道法线最后求得齐次形式是(x,y,z,0)，所以很明显变换矩阵的第四行和第四列都不会对法线产生影响(脑中思考下)。

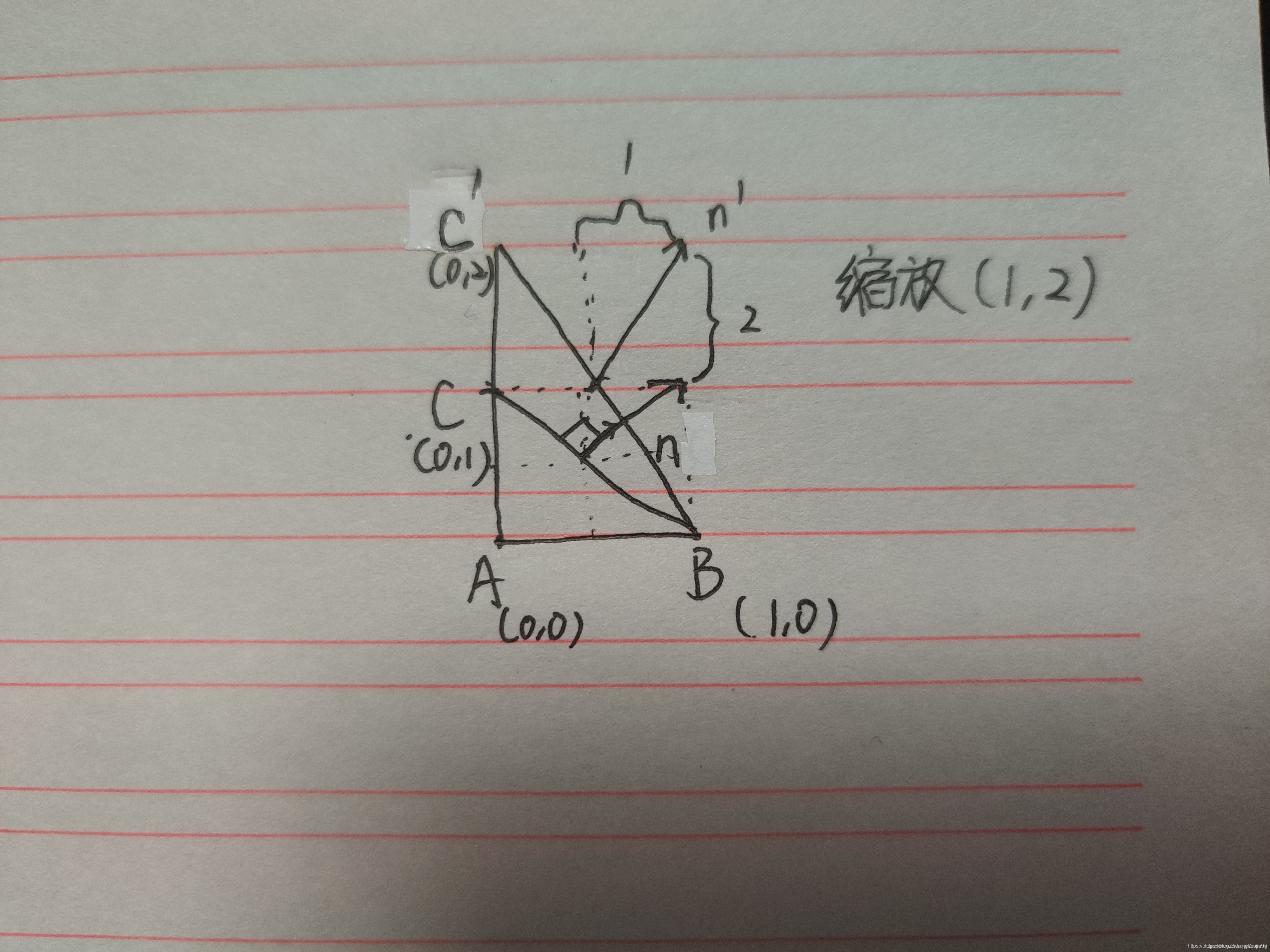
• 那我们只需要考虑变换矩阵的前3x3就行了咯。那其实就只剩旋转和缩放了，先看缩放会不会影响。如果进行非统一变换,例如:(1,2,1)，法线将不会与几何体表面垂直，大概就是下图的含义，如果要垂直，则需要其缩放的逆矩阵(2,1)即可(自行脑补下)。
  缩放(1,2):x轴不变, y轴扩大2倍

• 旋转矩阵没有影响，因为其是正交矩阵

$$\begin{gathered} X,Y是旋转前的两个切向量,U是正交矩阵 \\ X‘=U^{t}X,Y^{\prime }=U^{t}Y \\ 那么(X^{\prime }{)}^t{Y}^{\prime }=(U^{t}X{)}^t{U}^{t}Y=X^{t}U{U}^{t}Y=X^{t}Y=0 \end{gathered}$$
依然垂直.

我们大概可以确定在一些情况下，我们不能使用顶点的变换矩阵M套用至法线上。

法线变换矩阵推导过程

设切线为$t$, 法线为$n$,
可以得到$n\cdot t=n^t\cdot t=0......(1)$
设变换后的切线为$t^{\prime }$, 法线为$n^{\prime }$, 模型变换矩阵为$M$.
可以得到 $t^{\prime }=M\cdot t......(2)$ (切线是相邻量点得出的, 可以套用顶点变化矩阵)
以及 $n^{\prime }\cdot t^{\prime }=(n^{\prime }{)}^t\cdot t=0......(3)$ (变换后, 切线与法线依然垂直)
设法线的变换矩阵为S, 可以得到 $n^{\prime }=S\cdot n......(4)$
根据(2), (4) 代入(3)
$$n^{\prime }\cdot t^{\prime }=(S\cdot n{)}^{t}M\cdot t=n^t\cdot S^t\cdot M\cdot t=0$$
由于 (1), (5) 都等于0
$$n^t\cdot t=n^t\cdot S^t\cdot M\cdot t$$
等式两边, 左边* n, 右边*t^t
得到
$$S^t\cdot M=I$$
所以
$$\begin{gathered} S^t=M^{-1} \\ S=(M^{-1}{)}^t \end{gathered}$$

法线变化矩阵的用途

在光照模型中求specular 和 diffuse的时候 都需要用到法线与光照的信息.
这时候必须保证法线和光照在同一空间下,计算才意义.
光是在世界空间下的, 而法线一般存储在模型空间(切线空间), 因此必须将法线从切线空间转换到世界空间.
特别在OpenGL里
vertexSource.frag中

layout(location = 3) in vec3 aNormal; // 模型空间的法线
...
void main(){
   Normal = mat3(transpose(inverse(modelMat))) * aNormal; // 法向量需要转化成世界坐标的法向量 才能计算光照
   }