跟我一起学Multiple View Geometry多视图几何（6）

　　前言：至此我们已经讨论了Fundamental matrix的几个重要性质和基于点对x<->x’的图像关系，今天我们来学习如何从F中推导出两个相机矩阵P和P’。

9.5 推导相机矩阵

9.5.1 Projective invariance（投影不变） and canonical cameras

　　从上一篇编程实践课中我们可以清晰地感觉到，F是从x与x’的对应关系中求出来的，现在我们如果把相机移动一点，即使x与x’坐标都一起变了，算出来的F应该是一样的，所以我们就可以想到其实F与世界坐标系选择无关，比如把世界坐标系旋转后改变的只是P和P’，F不会变，所以我们断言：在三维空间的投影变换不会改变F的大小。

　　Result 9.8：如果H是三维空间里的一个4*4投影变换矩阵，那么相机矩阵P和P’所对应的Fundamental matrix和PH和P’H对应的Fundamental matrix是一样的。
证明很简单，,同理x’的也有类似形式，所以的关系就相当于。

　　所以我们知道一对相机矩阵(P,P’)唯一确定F, 而一个F确定了一组相机矩阵，这组相机矩阵可以从其中任意一组投影变换得到。

　　Result9.9：对应于一组相机矩阵P=[I | 0]和P’=[M | m]的Fundamental matrix等于，其中m是个三维向量，大家还记得中括号下标×的含义吗？如果那么。

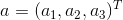
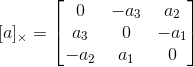
9.5.2 Projective ambiguity of cameras given F

　　我们从上面看出一个Fundamental matrix确定了一组互为投影变换的相机矩阵，下面我们会学到给定的一个Fundamental matrix所确定的一系列相机矩阵(P,P’)相当于右乘一个投影变换矩阵，因此Fundamental matrix本质上来说确定的是相机之间的投影关系。

　　Theorem 9.10：假设F是两组相机矩阵(P,P’)和(P1,P1’)对对应的同一个Fundamental matrix，那么一定存在一个非奇异4*4矩阵H满足：P1=PH, P1’=P1’H。证明略。

　　Lemma 9.11：如果一个秩为2的矩阵F可以被分解成两种：和，那么一定存在非零的a和三维向量v满足：a1=ka和。
　　我们现在把Lemma 9.11用到Theorem 9.10里面：假设P’和P1’是产生同一个F的相机矩阵，，，上下的就只需要证明这两对相机矩阵是投影相关的就行了，假设，我们就有：，进而：
　　　　　　　　　　　　　　　　　　　　　　　　
所以(P,P’)和(P1,P1’)确实是投影相关的。

　　一对相机矩阵P和P’各自含有11个自由度，总共22个自由度，为了确定一个投影空间需要15个自由度，22-15=7，这个7就是Fundamental matrix的自由度。

9.5.3 Canonical cameras given F

　　现在我们已经学习了Ｆ确定的的一系列互为投影变换的相机矩阵，我们下面推导给定Ｆ的时候推算出一堆相机矩阵的标准形式。我们先会用到下面的关于一对相机矩阵的Ｆ的描述：

　　Result 9.12：一个非零矩阵Ｆ是一对相机矩阵(P,P’)对应的Fundamental matrix的充要条件是是反对称矩阵。

　　我们从一个Fundamental matrix可以写出一对特定的相机矩阵：P=[I | 0]，P’=[SF | e’]，其中e’是epipole，所以

　　我们有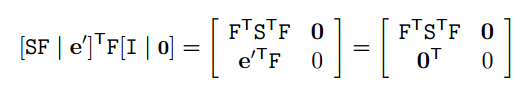：，它是反对称矩阵。

　　Result 9.14 对应于一个F的一对相机矩阵可以选择为：

　　结合上面的Theorem 9.10，我们得到如下结论：

　　对应于一个Fundamental matrix F的相机矩阵一般形式为：
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

其中：v是一个三维向量，λ是一个非零数。