几何角度理解线性代数(1):向量、线性组合、矩阵乘法、行列式
文章目录
本笔记主要基于三蓝一棕的视频进行记录。
原视频系列之一的链接为:06 - 逆矩阵、列空间与零空间_哔哩哔哩_bilibili
Take Home Me ssage
矩阵乘法与线性变换
我们可以将矩阵的列看作变换后的基向量,而将矩阵乘法看作是变换后的基向量的线性组合:
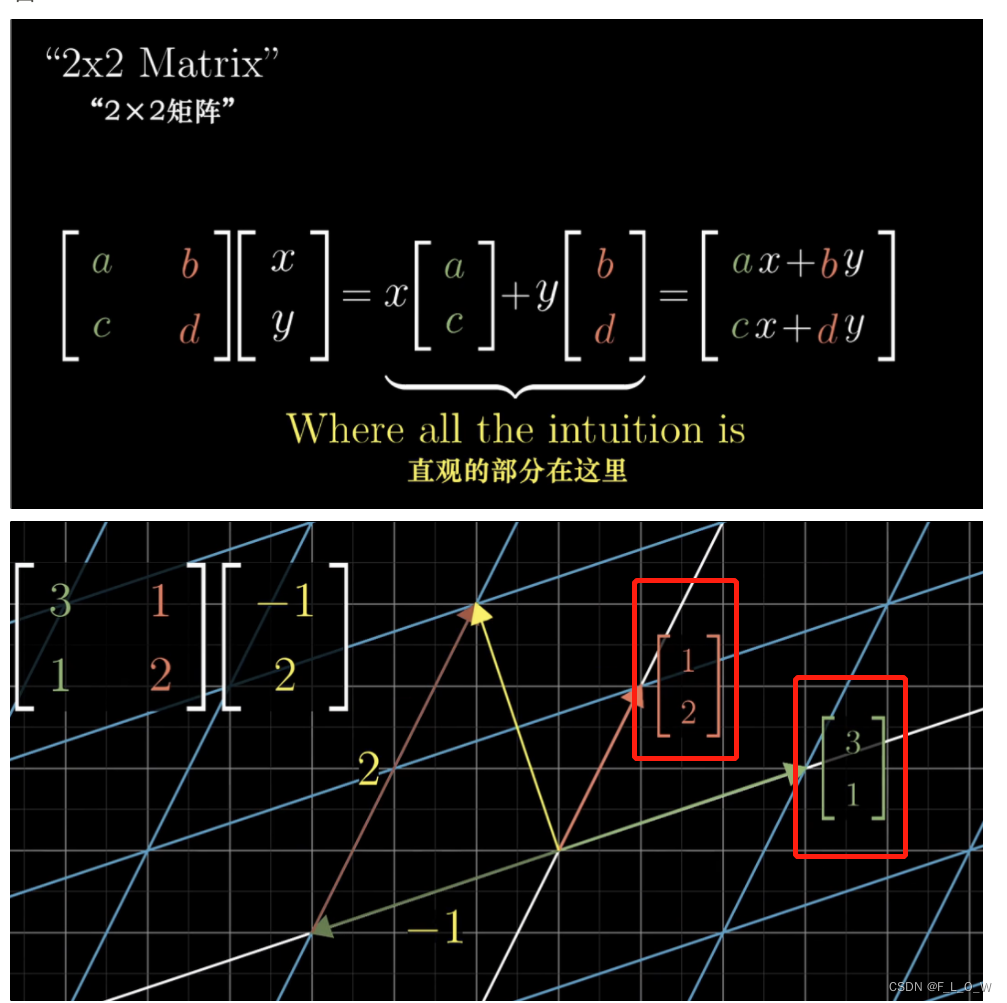
矩阵乘法与线性变换复合
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-geAtkDor-1661603012178)(https://s3-us-west-2.amazonaws.com/secure.notion-static.com/fa6a978a-f4f6-418a-8a50-868e56bef1c3/Untitled.png)]](https://img-blog.csdnimg.cn/35f9e80534dd4f1bb71ed71ab6564067.png)
行列式
行列式的几何表示:

此外,再对三维空间中行列式的几何含义,以及右手定则与左手定则进行简单的介绍:
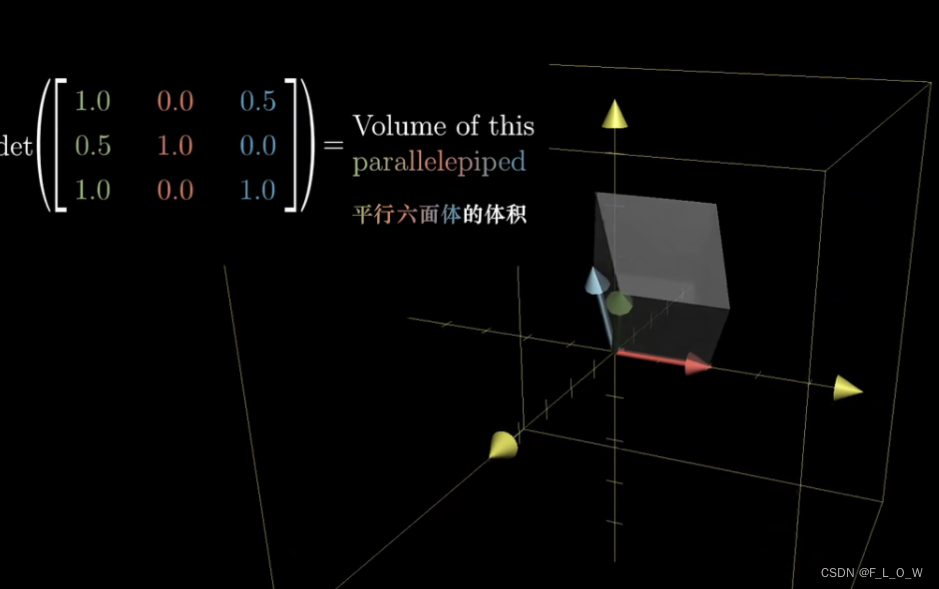
左手定则:
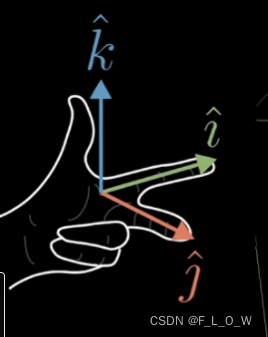
向量的基本表示
点与向量的表示:
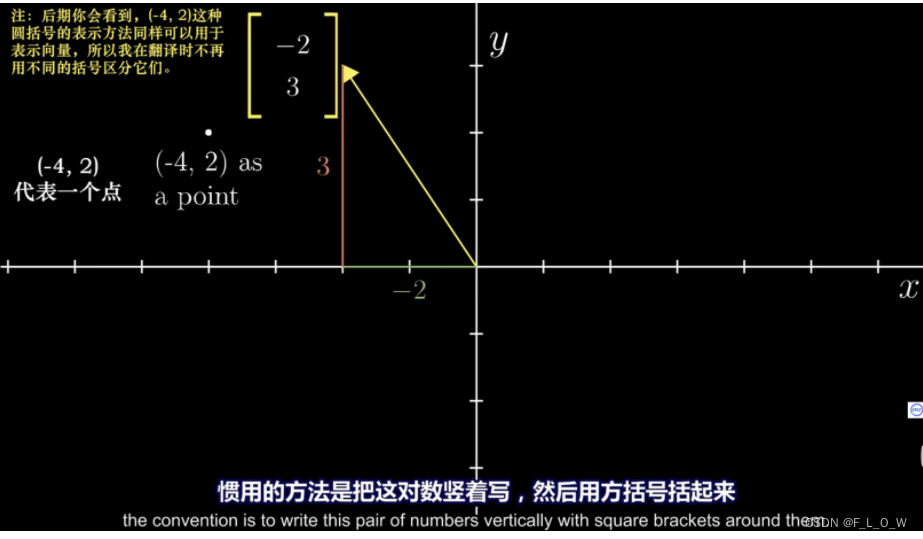
线性组合、张成的空间与基
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-6MixklDa-1661603012180)(https://s3-us-west-2.amazonaws.com/secure.notion-static.com/44645fdd-5b64-46fa-88bf-c29e798ce9f8/Untitled.png)]](https://img-blog.csdnimg.cn/ba4f744c9f374874ab21bb28e84b200c.png)

如果引入的第三个向量基恰好落在前两个向量所span成的平面中,那么意味着,第三个向量的引入,并不会使得span的空间更进一步。
而如果引入的第3个向量没有落在前两个向量所长成的空间之中,或者说平面之中。那么我们可以想象,如果固定了这个平面,而第3个向量在某一个方向上面进行缩放的话,那么相当于就是在第3个向量所表示的方向上,前两个向量所张成的平面在不停的移动。进而,这三个不共面的向量可以触及到三维空间中每一个点。也就是说这三个向量所张成的空间可以触及到三维空间中的每一个点。
我们回顾之前所提到的一种情况:如果第3个向量正好落在了前面两个向量所张成的平面上,那么意味着这个向量的加入,对于所张成的空间并无贡献。对于这种情况,我们称其为线性相关。或者说,我们可以认为这第3个向量是能够表示为前面两个向量的线性组合的,想一想为什么?答案是因为这个向量已经落在了前面两个向量所张成的空间,或者说平面之中,那么自然就可以用前面两个向量线性组合的方式进行第三个向量的表达。示意图见下:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-X7vxPHhI-1661603012181)(https://s3-us-west-2.amazonaws.com/secure.notion-static.com/9b576338-c086-4fea-abd5-5f1efe0e6c0e/Untitled.png)]](https://img-blog.csdnimg.cn/c51444bcba6c4d08b0461ae9c9a098cb.png)
那么自然,如果第3个向量的引入能够帮助所张成的空间更大一些的话,我们就称这个向量与前面两个向量是线性无关的,示意图见下:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-VmmAHtMk-1661603012182)(https://s3-us-west-2.amazonaws.com/secure.notion-static.com/18bbf500-262f-4cdf-9b17-36061f2f72f4/Untitled.png)]](https://img-blog.csdnimg.cn/6aa783efbf4f4fad9161f78319c2c055.png)
此时我们就可以给出基的基本定义:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-pBkbAeqE-1661603012182)(https://s3-us-west-2.amazonaws.com/secure.notion-static.com/84b51aed-ec30-45ac-9c5f-e28f244fdd1e/Untitled.png)]](https://img-blog.csdnimg.cn/5cc3a28b52634ffda849f006687de7b3.png)
此外,在某些数学教材中,更倾向于将三个基的线性无关定义为:

![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-tHg9SZLM-1661603012183)(https://s3-us-west-2.amazonaws.com/secure.notion-static.com/0ea33569-0be2-4487-b2a4-72d0a0a520c9/Untitled.png)]](https://img-blog.csdnimg.cn/48e1c9c329df456ab42d3e05b01a1d62.png)
矩阵与线性变换
我们首先要有一个认知,就是矩阵是作用于向量上的,那么矩阵变换相当于是”函数“一种更新潮的说法。他能够让一个输入向量,通过矩阵变换变为另外一个向量,示意图如下:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-U5YSGnoX-1661603012183)(https://s3-us-west-2.amazonaws.com/secure.notion-static.com/d060e8a9-207b-4b11-ad9a-938efde2c295/Untitled.png)]](https://img-blog.csdnimg.cn/6693ab466d6b46319239a79035427f28.png)
一种比较典型又比较简单的变换叫做线性变换。
那么线性变换,拥有着以下几个性质:
- 对于原本空间而言,直线在经过线性变换之后仍然保持为直线;
- 原点是固定的。
简单来讲可以把线性变换看作是保持网格线平行且等距分布的变化:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-CfFqDyxg-1661603012183)(https://s3-us-west-2.amazonaws.com/secure.notion-static.com/35f1e452-b5be-427b-b93c-ac6e1bb2e732/Untitled.png)]](https://img-blog.csdnimg.cn/c90bbb3f31f54deea14dc04b71f8414b.png)
接下来我们思考一下如何用数值来描述这种线性变化:

实际上我们只要记住 i i i方向的单位向量,以及 j j j方向的单位向量经过这种变换之后所在的位置,就可以进而得到所有向量在经过这种线性变换之后得到的结果。为什么这么说呢?是因为如果经过了线性变换的话,原先的向量是怎样的原先的基的线性组合,那么变换之后仍然是变换后的基的线性组合,而变换前后,这线性组合中的标量系数是一致的:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-5zQzAZa9-1661603012184)(https://s3-us-west-2.amazonaws.com/secure.notion-static.com/4900d9e0-f4c7-4896-9dfd-6872234ece1a/Untitled.png)]](https://img-blog.csdnimg.cn/992d08c266d0450fa31c0ab8bdf270df.png)
此时,线性变换的数值表示为:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-i0k8Qies-1661603012184)(https://s3-us-west-2.amazonaws.com/secure.notion-static.com/cba886ab-1793-49fe-8710-71baf2bd1d3f/Untitled.png)]](https://img-blog.csdnimg.cn/9868780ddd8c4f84b00fc7ee758f2ff3.png)
更为通用的表示为:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-kL4opWD3-1661603012184)(https://s3-us-west-2.amazonaws.com/secure.notion-static.com/3af6e28f-4d83-4cd0-91dc-0c6209289f94/Untitled.png)]](https://img-blog.csdnimg.cn/26ddc75c5b03458faa1ae15839cc2caa.png)
总之,我们可以将矩阵的列看作变换后的基向量,而将矩阵乘法看作是变换后的基向量的线性组合:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-l5tWCVrr-1661603012184)(https://s3-us-west-2.amazonaws.com/secure.notion-static.com/4f054615-1860-460e-97b9-678459975aa4/Untitled.png)]](https://img-blog.csdnimg.cn/0c6955bb4a1d415c8da770ad5f2100ea.png)
此外还有一个有意思的现象,就是如果变换后的基向量是线性相关的,那么变换后所张成的空间也就变成了一条直线:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ER67lZ30-1661603012185)(https://s3-us-west-2.amazonaws.com/secure.notion-static.com/c7fbd690-2491-4ee1-be06-b9720bd10cc5/Untitled.png)]](https://img-blog.csdnimg.cn/e370e11c63f24d6b8f97683085b280fb.png)
矩阵乘法与线性复合变换
复合变化可以直观的表示为:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-7rRbOpuM-1661603012185)(https://s3-us-west-2.amazonaws.com/secure.notion-static.com/42d86f9b-6d68-4a67-bb00-2d96462184cd/Untitled.png)]](https://img-blog.csdnimg.cn/755a285998164029aa2d91ff915dae7a.png)
需要注意的是,矩阵需要从右往左读:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-GQbbtAiY-1661603012186)(https://s3-us-west-2.amazonaws.com/secure.notion-static.com/188bf7a1-e2f8-4c8a-aa66-16a690c27998/Untitled.png)]](https://img-blog.csdnimg.cn/f9f1261739f341e18247c88c5a921e25.png)
在思考通用数值表达的过程中,一种直观的思路是考虑挨i方向上的基向量与J方向的基向量是如何变换的:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-fqXGyY8q-1661603012186)(https://s3-us-west-2.amazonaws.com/secure.notion-static.com/76a5b0da-ebb4-4e2a-a676-64a12e6ddefa/Untitled.png)]](https://img-blog.csdnimg.cn/19598c872df04ca6bc5ba7752763c872.png)
那么在三维空间,复合线性变换可以表示为:
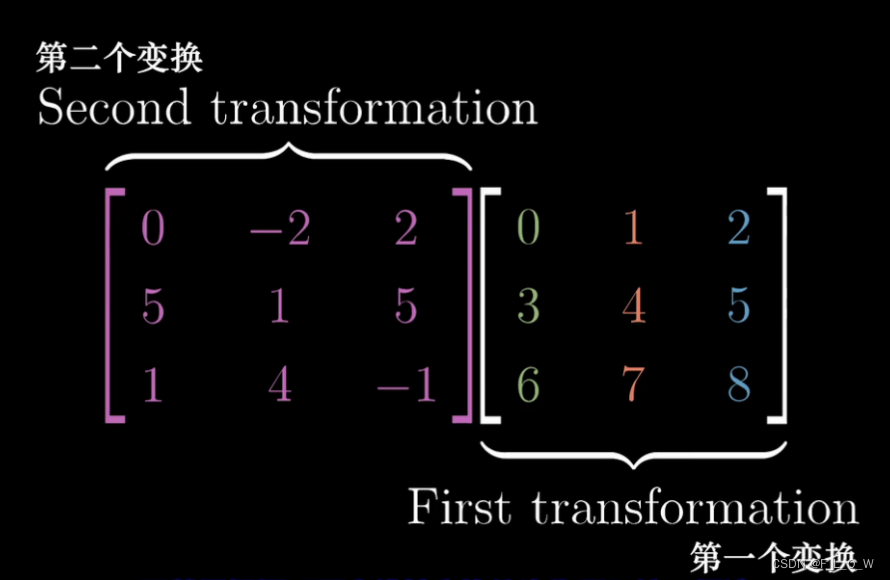
行列式
仍然从二维的角度来看,行列式在几何上直观的感受是基组合所包围的面积,即:

一种特殊情况是:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Lifivggk-1661603012186)(https://s3-us-west-2.amazonaws.com/secure.notion-static.com/7c5a0b57-0f69-40ce-a1f0-7a954cb043ad/Untitled.png)]](https://img-blog.csdnimg.cn/01c7ed04a243454a968c1d8a27386b31.png)
如果行列式的值出现了负数,通常代表着变换的基的相对方向产生了改变,比如说在变化之前i方向的基在j方向的基的右边,那么变换之后,如果i方向的基在j方向的基的左边的话,变换矩阵的行列式的值就会变成一个负值。直观上来想,可以想象成是一个平面进行了翻转。注意,即使是负值,行列式的值仍然代表着区域面积的缩放比例。
直观上来看,行列式的值,或者说面积,会在基随着下图中红色箭头的示意图进行变化的时候,慢慢从正数变到负数:
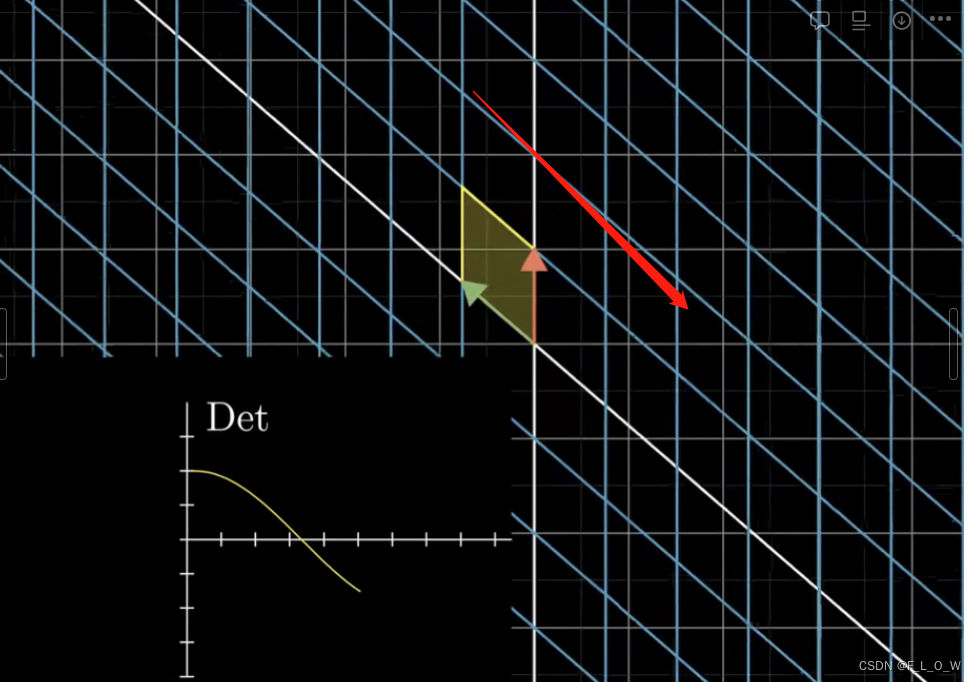
行列式的几何直观感受,扩展到三维情况之后,有: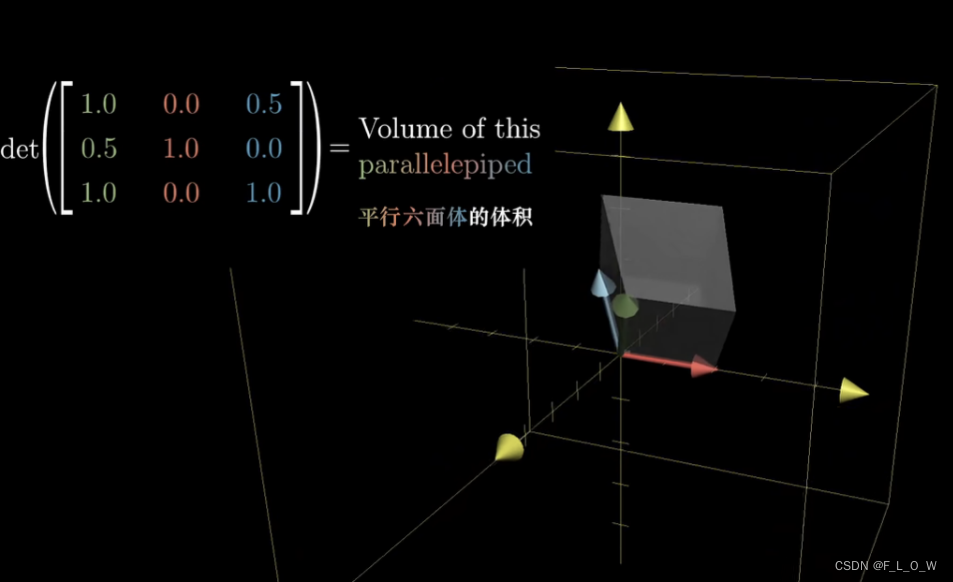
同时,对于三维空间变换时,如果行列式出现了负值,就表示三维基坐标,我们无法使用右手定则来表示。
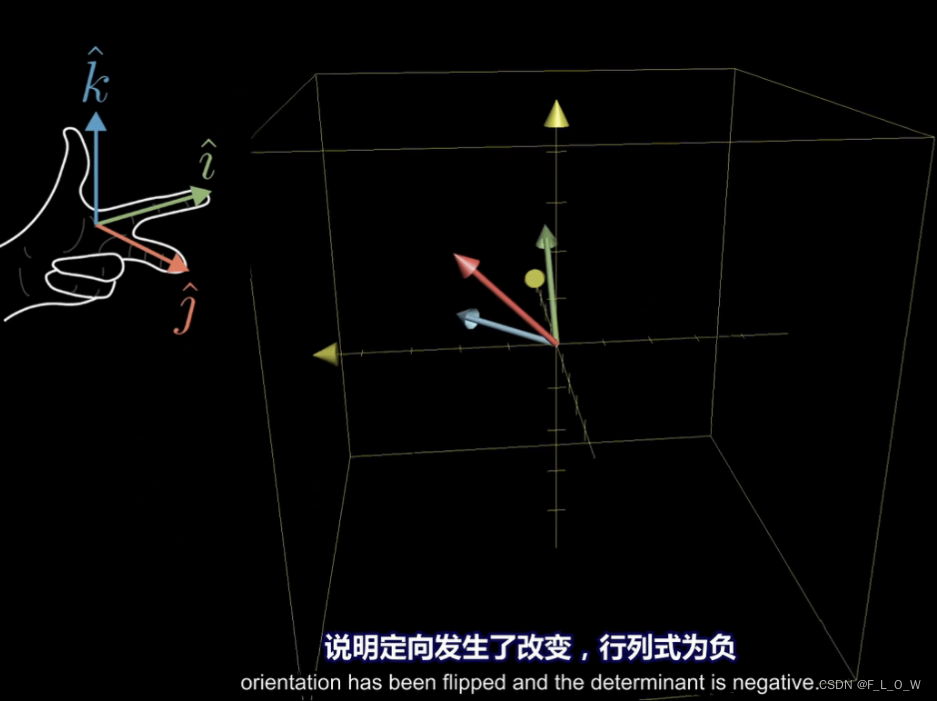
行列式的数值计算方式和几何含义分别是
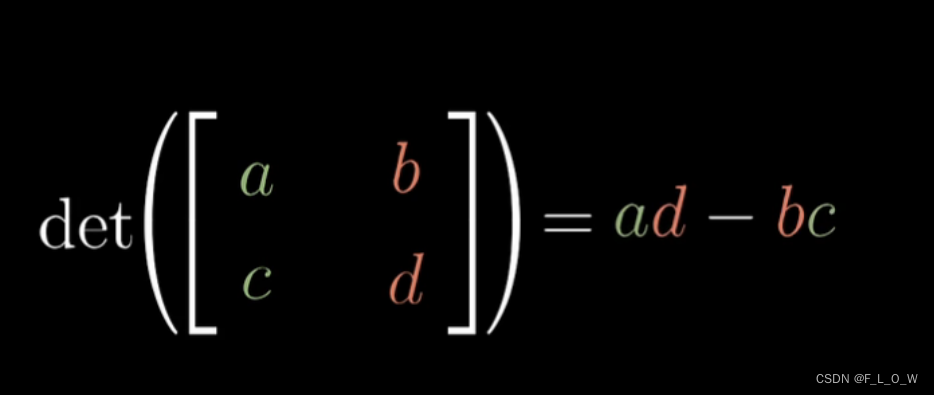
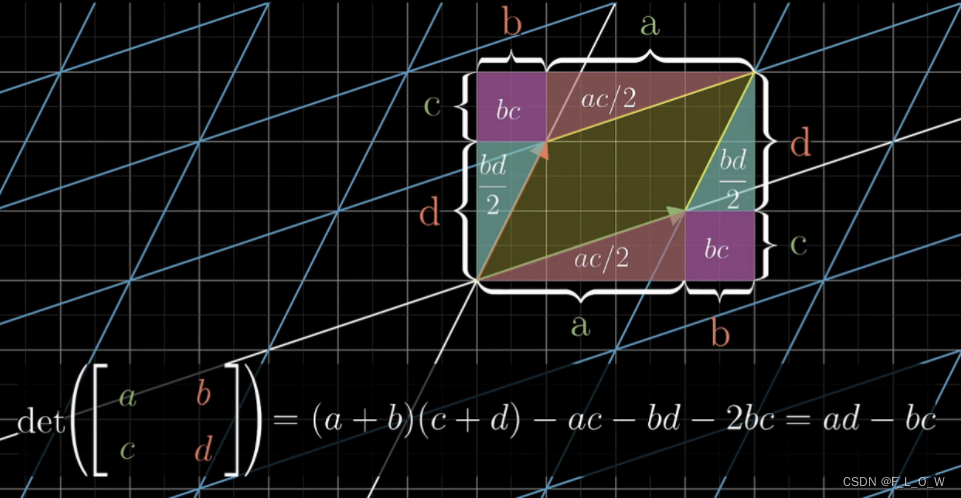
扩展到三维的矩阵计算方式是:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-XjymEPAK-1661603012187)(https://s3-us-west-2.amazonaws.com/secure.notion-static.com/d1242e99-53bf-4908-81dd-385278950d11/Untitled.png)]](https://img-blog.csdnimg.cn/08f74a852c4c47bebd9b35fea123a08f.png)
此外,关于行列式的一条有用的性质是: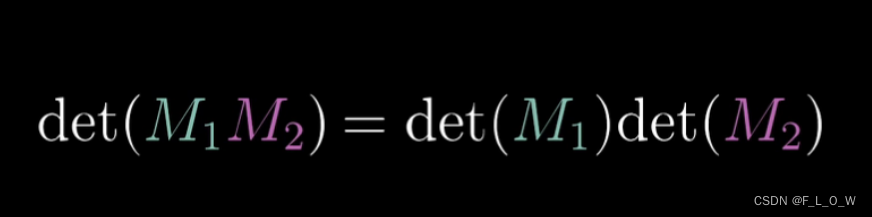
























 1098
1098











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










